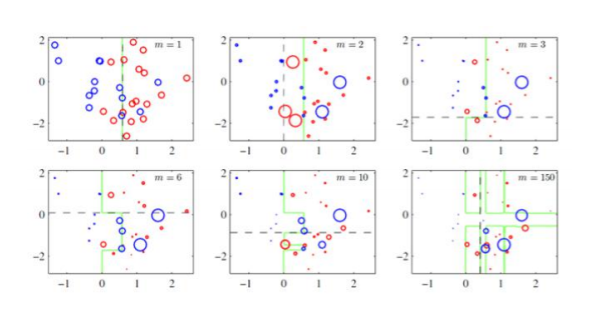
先记住这个图:

整个迭代过程直到错误率足够小或者达到一定的迭代次数为止。
分类
首先看一下原来的论文上的伪代码:

Adaboost算法将基分类器的线性组合作为强分类器,同时给分类误差率较小的基本分类器以大的权重值,给分类误差率较大的基分类器以小的权重值;构建的线性组合为:
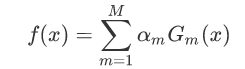
最终分类器是在线性组合的基础上进行Sign函数转换:
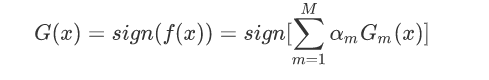
因为G(x)是经过sign化的所以得出的值是-1或1,这时候损失函数自然就是那些被分类错误的样本平均个数了:
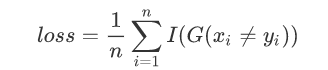
对于这样一个损失函数难以进行求导,所以这里使用下面这个函数代替:
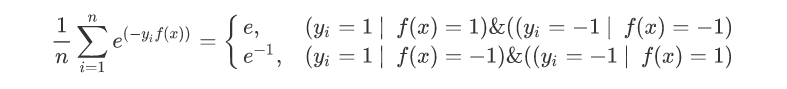
In [1]: import numpy as np
In [2]: np.exp(1)Out[2]: 2.718281828459045
In [3]: 1/np.exp(1)Out[3]: 0.36787944117144233
所以损失函数可以改变为:
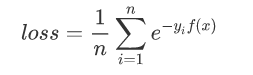
根据刚开始的图示我们可以得出:
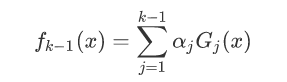
由于这里每个模型都是上一个模型得来的:
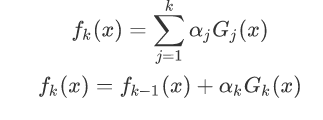
将fk(x)带入到损失函数中:
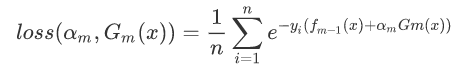
剩下的就是走机器学习的老套路求导求值,这时候就先构造参数:
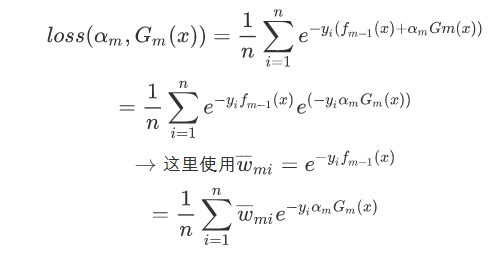
使下列公式达到最小值的αm和Gm就是AdaBoost算法的最终求解值。
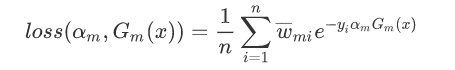
G这个分类器在训练的过程中,是为了让误差率最小,所以可以认为G越小其实就是误差率越小。
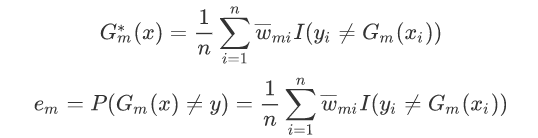
对于αm而言,通过求导然后令导数为零,可以得到公式(log对象可以以e为底也可以以2为底):
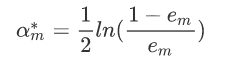
举个栗子
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| x | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| y | 1 | 1 | 1 | -1 | -1 | -1 | 1 | 1 | 1 | -1 |
x是特征,y是标签,令权值分布
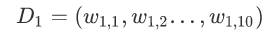
在这里:
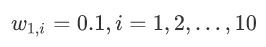
在权值分布为D1的训练数据中,当阀值为2.5的时候,误差率最低,所以这时候的基本分类器为:
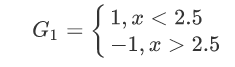
G1(x)在训练数据集上的误差率:

计算模型G1的系数:

更新数据集的权值分布:
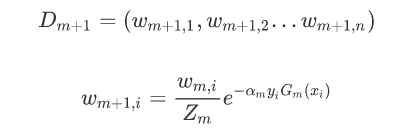
注意这里的Zm是为了归一化:

更新后的结果:
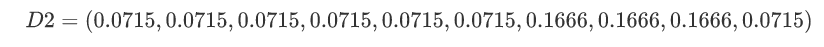
D2中分类正确的样本权值减小,错误分类的样本权值提高。
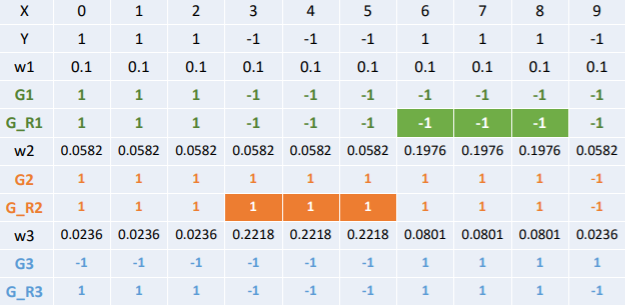
然后利用D2在训练样本中寻找误差率最低的基本分类器,在继续进行迭代。
......(这里再循环两次)
得到:

所以将新的函数f(x),放入sign()分类器中,从而输出结果:
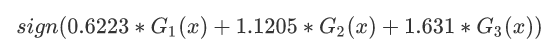
分类器sign(f3(x))在训练数据集上有0个误分类点;结束循环。
而在实际应用中我们还会添加一个缩减系数:
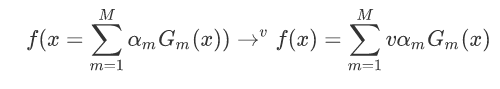
优点:
可以处理连续值和离散值;模型的鲁棒性比较强;解释强,结构简单。
缺点:
对异常样本敏感,异常样本可能会在迭代过程中获得较高的权重值,最终影响模型效果
实现代码:
import pandas as pd import numpy as np import math df = pd.DataFrame([[0,1],[1,1],[2,1],[3,-1],[4,-1], [5,-1],[6,1],[7,1],[8,1],[9,-1]]) w =np.ones(df.shape[0])/df.shape[0] #初始化权值分布 from sklearn.tree import DecisionTreeClassifier X = df.iloc[:,[0]] Y = df.iloc[:,[-1]] model = DecisionTreeClassifier(max_depth=1).fit(X,Y,sample_weight=w) ##训练第1个模型 model1 = model # print(w) # print(w * model.predict(X)) # print(Y.values.T[0]) # print(model.predict(X) != Y.values.T[0]) e = sum(w*(model.predict(X) != Y.values.T[0])) #误差率 # print(e) #0.30000000000000004 a = 1/2*math.log((1-e)/e) #学习器系数 # print(a) a1 = a z = sum(w*np.exp(-1*a*Y.values.T[0]*model.predict(X))) #规范因子 w = w/z*np.exp(-1*a*Y.values.T[0]*model.predict(X))#更新权值分布 model = DecisionTreeClassifier(max_depth=1).fit(X,Y,sample_weight=w)##训练第2个模型 model2 = model e = sum(w*(model.predict(X) != Y.values.T[0])) a = 1/2*math.log((1-e)/e) a2 = a z = sum(w*np.exp(-1*a*Y.values.T[0]*model.predict(X))) w = w/z*np.exp(-1*a*Y.values.T[0]*model.predict(X)) model = DecisionTreeClassifier(max_depth=1).fit(X,Y,sample_weight=w)##训练第3个模型 model3 = model e = sum(w*(model.predict(X) != Y.values.T[0])) a = 1/2*math.log((1-e)/e) a3 = a y_ = np.sign(a1*model1.predict(X)+a2*model2.predict(X)+a3*model3.predict(X))##模型组合 print(y_)
最后实在不懂boosting是怎么回事的,就看一下下面的图: