决策树分为两大类:分类树和回归树,前者用于分类标签值,后者用于预测连续值,常用算法有ID3、C4.5、CART等。
信息熵
信息量:
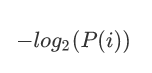
信息熵:
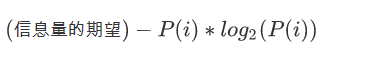
信息增益
当计算出各个特征属性的量化纯度值后使用信息增益度来选择出当前数据集的分割特征属性;如果信息增益度的值越大,表示在该特征属性上会损失的纯度越大 ,那么该属性就越应该在决策树的上层,计算公式为:

Gain为A为特征对训练数据集D的信息增益,它为集合D的经验熵H(D)与特征A给定条件下D的经验条件熵H(D|A)之差。
ID3
ID3算法是决策树的一个经典的构造算法,内部使用信息熵以及信息增益来进行构建;每次迭代选择信息增益最大的特征属性作为分割属性。
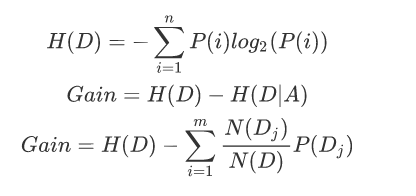
优点:
决策树构建速度快;实现简单;
缺点:
计算依赖于特征数目较多的特征,而属性值最多的属性并不一定最优ID3算法不是递增算法ID3算法是单变量决策树,对于特征属性之间的关系不会考虑抗噪性差只适合小规模数据集,需要将数据放到内存中
C4.5
在ID3算法的基础上,进行算法优化提出的一种算法(C4.5);现在C4.5已经是特别经典的一种决策树构造算法;使用信息增益率来取代ID3算法中的信息增益,在树的构造过程中会进行剪枝操作进行优化;能够自动完成对连续属性的离散化处理;C4.5算法在选中分割属性的时候选择信息增益率最大的属性,涉及到的公式为:
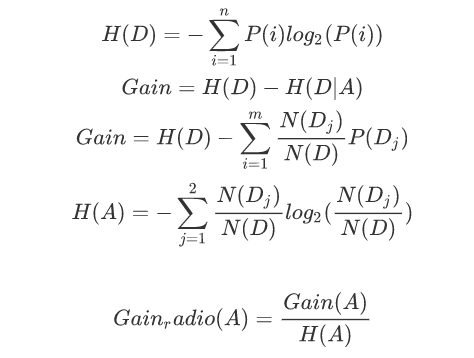
优点:
产生的规则易于理解准确率较高实现简单
缺点:
对数据集需要进行多次顺序扫描和排序,所以效率较低只适合小规模数据集,需要将数据放到内存中
CART
使用基尼系数作为数据纯度的量化指标来构建的决策树算法就叫做CART(Classification And Regression Tree,分类回归树)算法。CART算法使用GINI增益作为分割属性选择的标准,选择GINI增益最大的作为当前数据集的分割属性;可用于分类和回归两类问题。强调备注:CART构建是二叉树。
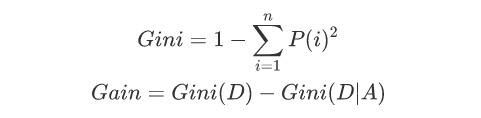
-
ID3和C4.5算法均只适合在小规模数据集上使用
-
ID3和C4.5算法都是单变量决策树
-
当属性值取值比较多的时候,最好考虑C4.5算法,ID3得出的效果会比较差
-
决策树分类一般情况只适合小数据量的情况(数据可以放内存)
-
CART算法是三种算法中最常用的一种决策树构建算法。
-
三种算法的区别仅仅只是对于当前树的评价标准不同而已,ID3使用信息增益、
-
C4.5使用信息增益率、CART使用基尼系数。
-
CART算法构建的一定是二叉树,ID3和C4.5构建的不一定是二叉树。
案例
