一、动态查找的概念:
动态查找表:表结构在查找过程中动态生成。
要求:对于给定值key, 若表中存在其关键字等于key的记录,则查找成功返回(或者删除之);否则插入关键字等于key 的记录。
二、动态查找表
- 1. 二叉排序树的定义
二叉排序树的定义(Binary Sort Tree或Binary Search Tree):二叉排序树或者是一棵空树,或者是满足下列性质的二叉树:
(1)若左子树不为空,则左子树上的所有结点的值(关键字)都小于根节点的值;
(2)若右子树不为空,则右子树上的所有结点的值(关键字)都大于根节点的值;
(3)左、右子树都分别为二叉排序树。
如下图15-1所示,该图中的树就是一棵二叉排序树。任何一个非叶子结点的左子树上的结点值都小于根结点,右子树上的结点值都大于根结点的值。
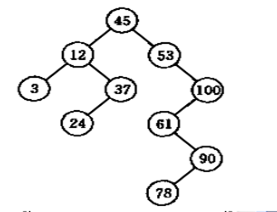
图1中,二叉树的结点值中序遍历的结果为:3,12,24,37,45,53,61,78,90,100。
结论:若按中序遍历一棵二叉排序树,所得到的结点序列是一个递增序列。
- 1. 二叉排序树(BST树)的查找思想
BST树的查找思想:
(1)首先将给定的K值与二叉排序树的根节点的关键字进行比较:若相等,则查找成功;
(2)若给定的K值小于BST树的根节点的关键字:继续在该节点的左子树上进行查找;
(3)若给定的K值大于BST树的根节点的关键字:继续在该节点的右子树上进行查找。
- 2. 二叉排序树总结
(1)查找过程与顺序结构有序表中的折半查找相似,查找效率高;
(2)中序遍历此二叉树,将会得到一个关键字的有序序列(即实现了排序运算);
(3)如果查找不成功,能够方便地将被查元素插入到二叉树的叶子结点上,而且插入或删除时只需修改指针而不需移动元素。
三、红黑树
- 1. 红黑树的定义
红黑树(Red Black Tree) 是一种自平衡二叉查找树,是在计算机科学中用到的一种数据结构,典型的用途是实现关联数组。它是在1972年由Rudolf Bayer发明的,当时被称为平衡二叉B树(symmetric binary B-trees)。后来,在1978年被 Leo J. Guibas 和 Robert Sedgewick 修改为如今的“红黑树”。红黑树和二叉平衡树(AVL树)类似,都是在进行插入和删除操作时通过特定操作保持二叉查找树的平衡,从而获得较高的查找性能。它虽然是复杂的,但它的最坏情况运行时间也是非常良好的,并且在实践中是高效的: 它可以在O(log n)时间内做查找,插入和删除,这里的n 是树中元素的数目。
- 2. 红黑树的性质
红黑树是每个节点都带有颜色属性的二叉查找树,颜色或红色或黑色。在二叉查找树强制一般要求以外,对于任何有效的红黑树我们增加了如下的额外要求:
性质1. 节点是红色或黑色。
性质2. 根节点是黑色。
性质3 每个叶节点(NIL节点,空节点)是黑色的。
性质4 每个红色节点的两个子节点都是黑色。(从每个叶子到根的所有路径上不能有两个连续的红色节点)
性质5. 从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点。
这些约束强制了红黑树的关键性质:
1.从根到叶子的最长的可能路径不多于最短的可能路径的两倍长。
结果是这个树大致上是平衡的。因为操作比如插入、删除和查找某个值的最坏情况时间都要求与树的高度成比例,这个在高度上的理论上限允许红黑树在最坏情况下都是高效的,而不同于普通的二叉查找树。要知道为什么这些特性确保了这个结果,
2.注意到性质4导致了路径不能有两个毗连的红色节点就足够了。
最短的可能路径都是黑色节点,最长的可能路径有交替的红色和黑色节点。因为根据性质5所有最长的路径都有相同数目的黑色节点,这就表明了没有路径能多于任何其他路径的两倍长。
在很多树数据结构的表示中,一个节点有可能只有一个子节点,而叶子节点不包含数据。用这种范例表示红黑树是可能的,但是这会改变一些属性并使算法复杂。为此,本文中我们使用 "nil 叶子" 或"空(null)叶子",如上图所示,它不包含数据而只充当树在此结束的指示。这些节点在绘图中经常被省略,导致了这些树好象同上述原则相矛盾,而实际上不是这样。与此有关的结论是所有节点都有两个子节点,尽管其中的一个或两个可能是空叶子。
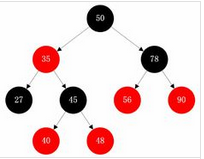
- 1. 术语
红黑树是一种特定类型的二叉树,它是在计算机科学中用来组织数据比如数字的块的一种结构。所有数据块都存储在节点中。这些节点中的某一个节点总是担当起始位置的功能,它不是任何节点的儿子,我们称之为根节点或根。它有最多两个"儿子",都是它连接到的其他节点。所有这些儿子都可以有自己的儿子,以此类推。这样根节点就有了把它连接到在树中任何其他节点的路径。如果一个节点没有儿子,我们称之为叶子节点,因为在直觉上它是在树的边缘上。子树是从特定节点可以延伸到的树的某一部分,其自身被当作一个树。在红黑树中,叶子被假定为 null 或空。由于红黑树也是二叉查找树,它们当中每一个节点的比较值都必须大于或等于在它的左子树中的所有节点,并且小于或等于在它的右子树中的所有节点。这确保红黑树运作时能够快速的在树中查找给定的值。
- 2. 用途
红黑树和AVL树一样都对插入时间、删除时间和查找时间提供了最好可能的最坏情况担保。这不只是使它们在时间敏感的应用如即时应用(real time application)中有价值,而且使它们有在提供最坏情况担保的其他数据结构中作为建造板块的价值;例如,在计算几何中使用的很多数据结构都可以基于红黑树。
红黑树在函数式编程中也特别有用,在这里它们是最常用的持久数据结构之一,它们用来构造关联数组和集合,在突变之后它们能保持为以前的版本。除了O(log n)的时间之外,红黑树的持久版本对每次插入或删除需要O(log n)的空间。
红黑树的实现:https://www.cnblogs.com/skywang12345/p/3624177.html
、哈希表的概念
在面前讨论的各种结构(线性表、树)中,记录在结构中的相对位置是随机的,和记录的关键字之间不存在确定的关系,因此,在结构中查找记录时需进行一系列和关键字的比较。这一类查找方法建立在“比较”额基础上。在顺序查找时,比较的结果为“=”与“≠”两种可能;在折半查找、二叉排序树查找,比较的结果为“<”、“=”和“>”三种可能。查找的效率依赖于查找过程中所进行的比较次数。
理想的情况是希望不经过任何比较,一次存取便能得到所查记录,那就必须在记录的储存位置和它的关键字之间建立一个确定的对应关系f,使每个关键字和结构中一个唯一的储存位置相对应。因而在查找时,只要根据这个对应关系f找到给定值k得像f(k)。若结构中存在关键字和k相等的记录,则必定在f(k)的储存位置上,由此,不需要进行比较便可直接取得所查记录。在此,我们称这个对应关系f为哈希(Hash)函数,按这个思想思想建立的表为哈希表。
我们可以举一个哈希表的最简单的例子。假设要建立一张全国30个地区的各民族人口统计表,每个地区为一个记录,记录的各数据项为:
|
编号 |
地区名 |
总人口 |
汉族 |
回族 |
··· |
显然,可以用一个一维数组c(1:30)来存放这张表其中C[i]是编号i的地区的人口情况。编号i便于记录的关键字,由他唯一确定记录的储存位置C[i]。列如:假设北京市的各民族人口,只要取出C[1]的记录即可。假如把这个数组看成是哈希表f(key)=key。然而,很多情况下的哈希函数并不如此简单。可仍以此为例,为了查看方便应以地区名作为关键字。假设地区名以汉语拼音的方式表示,则不能简单地取哈希函数f(key)=key,而是首先要将它们转化为数字,有时还要作些简单的处理。列如我们可以有这样的哈希函数:(1)取关键字中第一个字母在字母表中的序号作为哈希函数。列如:BEIJNG的哈希函数:
(1) 取关键字中第一个字母在字母表中的序号作为哈希函数。列如:BEIJING的哈希函数值为字母“B”在字母表中的序号,等于02:;
(2)先求关键字的第一个和最后一个字母在字母表中的序号之和,然后判别这个和值,若比30(表长)大,则减去30.列如:TIANJIN的首尾两个字母“T”和“N”的序号之和为34,故取04为他它的哈希函数值;或
(3)先求每个汉字的第一个字母的ASCII码(和英文字母相同)之和的八进制形式,然后将这个八进制数看成是十进制再除以30取余数,若余数为零再加上30而为哈希函数值。
例如:HENAN的两个拼音字母为“H”和“N”,他们的ASCII码之和为(266),以(266)除以(30)的余数为16,则16为HENAN的哈希函数值。上述人口统计部分关键字在这三种不同的哈希函数情况下的哈希函数值如表下图所列:
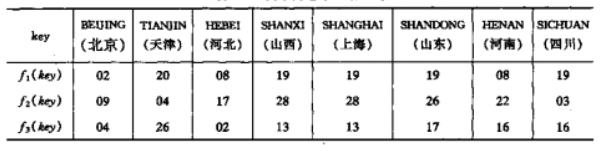
从这个例子可见:
(1) 哈希函数一个映像,因此哈希函数的设定很灵活,只要是的任何关键字由此所得的哈希函数值都落在表长允许范围之类即可;
对不同的关键字可能得到同一哈希地址,即key≠key2面f(key1)=f(key2)这种现象称冲突(collision)。具有相同函数值的关键词对该哈希函数来说乘坐同义词(synonym)。例如:关键词HEBEI和HENAN不等,但f1(HEBEI)=f1(HENAN),又如:f2(SHANGHAI):f3(HENAN)==f3(SICHUAN).这种现象给建造成困难,如在第一种哈希函数的情况下,因为山西,上海,山东和四川这四个记录的哈希地址均为19而C[19]只能存放一个记录,那么其他三个记录存放在表中的什么位置呢?并且,从上表三个不同的哈希函数的情况下就可以看出,哈希函数选的合适可以减少这种突发情况。特别是在这个例子中。只可能有30个记录,可以仔细分析这30个关键词的特性,选择一个恰当的哈希函数来避免冲突的发生。
一、 哈希函数的构造方法
构造哈希函数的方法撒很多。在介绍各种方法之前,首先需要明确什么是“好”的哈希函数。
若对于关键字集合中的任何一个关键字,经哈希函数映像到地址集合中任何一个地址的概率是相等的。则称此类哈希函数为均匀的(Uniform)哈希函数。换句话说,就是是关键字经过哈希函数得到一个“随机的地址”,以便使一组关键字的哈希地址均匀分布在整个地址区间中,从而减少冲突。
常用的构造哈希函数的方法有:
- 1. 直接定址法
取关键字或关键字的某个线性函数值为哈希地址。即:
H(Key)=key或(key)=a*key+b
其中a和b为常数(这种哈希函数叫做自身函数)。
例如:有一个从1岁到100岁的人口数字统计表,其中,年龄作为关键字,哈希函数取关键字自身。如表9.2所示
|
地址 |
01 |
02 |
03 |
.。。。 |
25 |
26 |
27 |
。。。 |
100 |
|
年龄 |
1 |
2 |
3 |
。。。 |
25 |
26 |
27 |
。。。 |
.。。。 |
|
人数 |
3000 |
2000 |
5000 |
。。。 |
1050 |
。。。 |
.。。。 |
。。。 |
。。。 |
|
。。。 |
|
|
|
|
|
|
|
|
|
表1直接定址哈希函数例之一
这样,若要询问25岁的人有多少,则只要查询的第25项即可。又如:有一个解放后出生的人口调查表,关键字是年份,哈希函数取关键字加一常数:
H(key)=key+(-1948),如表9.3所示。
|
地址 |
01 02 03 …. 22 … |
|
年份 |
1949 1950 1951 …. 1970 ….. |
|
人数 |
…. ….. ….. …. 15000 …. |
|
…. |
|
表2直接定址哈希函数例之二
这样,若要查1970年出生的人数,则只要查第)(1970-1948)=22项即可。由于直接定址所得地址集合关键词集合的大小相同。因此,对于不同的关键词不会发生冲突。但实际中能用这种哈希函数的情况很少。
- 2. 数字分析法
假设关键字是以r为基的数(如:以10为基的十进制数)。,并且哈希表中可能出现的关键字都是事先知道的,则可取关键字的若干数位组成哈希地址。例如有80个记录,其关键字为8位十进制数。假设 哈希的表长为10010,则可无取两位十进制数组成哈希地址。取哪两位?原则是使得到的哈希地址尽量避免产生冲突,则需从分析这80个关键字着手。假设这80个关键字中的一部分如下所列:

对关键字全体的分析中我们发现第1,2 位都是“8,,1”,第三位3或4, 第8位只可能取2,5,7,因此这四位数都不可取。由于中间的四位数可看成是近乎随机的,因此可取其中任意两位,获取其中两位与另外两位的叠加求和后舍去进位作为哈希地址。
- 1. 平方取中法:
取关键字平方后的中间几位为哈希地址。这是一种较常见的构造哈希函数的方法。
通常在选定哈希函数时不一定能知道关键最的全部情况,去其中哪几位也不一定合适,而一个数平方后的中间几位数的每一位都想关,由此使随机分布的关键字得到的哈希地址也是随机的。取的位数由表长决定。
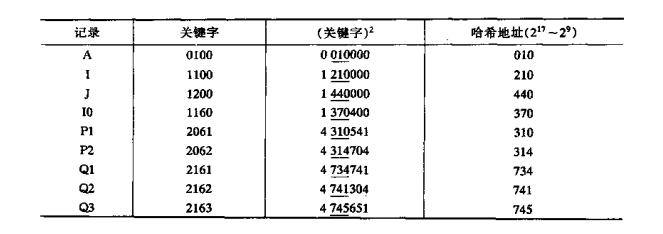
例如:为BASIC源程序中的标识符建立一个哈希表。假设BASIC语言中允许的标识符为一个字母,或一个子母和一个数字,在计算机内可用两位八位进制 数表示字母和数字。取标识符在计算机中的八进制数为它的关键字。假设表长为512=29.则可取关键字平方后的中间9二进制数为哈希地址。例如下图列出了一些标识符及它们的哈希地址。
A B C ... Z 0 1 2 ... 9
01 02 03 32 60 61 62 71
- 1. 除留余数法
取关键字被某个不大于哈希表表长m的数p除后所得余数为哈希地址。即
H(key)=key MOD p p< m(一般取小于m的最大质数
这是一种最简单,也最常用的构造哈希函数的方法。他不仅可以对关键字直接取摸(MOD),也可以在折迭、平方取中等运算之后取摸。值得注意的是,在使用除留余数法时,对p的选择很重要。若p选的不好,容易产生同义词。
一、 处理冲突的方法
在“第一小节什么是哈希表”中曾提及均匀的哈希函数可以减少冲突,但不能避免,因此,如何处理冲突是哈希表不可缺少的另一方面。
假设哈希表的地址集为0~(n-1),冲突是指由关键字得到的哈希地址为j(0≤j≤n-1)的位置上已存有记录,则“处理冲突”就是为该关键字的记录找到另一个“空”的哈希地址。
在处理冲突的过程中可能得到一个地址序列Hi i=1,2,…,k,(Hi∈[0,n-1]。
即在处理哈希地地址的冲突时,
若得到的另一个哈希地址Hi仍然发生冲突,则再求下一个地址H2 若H2仍然冲突,再求得H3. 以此类推, 直至Ha不发生冲突为止,则Ha为记录在表中的地址。
通常用的处理冲突的方法有下列几种:
- 1. 开放定址法
Hi=(H(key)+di)MODm i=1,2,…, k(k≤M-1)其中:h(key)为哈希函数;m为哈希表表长;di为增量序列,可有下列三种取法:
di=1,2,3,…,m-1,呈线性探测在散列;
例如, 在长度为11的哈希表中一填中有关键字分别为17,60,29的记录(哈希函数H(key)=key MOD11),现有第四个记录,其关键字为38 由哈希函数得到哈希地址为5,产生冲突。若用线性探测在散列的方法处理时
,得到下一个地址6,扔冲突:再求下一个地址7仍冲突
;直到哈希地址为8的位置为“空”时止处理冲突的过程结束,
记录填入哈希表中序列为8的位置。若用二次探测在散列,则应该填入序号为4的位置类似地可得到伪散列,则应该填入序号为4的位置。类似地可得到伪序列再散列的位置。
- 2. 再哈希法
i=1,2,...,k
RHi均是不同的哈希函数,即在同义词产生地址冲突时计算另一个哈希函数的地址,直到冲突不再发生。这种方法不易产生“聚集”,但增加了计算的时间。
二、 哈希表的查找及分析
在哈希表上进行查找的过程跟哈希造表过程基本一致,给定K值,根据造表时设计的哈希函数计算出哈希地址,若此位置上没有记录,则查找不成功;否则比较关键字若与给定的关键字相同,则查找成功。否则根据造表时处理冲突的方法找“下一地址”,直至哈希表中某个位置为空,或者表中所填记录的关键字与给定的关键字相等为止。
已知如图所示一组关键字按哈希函数H(key)=key MOD 13和线性探测处理冲突,构造所得的哈希表。

例如查找关键字84,H(84)=6,去6查看发现该单元格不空,但是不等于84,采用线性探测处理冲突则去下一位位置7查找,发现不空也不等于84,则再线性探测去8单元格找,不空恰好等于84,则查找成功,查找次数为3。
其他元素依次类推,可得到平均的查找长度(ASL):
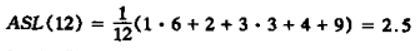
综上所述,一般情况,查找的平均长度与三个因素相关:
1、哈希函数
2、处理冲突的方法
3、装填因子
哈希表的装填因子定义为:

的值越小,发生冲突的概率越小,反正 越大,表中填入的记录越多,在填入的时候发生冲突的可能性就越大,在进行查找时候,查找的次数也就越多。
代码哈希表的实现
#include <stdio.h> #include <memory.h> #include <string.h> #include <stdlib.h> #define HARSH_TABLE_MAX_SIZE (1000) // 哈希数组的最大元素个数 typedef struct HarshNode_struct HarshNode; // 定义一个哈希表的节点 struct HarshNode_struct { char * sKey; // [sKey,nvalue]是一对键值对 int nValue; HarshNode *pNext; }; HarshNode * harshTable[HARSH_TABLE_MAX_SIZE]; // 哈希表数组 unsigned int g_harsh_table_size = 0x0; //初始化哈希表 void harsh_table_init(void) { int i = 0x0; memset(harshTable,0,sizeof(HarshNode *)*HARSH_TABLE_MAX_SIZE); g_harsh_table_size = 0x0; } // 将字符给变成hashcode unsigned int harsh_table_harsh_string(const char * sKey) { const unsigned char* p = (const unsigned char*) sKey; unsigned int value = *p; if(value) { for( p += 1; *p != '�'; p++) { value = (value << 5) - value + *p; } } return value; } //根据键值对向哈希表中添加节点,如果skey已经存在则直接更新键值nValue //添加成功返回0,添加失败返回-1 int harsh_table_insert_node(const char * sKey, int nValue) { HarshNode * pHarshNodeHead = NULL; HarshNode * pNewNode = NULL; unsigned int pos = 0x0; if((g_harsh_table_size >= HARSH_TABLE_MAX_SIZE )||(NULL == sKey)) return -1; pos = harsh_table_harsh_string(sKey) % HARSH_TABLE_MAX_SIZE; //用这种方法计算sKey在哈希数组中对应的位置 printf("skey在哈希表中的位置 : pos = %d ",pos); pHarshNodeHead = harshTable[pos]; if(NULL == pHarshNodeHead) printf("最后空指向头指针:NULL == pHarshNodeHead "); while(NULL != pHarshNodeHead ) // 如果这个位置对应的不是这一串中最后一个节点的话,那就要向后移动了 { if(strcmp(pHarshNodeHead->sKey,sKey) == 0) //如果这个键值对已经存在,只更新键值即可 { pHarshNodeHead ->nValue = nValue; return 0; } pHarshNodeHead = pHarshNodeHead->pNext; //向后移动,肯定会有NULL的时候 } pNewNode = (HarshNode *)malloc(sizeof(HarshNode)); //申请一块HarshNode 大小的内存 if(NULL == pNewNode) { return -1; } memset(pNewNode,0,sizeof(HarshNode)); pNewNode ->sKey = (char *)malloc(strlen(sKey) + 1); //申请一块sKey大小的内存 if(NULL == pNewNode ->sKey ) { return -1; } memset(pNewNode ->sKey,0,strlen(sKey) + 1); strcpy(pNewNode ->sKey,sKey); //将sKey的内容赋给 pNewNode -> sKey pNewNode ->nValue = nValue; //键值也复制过来 pNewNode ->pNext = NULL; //由于是新节点,也是尾节点,所以pNext指向NULL pHarshNodeHead = pNewNode; harshTable[pos] = pHarshNodeHead; //最后一定要让数组中的这个位置指向这个头指针 g_harsh_table_size ++; return 0; } //打印数组中对应的某个位置的那一串哈希值 void print_harsh_node(int pos) { HarshNode * pHarshNodeHead = NULL; if(pos >= HARSH_TABLE_MAX_SIZE) return; pHarshNodeHead = harshTable[pos]; if(NULL == pHarshNodeHead) printf("NULL == pHarshNodeHead "); while(NULL != pHarshNodeHead) { printf("位置:%d, sKey:%s, nValue:%d ",pos,pHarshNodeHead->sKey,pHarshNodeHead->nValue); pHarshNodeHead = pHarshNodeHead->pNext; } } // 根据键值sKey来查找对应的哈希节点 HarshNode * harsh_table_lookup(const char *sKey) { unsigned int pos = 0x0; HarshNode * pHarshHead = NULL; if(NULL == sKey) { return NULL; } pos = harsh_table_harsh_string(sKey) % HARSH_TABLE_MAX_SIZE; //计算出在哈希数组中的位置 pHarshHead = harshTable[pos]; while(NULL != pHarshHead) { if(strcmp(sKey,pHarshHead->sKey) == 0)//找到了 return pHarshHead; pHarshHead = pHarshHead->pNext; // 没有找到的话来到下一个节点 } return NULL; } void main(void) { char * pSkey = "abcd"; int nValue = 1234; int ret = -1; int pos = 0xffffffff; HarshNode * pHarshNode = NULL; harsh_table_init(); ret = harsh_table_insert_node(pSkey,nValue); printf("ret = %d ",ret); if(!ret) { pos = harsh_table_harsh_string(pSkey) % HARSH_TABLE_MAX_SIZE; printf("main: pos = %d ",pos); print_harsh_node(pos); } pHarshNode = harsh_table_lookup(pSkey); if(NULL != pHarshNode) { printf("最终值: sKey:%s, nValue: %d ",pHarshNode->sKey,pHarshNode->nValue); } }
代码求最小公倍数
/* Note:Your choice is C IDE */ #include "stdio.h" void main() { int max,k,i,s,j; printf("请输入一个数:"); scanf("%d",&k); printf("请输入第二个数:"); scanf("%d",&s); /* if(k<s) { j=k; k=s; s=j; }*/ /* k已然成了较大数 */ for(i=1;i<=s&&i<=k;i++) { if(s%i==0&&k%i==0) { max=i; } } printf("最大公约数%d ",max); printf("最小公倍数%d",k*s/max); }