NOIP2018 保卫王国

NOIP2018 保卫王国

Online Judge：NOIP2018 day2 T3

Label：树形Dp，思维题，好题，倍增，LCA，DDP(动态DP)

题目描述

一棵n个节点的树，每个节点有一个权值(wi)，一共m个询问，每个询问由((a,x,b,y))构成，a,b为节点编号，x,y的取值为0或1，表示该节点必须覆盖(1)或必须不能覆盖(0)，对于每个询问，求此情况下该树的最小权覆盖集(每条边都必须至少有一个端点被覆盖)。询问彼此独立。

(n,m<=10^5)

Hint

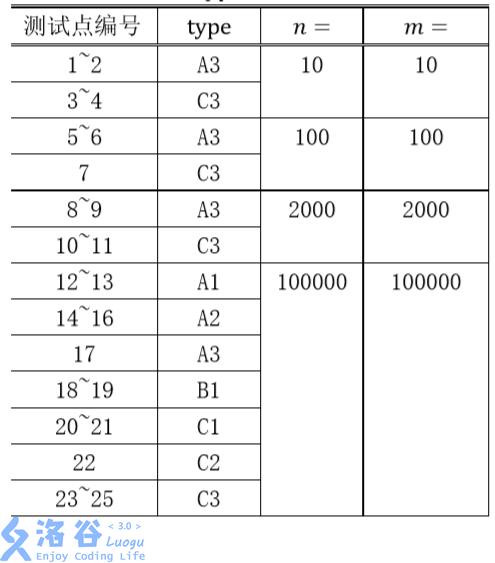
数据类型的含义：

A：城市i与城市i+1直接相连。
B：任意城市与城市 1 的距离不超过 100（距离定义为最短路径上边的数量），即如果这棵树以 1 号城市为根，深度不超过 100。
C：在树的形态上无特殊约束。
1：询问时保证a = 1,x = 1，即要求在城市 1 驻军。对b,y没有限制。
2：询问时保证a,b是相邻的（由一条道路直接连通）
3：在询问上无特殊约束。

---

这一题可以切出好多种分来，下面的部分分只切了44的暴力一档，类型1，类型2，总共84分的切分。

Subtask0

对于数据点1~11，nm范围较小，直接对于每个询问都做一遍树形DP。复杂度为(O(nm))。

(f[x][0/1])表示x选/不选时，以x为根的子树的最小花费。每次询问时根据操作对对应的f值赋上正无穷，表示不可转移这一种状态。

Subtask1

对于类型1，保证a=1,x=1，即要求在城市1驻军，对b,y没有限制。

也就是现在每个询问只会修改一个节点的状态(节点1的状态在一开始就可以直接修改，而不用每个询问都改一遍)。由于只讨论一个节点的状态，直接up and down​合并即可，也就是预处理出两个数组，一个表示x子树外的情况(不包含x)，一个表示x子树内的情况。

其中第二个数组就是上面的(f[x][0/1])，表示x选/不选时，以x为根的子树的最小花费；第一个数组设为(g[x][0/1])，表示x选/不选时，x子树外的花费。（相当于把整棵树倒过来，以x为根，但剖去原来以x为根的子树，类似换根）。

每次询问时直接合并这两个数组

while(m--){
	int x=read(),op1=read(),y=read(),op2=read();		
	int ans=dp[y][op2]+dp2[y][op2];			
	if(ans>=INF)puts("-1");
	else printf("%lld
",ans);
}

复杂度为(O(n+m))。对应数据点为12,13,18,19,20,21。结合Substack0期望得分68。

Subtask2

对于类型2，询问时保证a,b是相邻的（由一条道路直接连通）。虽然有两个节点的状态需要固定，但由于这两点间没有节点，仍然可以用上面的up&down去做。

每次回答询问时需要特别讨论一下，令y作为x的儿子，则还应算上x子树中除了y子树的部分。

while(m--){
	int x=read(),op1=read(),y=read(),op2=read();			if(dep[x]>dep[y])swap(x,y),swap(op1,op2);
	if(op1==0&&op2==0){puts("-1");continue;}
	int other;
	if(op1==1)other=dp[x][1]-min(dp[y][0],dp[y][1]);
	else other=dp[x][0]-dp[y][1];	
	printf("%lld
",other+dp2[x][op1]+dp[y][op2]);
}

复杂度同样为(O(n+m))。对应数据点为14,15,16,22。结合前两个算法期望得分84。

前84分的切分代码.

AC做法

DDP做法太巨了没敢看qwq...

下面是一种基于上面upanddown改进的倍增跳LCA做法。

参考了这篇博客的代码->

每次固定x,y的状态时，只会影响到路径((x-y))、路径((lca->root))上节点的DP值，其中lca是x,y的最近公共祖先，root即树根(也就是节点1)。发现影响到的节点好像不太多，而且都是往上向祖先的，如果每次都重新更新整个树太浪费时间了。

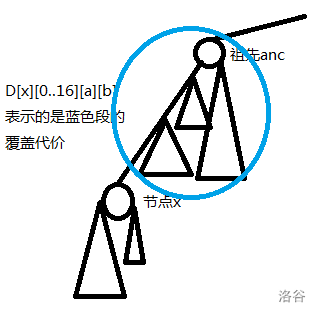
注意到，既然影响到的都是祖先，想到记录自己到某个祖先的状态，由于内存问题，改成倍增记录。(D[x][i=0..16][a=0/1][b=0/1])，表示从x到其向上第(2^i)个祖先anc的花费，并且此时x的状态为a，anc的状态为b。

关于从x到祖先anc的花费这个有点抽象，看图理解

预处理w数组的部分如下。

for(int i=1;i<=n;++i){
	int x=Fa[i][0];
	D[i][0][0][0]=INF;
	D[i][0][0][1]=f[x][1]-min(f[i][0],f[i][1]);
	D[i][0][1][0]=f[x][0]-f[i][1];
	D[i][0][1][1]=D[i][0][0][1];
}
for(int j=1;j<=16;++j){
	for(int i=1;i<=n;++i){
		int x=Fa[i][j-1];
		if(!Fa[x][j-1])continue;
		Fa[i][j]=Fa[x][j-1]; 
		for(int a=0;a<=1;++a)for(int b=0;b<=1;++b){
			D[i][j][a][b]=INF;
			for(int o=0;o<=1;++o){
				D[i][j][a][b]=min(D[i][j][a][b],D[i][j-1][a][o]+D[x][j-1][o][b]);
			}
		}
	}
}

接下来问题是如何往上跳。

直接上代码理解，整个函数的框架就是倍增求lca的框架。先将xy跳至同一深度，然后再将xy跳至lca的儿子处，最后再统计(lca-根)路径上的，以及lca中除去(xy分别占据子树)的剩余部分。也就是下图的部分

int solve(int op1,int x,int op2,int y){
	if(dep[x]<dep[y])swap(x,y),swap(op1,op2);
	int nowx[2],lstx[2],nowy[2],lsty[2];
	//now,lst用于滚动记录 
	lstx[0]=lstx[1]=lsty[0]=lsty[1]=INF;
	lstx[op1]=f[x][op1];
	lsty[op2]=f[y][op2];
	int step=dep[x]-dep[y];
	for(int i=16;i>=0;i--){
		if(step&(1<<i)){
			nowx[0]=nowx[1]=INF;
			for(int a=0;a<=1;++a)for(int b=0;b<=1;++b){//a祖先状态，b跳上来的子孙状态
				nowx[a]=min(nowx[a],lstx[b]+D[x][i][b][a]); 
			} 
			
			lstx[0]=nowx[0];
			lstx[1]=nowx[1];
			x=Fa[x][i];
		}
	}
	if(x==y)return lstx[op2]+g[y][op2];
    for(int i=16;i>=0;i--){
        if(Fa[x][i]!=Fa[y][i]){
            nowx[0]=nowx[1]=nowy[0]=nowy[1]=INF;
            for(int a=0;a<=1;a++)for(int b=0;b<=1;b++){
                nowx[a]=min(nowx[a],lstx[b]+D[x][i][b][a]);
                nowy[a]=min(nowy[a],lsty[b]+D[y][i][b][a]);
            }
            lstx[0]=nowx[0];lstx[1]=nowx[1];
			x=Fa[x][i];
            lsty[0]=nowy[0];lsty[1]=nowy[1];
			y=Fa[y][i];
        }
	}
    int lca=Fa[x][0];
    //当lca不选时 
    int ans1=f[lca][0]+g[lca][0]-f[x][1]-f[y][1]+lstx[1]+lsty[1];
    //当lca选时
	int ans2=f[lca][1]+g[lca][1]-min(f[x][0],f[x][1])-min(f[y][0],f[y][1])
    		+min(lstx[0],lstx[1])+min(lsty[0],lsty[1]);
    return min(ans1,ans2);
}

完整代码。