求解逆元有如下几种方式：
1. 如果 mod 为 素数，那么可以使用费马小定理+快速幂求解
2. 如果 gcd(a,mod)==1 其中，a为求逆元素，并且满足前面的等式保证a存在逆元。 那么可以使用 扩展欧几里得
3. 递推法快速打表求解多个逆元， 要求 mod 必须为奇质数
4. 如果 mod 不为素数，那么可以使用通用解法，这里不详细讲（因为我也不会
下面讲解1，2，3方法
方法一：（如果 mod 为 素数，那么可以使用费马小定理+快速幂求解）
1. 费马小定理
如果 gcd(a,p) == 1， 并且 p 为素数，那么就有 
公式变形：
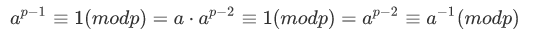
所以：求解 a 的逆元，就是求解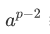 
。因此需要使用到快速幂
2. 代码：求 a 在 mod 下的乘法逆元
1 //求 m^n % k 2 ll quick_power(ll m, ll n, ll k){ 3 ll ans = 1; 4 m %= k; 5 while(n){ 6 if(n & 1) 7 ans = ans * m % k; 8 n >>= 1; 9 m = m * m % k; 10 } 11 return ans; 12 } 13 14 ll inverse_quick_pow(ll a, ll mod){ 15 return quick_power(a,mod-2,mod); 16 }
方法二：如果 gcd(a,mod)==1 其中，a为求逆元素，并且满足前面的等式保证a存在逆元。 那么可以使用 扩展欧几里得
1. 扩展欧几里得：传送门
2. 由于求解逆元，其实就是解方程 ax+py ≡ 1 (mod p)
3. 代码: 求 a 在 mod 下的乘法逆元
1 //ax + by = gcd(a,b) 2 //gcd 保存了 a,b 的最大公约数 3 void ext_gcd(ll a, ll b, ll &gcd, ll &x, ll &y) { 4 if (!b) { gcd=a; x=1; y=0; } 5 else { ext_gcd(b,a%b,gcd,y,x); y-=(a/b)*x; } 6 // 理解上面这个这句话就用上面的 extend_gcd 来理解，主要是使用了引用的概念 7 // 并且 ext_gcd 在 y-=(a/b)*x 上面，也就是说 ext_gcd 参数中的 x,y 都是 8 // 下一层函数返回的 x2, y2 9 // 然后使用 y-=(a/b)*x 处理一下本层函数 y1 即可 10 } 11 12 13 ll inverse_ext_gcd(ll a, ll mod) { 14 ll x, y, gcd; 15 ext_gcd(a, mod, gcd, x, y); 16 // gcd(x,mod) ==1 是有逆元的充要条件 17 // 当满足有逆元的时候，需要调整 x 到 0-mod 之间 18 // 对于负数 x+mod 即可调整正确， 19 // 为了编码统一将正数页进行调整， (x+mod)%mod 20 return gcd == 1 ? (x + mod) % mod : -1; 21 }
方法三：递推法快速打表求解多个逆元， 要求 mod 必须为奇质数
1. 原理：基于一个公式 
2. 初始条件： inv[1]=1;
3. 代码：
1 // 递推法快速求 逆元 2 const int maxn = 3e3 + 5; 3 ll inv[maxn]; 4 5 //要求： mod 为奇质数 6 //公式: inv[i]=(mod - mod /i) * inv[mod%i]%mod 7 //初始条件: inv[1]=1; 8 void inverse_recursion(ll mod) { 9 inv[1] = 1; 10 for (int i = 2; i < maxn; i++) 11 inv[i] = (mod - mod / i) * inv[mod % i] % mod; 12 }