dijkstra算法优先队列

d[i] 是起点到 I 节点的最短距离

void Dijkstra(int s) {
    priority_queue<P, vector<P>, greater<P> > que;
    fill(d, d + MAXN, INF);
    d[s] = 0;
    que.push(make_pair(0, s));  //first:d[i] second:i 
    while (!que.empty()) {
        P p = que.top(); que.pop();
        int v = p.second;
        if(d[v] < p.first) continue;    //如下图   //d[v] < p.first 说明，v 点已经通过其他路径变得松弛，距离更短。而 p.first 只是之前入队的旧元素
        for (int i = 0; i < G[v].size(); i++) {
            edge e = edges[G[v][i]];
            if (d[e.to] > d[v] + e.cost) {
                d[e.to] = d[v] + e.cost;
                que.push(P(d[e.to], e.to));
            }
        }
    }
}

---

if(d[v] < p.first) continue;

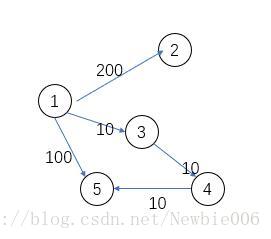
解释：以 1 为起点，第一次遍历会将2，3，5(I) 全部加入队列。然后出队3，然后4，然后更新5， 5(II)又入队，5(II)没有出度，然后5(II)出队，接着第一轮的 5(I) 出队，但是此时 5(I) 已经不是这个点已经不满足最短路径存在定理，所以不能再更新和5相关联的边，应该直接让其出队。也就是这个判断条件

如果不使用这个判断，也可以开一个 vis 数组，用来标记，只要是更新过的节点就不能再次更新周围的节点。