2020牛客寒假算法基础集训营6 H-云

题目链接：H-云

题意:

现在天空(可视为二维平面)中有 N 朵 A 类云，M 朵 B 类云，每朵云的形状都可以用边平行于坐标轴的矩形来描述。
一开始，A 类云在第三象限，B 类云在第一象限，没有任何云和坐标轴有交点。
随着风的吹拂，A 类云以每秒一个单位的速度向右移动，B 类云以每秒一个单位的速度向下移动，当一朵 A 类云和一朵 B 类云在某一个时刻有了至少一个公共点，它们就相遇了。
现在请你告诉小 R，有多少对 A 类云和 B 类云能够相遇。
1≤N,M≤100,000，1≤|Xi|,|Yi|,|Pi|,|Qi|≤109

思路：

这道题比较有意思的是相遇的判断条件进行转化，最后成为数轴上投影是否有重叠。

直观的想两朵云要相遇则 A云右侧到B云左侧-A云左侧到B云右侧 的时间段和 A云上侧到B云下侧-A云下侧到B云上侧 的时间段范围重叠。但是这样的话意味着要把所有云的时间全部两两计算一边 O(n²）显然不行

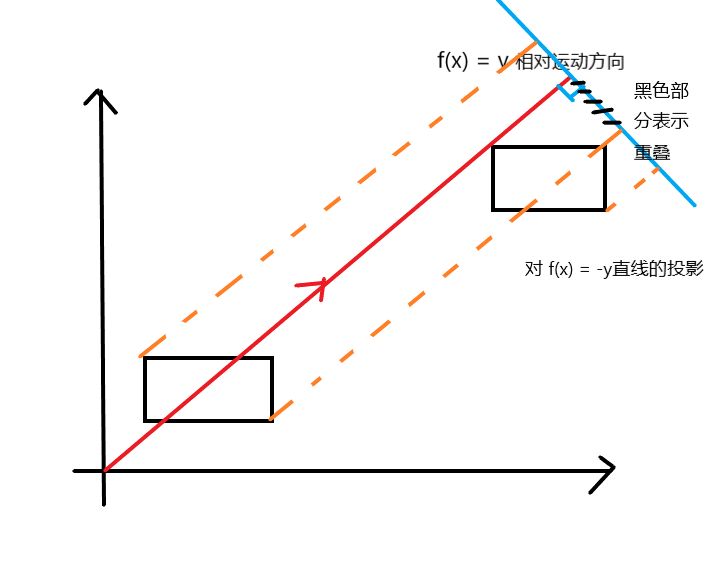
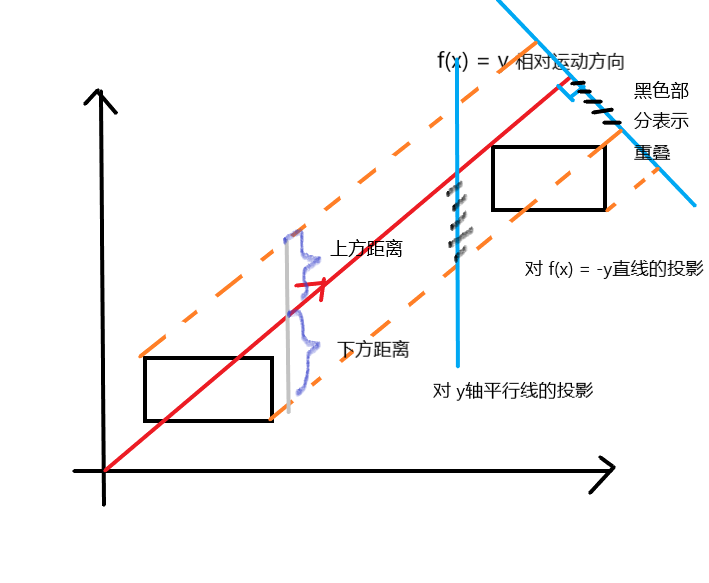
再考虑相对运动的情况，由于两朵云之间运动可以相对为一种云沿 x = y直线的方向进行运动。而相交的判断可以以左上和右下角的点沿 y = x 作平行线投影到 y = -x上面，同样我们还可以转化为投影到 y轴平行线上达到相同的效果，这样更加方便转化。仅通过 xi-yi 就可以确定在 y = x直线的上方或者下方距离

这样以来就可以判断两矩形是否会相遇了。而接下来对于计数问题 , 我们只需要对 坐标点距离排序，类似 扫描线的操作（矩形投影的左端点计数加一，到右端点计数减一），这样就完成统计了。

code:

#include<cstdio>
#include<iostream>
#include<algorithm>
#include<string>
#include<cstring>
typedef long long ll;
const int maxn = 1e6+7;
using namespace std;
struct cloud{
    int dis,lr,type;
    bool operator < (const cloud& b){
        return dis==b.dis?lr>b.lr:dis<b.dis;
    }
}cd[maxn<<1];
int main(){
    int N,M;
    scanf("%d%d",&N,&M);
    int tot = 1;
    for(int i=1;i<=N;i++){
        int x,y,p,q;
        scanf("%d%d%d%d",&x,&y,&p,&q);
        cd[tot++] = (cloud){x-y,1,0};
        cd[tot++] = (cloud){p-q,-1,0};
    }
    for(int i=1;i<=M;i++){
        int x,y,p,q;
        scanf("%d%d%d%d",&x,&y,&p,&q);
        cd[tot++] = (cloud){x-y,1,1};
        cd[tot++] = (cloud) {p-q,-1,1};
    }
    ll ans = 0;
    sort(cd+1,cd+tot+1);
    int cont[2] = {0,0};
    for(int i=1;i<tot;i++){
        cont[cd[i].type] += cd[i].lr;
        if(cd[i].lr==1) ans+=cont[cd[i].type^1];
    }
    printf("%lld
",ans);
    return 0;
}