基本的二维变换可包括旋转、缩放、扭曲,和平移四种,
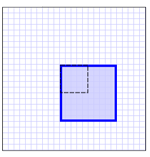

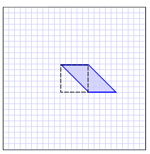
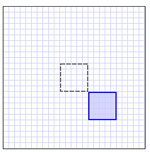
而这些几何运算则可以转换为一些基本的矩阵运算:
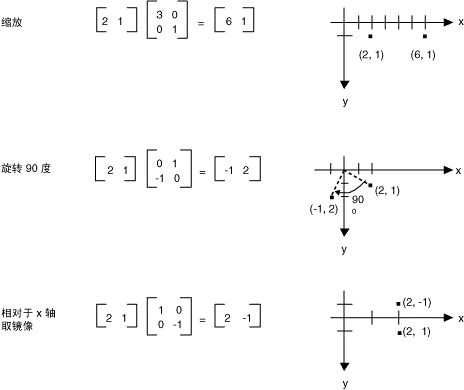
这几个变换都是线性的,但平移运算不是线性的,不能通过2*2矩阵运算完成。若要将点 (2, 1)在 x 方向将其平移 3 个单位,在 y 方向将其平移 4 个单位。 可通过先使用矩阵乘法再使用矩阵加法来完成此操作。
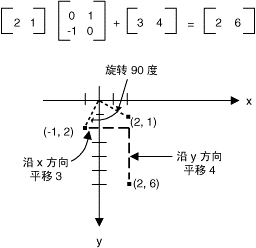
综合这几种基本运算,数学家们将其统一为一个3*3矩阵,存储形式如下:
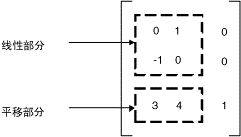
由于表示仿射变换的矩阵的第三列总是(0,0,1),在存储矩阵的时候,大多只存成一个2*3的数组。
变换的原点
二维变换的参考点是非常重要的,例如如下旋转的结果就大不相同:
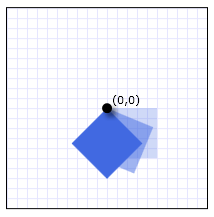
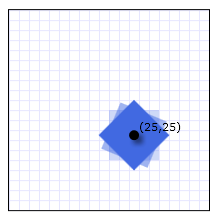
当然,有一种特殊的变换除外。那就是平移变换,无论原点是什么其变换的结果都是没有变化的。
复合变换
复合变换的矩阵可通过将几个单独的变换矩阵相乘而得到,这就意味着任何仿射变换的序列均可存储于单个的 Matrix 对象中。
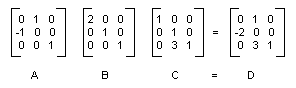
需要注意的是,复合变换是有顺序的,一般说来,先旋转、再缩放、然后平移,与先缩放、再旋转、然后平移是不同的。
逆矩阵
可以根据一定的运算求出某个矩阵的逆矩阵,这个矩阵可以用来求出新的坐标点在原坐标系的位置。但需要注意的是,并非所有矩阵都是可逆的,可逆矩阵要求是非奇异矩阵。
在线预览
微软有一个几何变换的在线预览的页面,可以非常直观的帮助我们理解这些变换,感兴趣的朋友不妨试试。
http://ie.microsoft.com/testdrive/Graphics/hands-on-css3/hands-on_2d-transforms.htm
小结
矩阵运算其实是非常基础的数学知识,在图形学中应用得还是非常广泛的,但大学学的时候往往不知道干嘛用,现在用的时候却又忘了啥原理了。本文这里只是介绍了一些矩阵运算的基本概念,具体详细的内容可以参考下下面的这些参考资料。下一篇文章再简单的介绍一下矩阵变换的实际使用。
参考资料: