关于三角形

基本性质:

1、三角形两边之和大于第三边，两边之差小于第三边。

2、三角形内角和为180度，外角和为360度。

3、三角形共三个内角，三个外角。

4、三角形的一个外角等于与它不相邻的两个内角的和。

5、三角形有三条高。

6、三角形的三条角平分线交于一点。

7、等底等高的两个三角形面积相等。

8、三角形可以分为等边三角形和不等边三角形。

9、有两条边相等的三角形叫做等腰三角形。

10、等腰三角形两个底角相等

11、有一个角是60度的等腰三角形是等边三角形。

12、等边三角形每个内角都是60度。

13、等腰三角形的高、中线、角平分线交于一点。

14、等腰三角形和等边三角形都是轴对称图形。

15、等边三角形有3条对称轴。

16、能够完全重合的两个三角形互为全等三角形。

17、有三条边相等，两边与其夹角对应相等，两角一边对应相等，直角三角形一条直角边与斜边对应相等的两个三角形全等。

18、全等三角形对应边相等，对应角相等。

19、三角形的内角最多只有一个大于90度。

20、三角形至少有两个锐角。

21、三角形的三条高交与外部，内部或某一顶点。

22、全等三角形的面积和周长也都相等。

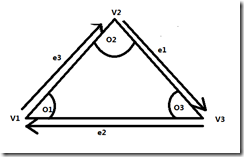
根据上图对应关系我们有

e1 = v3 – v2      L1 = || e1 ||

e2 = v1 – v3      L2 = || e2 ||

e3 = v2 – v1      L3 = || e3 ||

正弦公式:

sin(O1)/L1 = sin(O2)/L2 = sin(O3)/L3

余弦公式:

L1² = L2² + L3² – 2 * L2 * L3 * cos(O1)

L2² = L1² + L3² – 2 * L1 * L3 * cos(O2)

L3² = L1² + L2² – 2 * L1 * L2 * cos(O3)

周长:

P = L1 + L2 + L3

面积:

三角形面积是平行四边形面积的一半:

以b为底，h为高

S = (b * h)/2

海伦公式:

L = (L1 + L2 + L3)/2

S = √( L * (L – L1) * (L – L2) * (L – L3) )

2D中用定点坐标计算三角形面积:

S = ( (y1 - y3)*(x2 - x3) + (y2 - y3) * (x3 - x1) )/2

3D中用叉乘计算面积:

关于叉乘和四边形面积

S = ( || e1 * e2 ||)/2

重心坐标系:

我们经常碰到需要知道三角形上某个点的坐标，比如射线和三角形的焦点

那么我们就需要一个能与三角形表面相关联并且独立于三角形所在3D坐标空间，这样重心坐标空间就诞生了.

      三角形所在平面任一点都能表示为顶点的加权平均值。这个权就称作重心坐标.

从重新坐标(b1,b2,b3)到标准3D的转换为:

p = b1 * V1 + b2 * V2 + b3 * v3

      重心坐标的中和为1 即：

b1 + b2 + b3 = 1

    比如 三角形顶点v1的重心坐标就是(1,0,0),3D坐标就可以表示为:

p = b1 * v1 + b2 * v2 + b3 * v3

p = 1 * v1 + 0 * v2 + 0 * v3

p = v1

其他两个顶点同理。

    由此可以看出，三角形三个顶点重心坐标都是单位向量，即:

v1 = (1,0,0)

v2 = (0,1,0)

v3 = (0,0,1)

注意：

       不只是三角形内的点，该平面上的所有点都能用重心坐标描述。三角形内的点重心坐标在0到1之间的变化,

三角形外的点至少有一个坐标为负。重心坐标用和原三角形大小相同的块“镶满”整个平面.

2D中计算点的中心坐标:

根据公式P = b1*V1 + b2*V2 + b3*v3 得:

Px = b1 * x1 + b2 * x2 + b3 * x3

py = b1 * y1 + b2 * y2 + b3 * y3

1   = b1         + b2          + b3

解方程组:

b1 = [ (Py - y3) * (x2 - x3) + (y2 - y3) * (x3 – Px) ] / [ (y1 - y3) * (x2 - x3) + (y2 - y3) * (x3 -x1) ]

b2 = [ (Py - y1) * (x3 - x1) + (y3 - y1) * (x1 – Px) ] / [ (y1 - y3) * (x2 - x3) + (y2 - y3) * (x3 -x1) ]

b3 = [ (Py - y2) * (x1 - x2) + (y1 - y2) * (x2 – Px) ] / [ (y1 - y3) * (x2 - x3) + (y2 - y3) * (x3 -x1) ]

可以看出分母是三角形面积的2倍，并且各式的分子都是重心坐标所对应的“子三角形”面积的2倍，把上面公式解释成面积比,得:

2 * S(T)   = (y1 - y3) * (x2 - x3) + (y2 - y3) * (x3 -x1)

2 * S(T1) = (Py - y3) * (x2 - x3) + (y2 - y3) * (x3 – Px)

2 * S(T2) = (Py - y1) * (x3 - x1) + (y3 - y1) * (x1 – Px)

2 * S(T3) = (Py - y2) * (x1 - x2) + (y1 - y2) * (x2 – Px)

所以:

b1 = 2 * S(T1) /( 2 * S(T) )  =  S(T1)  / S(T)

b2 = 2 * S(T2) /( 2 * S(T) )  =  S(T2)  / S(T) 

b3 = 2 * S(T3) /( 2 * S(T) )  =  S(T3)  / S(T)

提示:

    S(T1)指的是与顶点v1相对的哪个子三角形，也就是和v1相对的那条边(v3 - v2)所组成的三角形  P  –   v2  – v3;

    S(T2)指的是与顶点v2相对的哪个子三角形，也就是和v2相对的那条边(v1 - v3)所组成的三角形 v1 –   P   – v3;

    S(T3)指的是与顶点v3相对的哪个子三角形，也就是和v3相对的那条边(v2 - v1)所组成的三角形 v1 –   v2  – p.

还可以应用克莱姆法则:

根据方程组 得:

	x1   x2  x3		Px   x2   x3		x1   Px  x3		x1   x2   Px
D=	y1   y2  y3	D1=	Py   y2   y3	D2 =	y1   Py  y3	D3 =	y1   y2   Py
	1     1    1		1     1     1		1     1    1		1     1     1

b1 = D1 / D

b2 = D2 / D

b3 = D3 / D

3D中计算点的重心坐标:

计算3D中任意点的重心坐标比在2D中复杂，不能再像以前那样解一个方程组了，因为有三个未知数和四个方程。另一个导致复杂性的地方是p可能不在三角形所在的平面中，这时重心坐标没有意义，但现在我们假设p在三角形所在的平面上。

一种技巧是通过抛弃x、y、z中的一个分量，将3D问题转化到2D中，这和将三角形投影到三个基本平面中某一个上的原理相同。理论上，这是能解决问题的，因为投影面积和原面积成比例。

那么应该抛弃哪个坐标呢？不能总是抛弃某一个，因为如果三角形垂直于某个平面，投影点将共线。如果三角形接近垂直于投影平面，会遇到浮点数精度问题。一种解决方法是挑选投影平面，使得投影面积最大。这可以通过检查平面的法向量做到，我们要抛弃的就是绝对值最大的坐标。例如，法向量为[-1, 0, 0]，我们将抛弃顶点p的x分量，把三角形投影到yz平面。下面的代码展示了怎样计算3D中任意点的重心坐标：

Listing 12.3: Computing barycentric coordinates in 3D
bool computeBarycentricCoords3d(
const Vector3 v[3], // vertices of the triangle
const Vector3 &p, // point that we wish to compute coords for
float b[3] // barycentric coords returned here
)
{
// First, compute two clockwise edge vectors
Vector3 d1 = v[1] – v[0];
Vector3 d2 = v[2] – v[1];
// Compute surface normal using cross product. In many cases
// this step could be skipped, since we would have the surface
// normal precomputed. We do not need to normalize it, although
// if a precomputed normal was normalized, it would be OK.
Vector3 n = crossProduct(d1, d2);
// Locate dominant axis of normal, and select plane of projection
float u1, u2, u3, u4;
float v1, v2, v3, v4;
if ((fabs(n.x) >= fabs(n.y)) && (fabs(n.x) >= fabs(n.z)))
{
// Discard x, project onto yz plane
u1 = v[0].y – v[2].y;
u2 = v[1].y – v[2].y;
u3 = p.y – v[0].y;
u4 = p.y – v[2].y;
v1 = v[0].z – v[2].z;
v2 = v[1].z – v[2].z;
v3 = p.z – v[0].z;
v4 = p.z – v[2].z;
}
else if (fabs(n.y) >= fabs(n.z))
{
// Discard y, project onto xz plane
u1 = v[0].z – v[2].z;
u2 = v[1].z – v[2].z;
u3 = p.z – v[0].z;
u4 = p.z – v[2].z;
v1 = v[0].x – v[2].x;
v2 = v[1].x – v[2].x;
v3 = p.x – v[0].x;
v4 = p.x – v[2].x;
}
else
{
u1 = v[0].x – v[2].x;
u2 = v[1].x – v[2].x;
u3 = p.x – v[0].x;
u4 = p.x – v[2].x;
v1 = v[0].y – v[2].y;
v2 = v[1].y – v[2].y;
v3 = p.y – v[0].y;
v4 = p.y – v[2].y;
}
// Compute denominator, check for invalid
float denom = v1 * u2 – v2 * u1;
if (denom == 0.0f)
{
// Bogus triangle - probably triangle has zero area
return false;
}
// Compute barycentric coordinates
float oneOverDenom = 1.0f / denom;
b[0] = (v4*u2 – v2*u4) * oneOverDenom;
b[1] = (v1*u3 – v3*u1) * oneOverDenom;
b[2] = 1.0f – b[0] – b[1];
// OK
return true;
}

另一种计算3D重心坐标的方法基于用向量叉乘计算3D三角形面积的方法。给出三角形的两个边向量e₁和e₂，三角形面积为||e₁x e₂|| / 2。一旦有了整个三角形的面积和三个"子三角形"的面积，就能计算重心坐标了。

还有一个小小的问题：叉乘的大小对顶点的顺序不敏感。根据定义，叉乘大小总是正的。这种方法不适用于三角形外的点，因为它们至少有一个负的重心坐标。

看看能否找到解决问题的思路。当顶点以"不正确"的顺序列出时，向量叉乘的大小可能会是负值，我们需要一种正确计算的方法。幸运的是，有一种非常简单的方法能做到这一点：点乘。

设c为三角形两个边向量的叉乘，c的大小等于三角形面积的两倍。设有一个单位法向量n，n和c是平行的，因为它们都垂直于三角形所在的平面。当然，它们的方向可能是相反的。两向量的点乘等于它们大小的积再乘以它们夹角的cos值。因为n是单位向量，不管n和c方向相同还是相反，都有：

c . n = ||c|| ||n|| cosθ = ||c|| (1) (±1) = ±||c||

将这个面积除以2，就得到了3D中三角形的"有符号"面积。有了这个技巧，就能利用前一节的结论：b_i就是"子三角形"T_i的面积占整个三角形面积的比。如图12.22所示，标出了所有用到的向量。

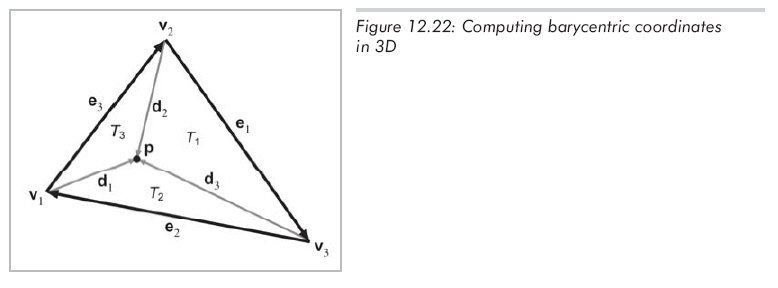
正如你所看到的，每个顶点都有一个向量d_i，它从v_i指向p，列出这些向量满足的方程：

注意到所有的分子和分母中都有n，因此，实际上并不必单位化n。此时，分母为n . n。

这种计算重心坐标的方法比向2D投影的方法用到了更多的标量数学运算。但是它没有分支，并为向量处理器提供了更多的优化机会。因此它在有向量处理器的超标量体系结构中会更快一些。

特殊点

重心是三角形的最佳平衡点，它是三角形三条中线的交点（中线指从顶点到对边中点的连线）。图12.23展示了一个三角形的重心。

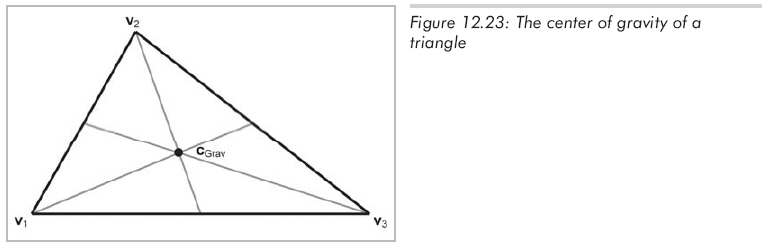
重心是三个顶点的几何均值：

c_grav = (v₁+ v_{2 +} v₃) / 3

重心坐标为：

(1/3, 1/3, 1/3)

重心也被称作质心。

内心是指到三角形各边距离相等的点。之所以称作内心是因为它是三角形内切圆的圆心，内心是角平分线的交点，如图12.24所示：

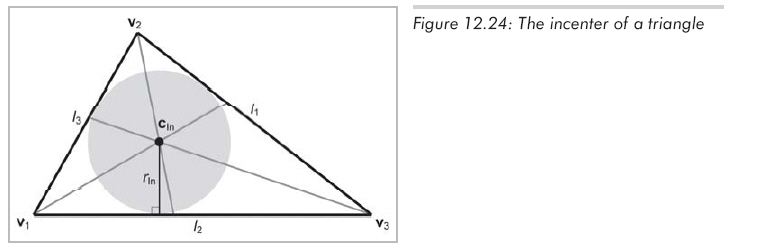
内心的计算：

c_in = (L₁v₁ + L₂v₂ + L₃v₃) / p

p = L₁ + L₂ + L₃是三角形的周长，因此，内心的重心坐标为：

（L₁/p, L₂/p,L₃/p）

内切圆的半径可由三角形面积除以周长求得：

r_in = A/p

内切圆解决了寻找与三条直线相切的圆的问题。

外心是三角形中到各顶点距离相等的点，它是三角形外接圆的圆心。外心是各边垂直平分线的交点。图12.25展示了一个三角形的外心。

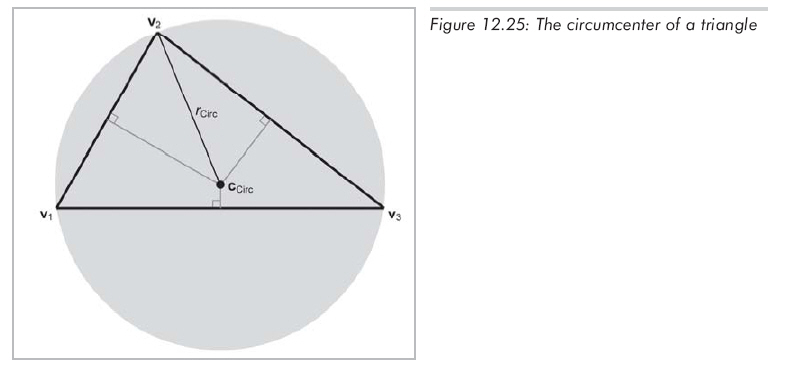
为了计算外心，先定义以下临时变量：

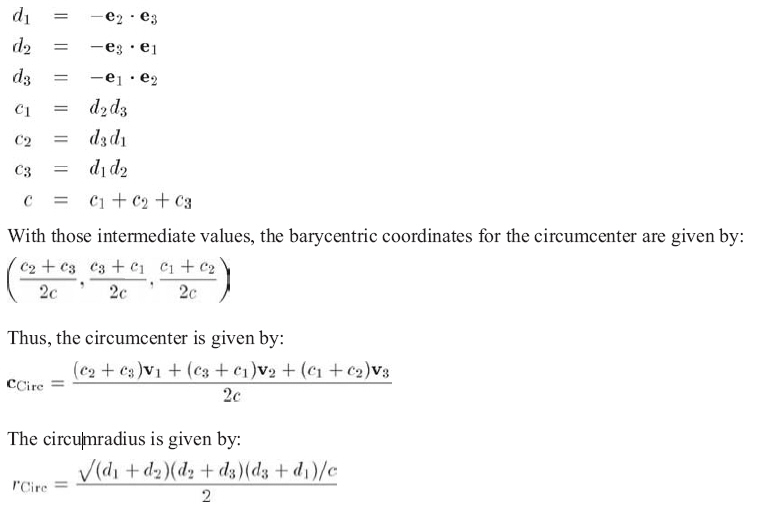
外心和外接圆半径解决了寻找过三个点的圆的问题。