在美术中，特别是绘画，人类掌握了通过在图像的内容和风格间建立复杂的相互作用从而创造独特的视觉体验的技巧。到目前为止，这个过程的算法基础是未知的，也没有现存的人工系统拥有这样的能力。然而在视觉感知的其他重要方向，如目标和人脸识别，一种受生物启发的深层神经网络最近展示了接近人类的表现。本文介绍了一种基于深层神经网络的人工神经网络系统，能够产生高感知质量的图片。该系统利用神经表示来分离和重组任意图像的内容和风格，为艺术图片创作提出了一种神经算法。不仅如此，在性能优良的人工神经网络和生物视觉的相似性之间，我们的工作提供了一条人类如何创造和感知艺术图像的算法理解之路。
深层神经网络中最善于处理图片任务的是卷积神经网络。卷积神经网络包含多个小计算单元，以前馈方式分层次地处理视觉信息。如下图1所示。每一层的单元可以认为是图片过滤器的集合，每一个都会从输入图片中提取一个特定的特征。因此输出层也被称为特征映射：对输入图片进行不同的滤波。
当卷积神经网络用于物体识别的训练时，它们学习到的图片表达随着处理层次信息变得越来越清晰。因此，随着网络的处理层次，输入图片转换成的表达越来越关注实际的图片内容而不是具体像素值。我们可以通过从特征映射中重建图片直接可视化每层包含的输入图片的信息（如图1，可以了解下如何重建图片的方法细节）。网络中的高层捕获物体中的高层次信息，它们的分布在输入图片中，但是重建不限于精确的像素值。与之相反，低层重建只是简单地从原图复制精确像素值。因此我们也称网络中的高层特征响应为内容表达。
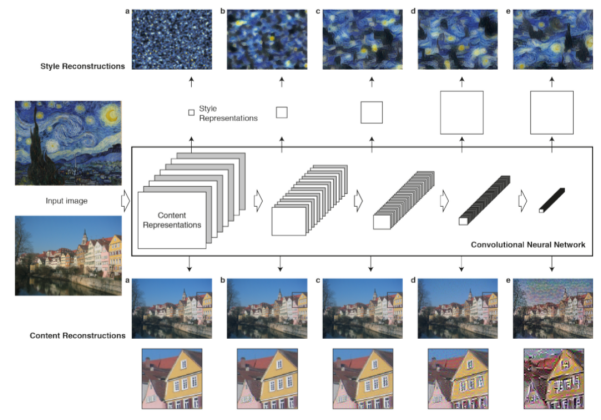
为了获得输入图片的风格表达，我们使用最初设计的特征空间来捕获纹理信息。这个特征空间建立在网络中每一层的滤波器响应之上。它由不同过滤器响应在特征映射空间的相关性组成。通过包含多个层的特征相关性，我们获得了对于输入图片固定的，多尺寸的表达，它捕获到了纹理信息而不是全局分布。
我们能够通过建立与给定输入图片风格表达相匹配的图片来可视化这些建立在网络中不同层的风格特征空间捕获到的信息。实际上从风格特征中重建出了输入图片的纹理版本，它捕获了色彩和局部结构的综合表现。不仅如此，来自输入图像的局部图像结构的大小和复杂度也随着层次增加，这个是因为感受野的尺寸和特征复杂度在增加。我们称这种多尺寸的表达为风格表达。
这篇论文主要是发现了卷积神经网络的内容和风格是可以分割的。我们可以独立操纵表达来产生一个新的，感知上有意义的图片。为了演示这个发现，我们从两个不同的源图片生成了混合内容和风格表达的图片。如下图2所示，我们将描述“Neckarfront”的内容表达与一些不同时期有名的艺术作品相匹配。
这些图片通过寻找同时匹配照片内容表达与艺术作品风格表达的图片进行合成。虽然原始图片的全局分布被保存，但是构成全局的颜色和局部结构由艺术作品提供。实际上这使图片呈现出艺术风格，虽然内容是相同的，但是合成图片看起来像艺术图片。
如以上总结的，风格表达是个多尺寸的表达，包含神经网络的多个层。如上图2所示，风格表达包含来自全部网络层次的层。也可以仅仅包含少量的较低层定义一个更加局部的风格，这会带来不同的视觉体验，如下图3所示。当匹配网络中更高层的风格表达时，局部图片结构与更大的尺寸匹配，这会带来更细致连续的视觉感受。事实上，视觉上更吸引人的图片通常是与网络中最高层的风格表达匹配得来的。
当然，图片内容与风格不能完全分离。当结合不同图片的内容和风格合成新图片时，往往不存在一个图片完全同时匹配两种约束。然而，我们在图片合成时最小化的loss函数分别包含内容和风格两方面，它们很好地分隔开。我们因此可以顺利地调整侧重点，是选择注重重建内容还是风格。当过分强调风格时会导致图片与艺术作品的外貌相匹配，而看不清任何照片内容（下图3第1列）。当过分强调内容时，我们能够很清楚辨认图片，但是绘画风格又没有很好匹配（图3最后一列）。对于一个特定原图片对，我们可以调整比例来产生视觉上有吸引力的图片。
这里我们提出了一个人工神经网络实现了图片内容和风格的分离，因此允许使用任何另一张图片的风格来重铸图片内容。我们通过创建新的艺术图片来展示这点，它结合了一些有名的绘画风格与任意选择的图片内容。实际上，我们从用于目标识别的深层神经网络的特征响应中推导出了图片内容和风格的神经表达。据我们所知，这是第一次在整体的自然图片中展示图片内容与风格特征的分离。此前内容和风格上的分割工作的评估在一些复杂程度低得多的感官输入上进行，比如不同的手写字体或者不同姿态的人脸和小图片。
在演示中，我们以一系列著名的艺术作品风格来渲染一张照片。这个问题通常是一个计算机视觉的分支，称为非光性渲染。概念上最密切相关的方法是使用纹理转换达到艺术风格转换。然而，此前的这些方法主要依赖于非参数的技术直接操纵图像的像素表达。与之相反，使用在目标检测上训练的深层神经网络时，我们是在特征空间进行操作，它们明确表达了一张图片的高层次的内容。
在目标检测任务上训练的深层神经网络的特征此前已被用于风格识别，为的是根据艺术作品创作的时间进行分类(论文[20])。这里的分类器在原始网络响应的最顶端进行训练，被称为是内容表达。我们推测一个转换成一个固定的空间，所以我们的风格表达可能在风格分类中达到一个更好的表现。
总的来说，我们合成图片的方法从不同来源混合了内容和风格。提供了新的，有吸引力的工具来研究一般的艺术，风格，内容独立的图片外观的感知和神经表现。我们可以设计新的刺激引入两个独立的，感知上有意义的差异来源：图片外观和图片内容。我们设想这将在广泛有关视觉感知的实验研究上发挥作用，涉及心理物理学，功能成像甚至是电生理神经记录。实际上，我们的工作提供了一个算法理解神经表达如何独立捕捉图片的内容和风格。重要的是，数学上我们的风格表达生成了一个清晰，可验证的hypothesis，关于图片外观的表达下达到了单个神经元的层面。风格表达简单计算网络中不同类型神经元之间的联系。计算神经元之间的联系在生物上是一个合理的运算，例如在主视觉系统中，这一功能被所谓的复杂细胞实现。我们的结果表明沿着流的方向在不同的处理阶段执行类似复杂细胞的运算或许是获得视觉输入外观内容独立表达的一种可能方法。
总而言之这是一个令人着迷的神经系统，它被训练去执行一个生物视觉的核心计算任务，自动学习图片表达，能够允许图片内容和风格分离。可能的解释是当学习目标识别时，网络已经保存了目标个体而对所有图片变异具有不变性。将图片内容和外观进行分解的表示，对于这项任务是很实际的。因此，我们从风格中抽象内容的能力，创造和享受艺术的能力，可能是我们视觉系统强大推理能力的主要特征。
Method:
在主要文本中生成的结果是基于VGG网络的，它是一个卷积神经网络，在通用的视觉目标识别任务上取得了和人类表现相当的结果，被广泛使用。我们使用拥有16个卷积和5个池化层的VGG网络提供的特征空间。我们没有使用任何全连接层。这个模型是公开可获取的，可以在caffe-framework中获得。对于图片合成我们发现将最大池化替换为平均池化改善了梯度流动可以获得更吸引人的效果，这就是为什么展示的生成图片是使用平均池化的原因。网络中每一层定义了一组非线性的滤波器，它们的复杂度随着层在网络中的位置增加。因此给定一个输入图片
在CNN中每一层都被滤波器的响应编码。一个拥有
个不同过滤器的层拥有大小为
的
个特征映射，这里的
等于特征映射的高度乘以宽度。所以l层的响应可以存储在矩阵
，这里
是指在l层，位置j处的第i个过滤器。所以当原始图片为
时，l层的特征表达分别为
。然后我们定义两个特征表达的平方差：
在l层的loss相对响应梯度为：
这样我们能够使用标准的后向传播流程计算相对于图片
的梯度。我们能够改变初始随机图片
直到它在特定层产生和原始图片
相同的响应。图1中的5个内容重建来源于原始VGG网络的conv1_1（a）,conv2_1(b),conv3_1(c),conv4_1(d)和conv5_1(e)层。
在网络中每一层CNN响应的顶端我们建立了一个风格表达来计算不同滤波器响应之间的相关性，期望对输入图片进行空间扩展。这里的特征相关性由Gram矩阵
表示，这里的
是l层向量化的特征映射i和j的内积
为了生成的纹理与给定图片相同（图1，风格重建），我们使用图片梯度从白噪声图片寻找另一张图片与原始图片的风格表达匹配。这是通过最小化原始图片和生成图片间Gram矩阵平均平方距离实现的。所以当
分别代表原始图片和生成图片时，
分别代表l层的风格表达。这一层对于总体loss的贡献为：
整体loss为：
这里的
是每一层对于总体loss的权重(下面给出了我们结果中
的特定值)。
相对于l层的响应的导数可以如下计算：
对应网络中低层响应的梯度可以使用使用标准的后向传播计算。图1中的5个风格重建生成是匹配conv1_1(a),conv1_1和conv2_1(b),conv1_1,conv2_1和conv3 _1(c),conv1_1,conv2_1,
conv3 _1 和conv4 _1(d), conv1_ 1, conv2_1, conv3_1, conv4 _1, 和conv5 _1(e)层的风格。
为了生成混合图片内容和绘画风格的图片，我们联合优化白噪声图片与网络中照片的一层内容表达与绘画中多层风格表达的距离。令
为照片，
为艺术作品。我们优化的loss函数为：
这里的
分别为内容和风格重建的比例。对于图2，我们的操作是匹配conv4_2的内容表达与conv1_1,conv2_1,conv3_1,conv4_1和conv5_1的风格表达（每一层的
，其他层的为0）。
的比例为
（图2的B,C,D）或
图2的E，F）。图3展示了使用不同内容和风格重建loss相对比例的效果，匹配的风格表达层分别为conv1_1(A),conv1_1和conv2_1(B), conv1_1,conv2_1和conv3_1(C), conv1_1, conv2_1, conv3_1和conv4_1(D),conv1_1, conv2_1,conv3_1,conv4_1和conv5_1(E)。因子
始终等于1除以非零loss权重的响应层数目。