判断两条直线是否相交,有两个步骤确定:
1、快速排斥。 2、跨立实验(啊啊啊,逼格好高)
然而事实解法的逼格却。。。
一 、快速排斥简单的说就是确保他们能相交的基本的要求是满足的:

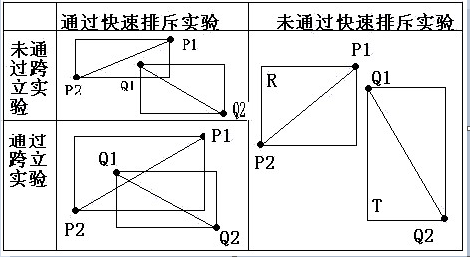
如上图,明显的,要两个线段相交,就要竖直方向有重叠(min(a.y, b.y) < max(d.y, c.y) && max(a.y, b.y) > min(d.y, c.y))
和水平方向有重叠(min(a.x, b.x) < max(c.x, d.x) && min(c.x, d.x) < max(a.x, b.x)); 觉得好low
二、跨立实验
如果两条线段相交,那么必须跨立,就是以一条线段为标准,另一条线段的两端点一定在这条线段的两端
用到叉积的知识,通过正负来判断一条线段两个点的相对位置;
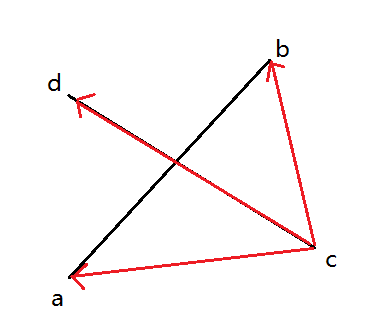
例如(ca x cd)·(cb x cd)<=0 则说明ca cb对于cd的方向不同,则a b在线段cd的两侧(明显由叉积定义可以知道一个是顺时针一个是逆时针,所以符号是不相同的)
贴上板子:
1 /***************************************线段相交模板****************************************/ 2 struct Point{//点 3 double x,y; 4 Point(){} 5 Point(int a,int b){//方便赋值 6 x=a; 7 y=b; 8 } 9 void input(){//定义输入函数方便用的时候 10 scanf("%lf%lf",&x,&y); 11 } 12 }; 13 struct Line{//线段 14 Point a,b; 15 Line(){} 16 Line(Point x,Point y){ 17 a=x; 18 b=y; 19 } 20 void input(){ 21 a.input(); 22 b.input(); 23 } 24 }; 25 bool judge(Point &a,Point &b,Point &c,Point &d) 26 { 27 /* 28 快速排斥: 29 两个线段为对角线组成的矩形,如果这两个矩形没有重叠的部分,那么两条线段是不可能出现重叠的 30 */ 31 if(!(min(a.x,b.x)<=max(c.x,d.x) && min(c.y,d.y)<=max(a.y,b.y)&&min(c.x,d.x)<=max(a.x,b.x) && min(a.y,b.y)<=max(c.y,d.y)))//这里的确如此,这一步是判定两矩形是否相交 32 //1.线段ab的低点低于cd的最高点(可能重合) 2.cd的最左端小于ab的最右端(可能重合) 33 //3.cd的最低点低于ab的最高点(加上条件1,两线段在竖直方向上重合) 4.ab的最左端小于cd的最右端(加上条件2,两直线在水平方向上重合) 34 //综上4个条件,两条线段组成的矩形是重合的 35 /*特别要注意一个矩形含于另一个矩形之内的情况*/ 36 return false; 37 /* 38 跨立实验: 39 如果两条线段相交,那么必须跨立,就是以一条线段为标准,另一条线段的两端点一定在这条线段的两段 40 也就是说a b两点在线段cd的两端,c d两点在线段ab的两端 41 */ 42 double u,v,w,z;//分别记录两个向量 43 u=(c.x-a.x)*(b.y-a.y)-(b.x-a.x)*(c.y-a.y); 44 v=(d.x-a.x)*(b.y-a.y)-(b.x-a.x)*(d.y-a.y); 45 w=(a.x-c.x)*(d.y-c.y)-(d.x-c.x)*(a.y-c.y); 46 z=(b.x-c.x)*(d.y-c.y)-(d.x-c.x)*(b.y-c.y); 47 return (u*v<=0.00000001 && w*z<=0.00000001); 48 } 49 50 /***************************************线段相交模板****************************************/