浅谈二维线段树

一、定义

二维线段树，即用线段树维护一个矩阵

有两种实现方式：

1、原一维线段树的基础上，每一个节点都是一个线段树，代表第二维

下图是一个4*4矩阵

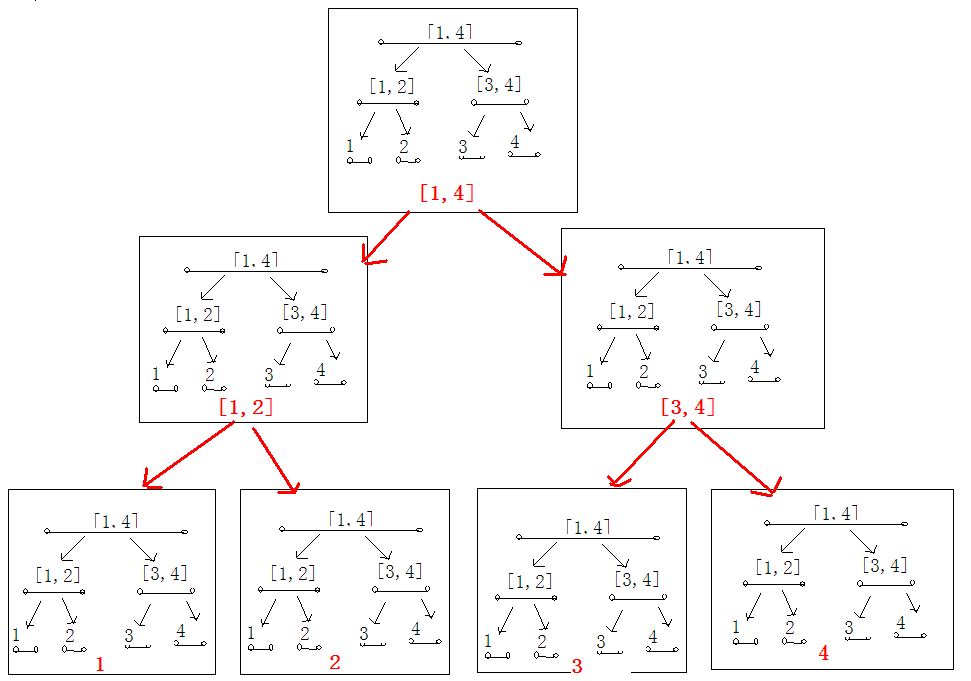
2、四分法转化为一维线段树

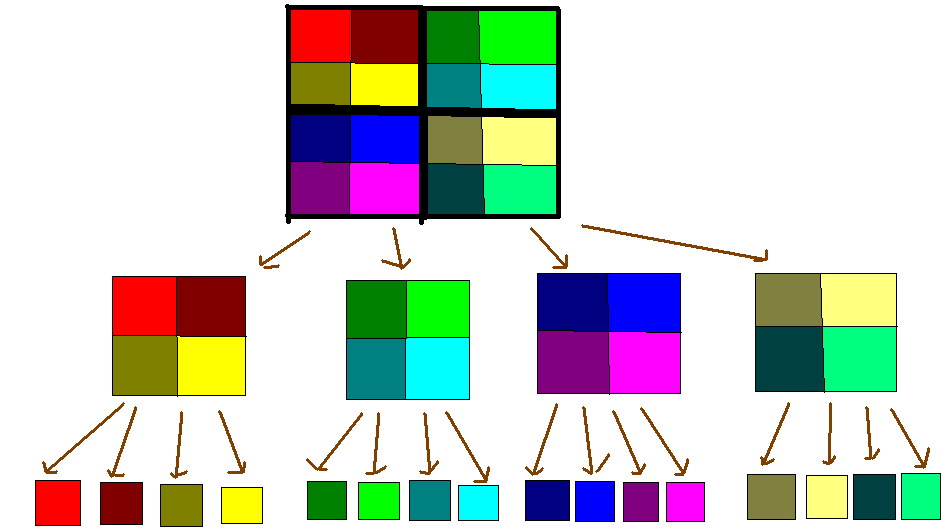
两种方法的空间复杂度都是n*n*log^2

第一种方法单次操作的时间复杂度是log^2，第二种方法最差可以退化到n

一维线段树的标记思想，在第一种方法中，可以用于二维线段树的第二维，不可以用于二维线段树的第一维

第二种方法本质上是四叉的一维线段树，

在此只介绍第一种方法

二、基本操作

1、单点修改+矩阵查询

单次访问一个位置，查询一个矩阵的总访问次数

访问位置（x，y）

所有第一维包含x的都包含位置（x，y），访问次数都要加1

所以从根到找到第一维包含x所经过的所有节点，在里面找到第二维包含y的节点，访问次数加1

sum[i][j] 表示的是这个节点所包含的矩阵的所有位置的访问次数之和

第一维：

void changex(int kx,int l,int r)
{
    changey(kx,1,1,h);
    if(l==r) return;
    int mid=l+r>>1;
    if(x<=mid) changex(kx<<1,l,mid);
    else changex(kx<<1|1,mid+1,r);
}

对于第二维的修改有两种写法

①、从根往下找经过的节点 f访问次数全部+1

因为此时已经确定了第一维包含，从根往下找y，所经过的区间一定包含y

void changey(int kx,int ky,int l,int r)
{
    sum[kx][ky]++;
    if(l==r) return;
    int mid=l+r>>1;
    if(y<=mid) changey(kx,ky<<1,l,mid);
    else changey(kx,ky<<1|1,mid+1,r);
}

②、在第二维中找到y，访问次数+1，祖先节点通过左右子节点的合并修改

void changey(int kx,int ky,int l,int r)
{
    if(l==r)
    {
        sum[kx][ky]++;
        return;
    }
    int mid=l+r>>1;
    if(y<=mid) changey(kx,ky<<1,l,mid);
    else changey(kx,ky<<1|1,mid+1,r);
    sum[kx][ky]=sum[kx][ky<<1]+sum[kx][ky<<1|1];
}

查询：

查询左上角为（xl，yl），右下角为（xr，yr）的矩阵的所有位置的访问次数之和

void queryy(int kx,int ky,int l,int r)
{
    if(l>=yl && r<=yr)
    {
        cnt+=sum[kx][ky];
        return;
    }
    int mid=l+r>>1;
    if(yl<=mid) queryy(kx,ky<<1,l,mid);
    if(yr>mid) queryy(kx,ky<<1|1,mid+1,r);
}

void queryx(int kx,int l,int r)
{
    if(l>=xl && r<=xr)
    {
        queryy(kx,1,1,h);
        return;
    }
    int mid=l+r>>1;
    if(xl<=mid) queryx(kx<<1,l,mid);
    if(xr>mid) queryx(kx<<1|1,mid+1,r);
}

2、矩阵修改+单点查询

修改

访问左上角为（x1，y1），右下角为（x2，y2）的矩阵

sum[i][j] 表示的是这个节点所代表的矩阵的整体访问次数

即这个矩阵的每一个位置都会有一个sum[i][j]的访问次数

void changey(int kx,int ky,int l,int r)
{
    if(y1<=l&&r<=y2)
    {
        sum[kx][ky]++;
        return;
    }
    int mid=l+r>>1;
    if(y1<=mid) changey(kx,ky<<1,l,mid);
    if(y2>mid) changey(kx,ky<<1|1,mid+1,r);
}
void changex(int kx,int l,int r)
{
    if(x1<=l&&r<=x2)
    {
        changey(kx,1,1,n);
        return;
    }
    int mid=l+r>>1;
    if(x1<=mid) changex(kx<<1,l,mid);
    if(x2>mid) changex(kx<<1|1,mid+1,r);
}

查询

查询位置（x，y）的访问次数

因为sum[i][j] 表示的是一个矩阵的整体访问次数，所以找（x，y）经过的所有点都要累计其访问次数

void queryy(int kx,int ky,int l,int r)
{
    ans+=sum[kx][ky];
    if(l==r) return;
    int mid=ly+ry>>1;
    if(y<=mid) queryy(kx,ky<<1,l,mid);
    else queryy(kx,ky<<1|1,mid+1,r);
}
void queryx(int kx,int l,int r)
{
    queryy(kx,1,1,n);
    if(l==r) return;
    int mid=l+r>>1;
    if(x<=mid) queryx(kx<<1,l,mid);
    else queryx(kx<<1|1,mid+1,r);
}

这两个sum[][] 含义不同，是为了适应不同的修改方式

一个是单点修改，一个是矩阵修改

而且矩阵修改不带标记下传