期望得分:100+60+30=190
实际得分:70+60+30=160
https://www.luogu.org/problem/lists?name=&orderitem=pid&tag=83%7C31
T1 无线网络发射器选址
题目描述
随着智能手机的日益普及,人们对无线网的需求日益增大。某城市决定对城市内的公共场所覆盖无线网。
假设该城市的布局为由严格平行的129 条东西向街道和129 条南北向街道所形成的网格状,并且相邻的平行街道之间的距离都是恒定值 1 。东西向街道从北到南依次编号为0,1,2…128 , 南北向街道从西到东依次编号为0,1,2…128 。
东西向街道和南北向街道相交形成路口,规定编号为x 的南北向街道和编号为y 的东西向街道形成的路口的坐标是(x , y )。 在 某 些 路口存在一定数量的公共场所 。
由于政府财政问题,只能安装一个大型无线网络发射器。该无线网络发射器的传播范围
一个以该点为中心,边长为2*d 的正方形。传播范围包括正方形边界。
例如下图是一个d = 1 的无线网络发射器的覆盖范围示意图。
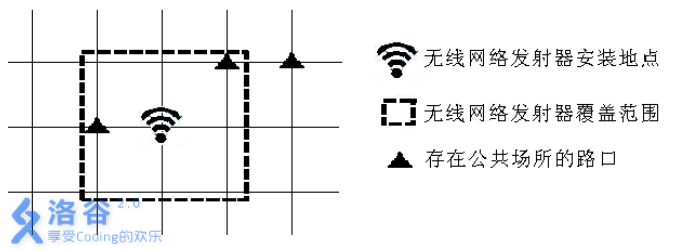
现在政府有关部门准备安装一个传播参数为d 的无线网络发射器,希望你帮助他们在城市内找出合适的安装地点,使得覆盖的公共场所最多。
输入输出格式
输入格式:
输入文件名为wireless.in。
第一行包含一个整数d ,表示无线网络发射器的传播距离。
第二行包含一个整数n ,表示有公共场所的路口数目。
接下来n 行,每行给出三个整数x , y , k , 中间用一个空格隔开,分别代表路口的坐标( x , y )
以及该路口公共场所的数量。同一坐标只会给出一次。
输出格式:
输出文件名为wireless.out 。
输出一行,包含两个整数,用一个空格隔开,分别表示能覆盖最多公共场所的安装地点 方案数,以及能覆盖的最多公共场所的数量。
输入输出样例
1 2 4 4 10 6 6 20
1 30
说明
对于100%的数据,1≤d≤20,1≤n≤20, 0≤x≤128,0≤y≤128,0<k≤1,000,000。
可以暴力枚举
但我搞了个二维前缀和
但。。70
原因是发射器覆盖范围可以超过边界
所以不能枚举覆盖范围的角,枚举安装位置
枚举角是想着少枚举几次,
对覆盖的最多公共场所没有影响,但对方案数有影响
因小失大
AC代码:

#include<cstdio> #include<algorithm> using namespace std; int d,n,x,y,k,tot; long long a[135][135],sum[135][135],ans,tmp; int main() { freopen("wireless.in","r",stdin); freopen("wireless.out","w",stdout); scanf("%d%d",&d,&n); for(int i=1;i<=n;i++) { scanf("%d%d%d",&x,&y,&k); a[y+1][x+1]=k; } for(int i=1;i<=129;i++) for(int j=1;j<=129;j++) sum[i][j]=sum[i-1][j]+sum[i][j-1]-sum[i-1][j-1]+a[i][j]; int x1,y1,x2,y2; for(int i=1;i<=129;i++) for(int j=1;j<=129;j++) { x1=i-d;y1=j-d; x2=i+d; y2=j+d; if(x1<1) x1=1; if(y1<1) y1=1; if(x2>129) x2=129; if(y2>129) y2=129; tmp=sum[x2][y2]-sum[x1-1][y2]-sum[x2][y1-1]+sum[x1-1][y1-1]; if(tmp>ans) { ans=tmp; tot=1;} else if(tmp==ans) tot++; } printf("%d ",tot); printf("%lld",ans); }
T2 寻找道路
题目描述
在有向图G 中,每条边的长度均为1 ,现给定起点和终点,请你在图中找一条从起点到终点的路径,该路径满足以下条件:
1 .路径上的所有点的出边所指向的点都直接或间接与终点连通。
2 .在满足条件1 的情况下使路径最短。
注意:图G 中可能存在重边和自环,题目保证终点没有出边。
请你输出符合条件的路径的长度。
输入输出格式
输入格式:
输入文件名为road .in。
第一行有两个用一个空格隔开的整数n 和m ,表示图有n 个点和m 条边。
接下来的m 行每行2 个整数x 、y ,之间用一个空格隔开,表示有一条边从点x 指向点y 。
最后一行有两个用一个空格隔开的整数s 、t ,表示起点为s ,终点为t 。
输出格式:
输出文件名为road .out 。
输出只有一行,包含一个整数,表示满足题目᧿述的最短路径的长度。如果这样的路径不存在,输出- 1 。
输入输出样例
3 2 1 2 2 1 1 3
-1
6 6 1 2 1 3 2 6 2 5 4 5 3 4 1 5
3
说明
解释1:
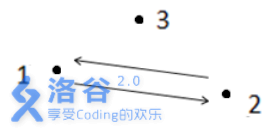
如上图所示,箭头表示有向道路,圆点表示城市。起点1 与终点3 不连通,所以满足题
目᧿述的路径不存在,故输出- 1 。
解释2:
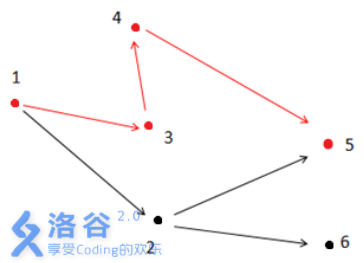
如上图所示,满足条件的路径为1 - >3- >4- >5。注意点2 不能在答案路径中,因为点2连了一条边到点6 ,而点6 不与终点5 连通。
对于30%的数据,0<n≤10,0<m≤20;
对于60%的数据,0<n≤100,0<m≤2000;
对于100%的数据,0<n≤10,000,0<m≤200,000,0<x,y,s,t≤n,x≠t。
筛选出 满足 “所有点的出边所指向的点都直接或间接与终点连通” 的点
然后跑最短路即可
问题在于如何筛选?
利用floyed求传递闭包可以 O(n³) 60分
100分方法:
如果从起点可以到终点,那么从终点沿反向边也可以到起点
所以可以对原图建立一张反向图,即将所有的边反向
从终点开始bfs,能遍历到的点,即为与终点连通的点
因为还要满足出边所指向的点 都要与终点联通
所以 如果一个点不能从终点便利到,删去反向图中,它直接相连的点
那么剩下的点 就是满足条件的
在这些点中 从起点在原图中再来一遍bfs即可
这就是正难则反思想
AC代码:

#include<cstdio> #include<cstring> #include<queue> #define M 200001 #define N 10001 using namespace std; int n,m,s,t; int front[N],front_[N],to[M],to_[M],nextt[M],nextt_[M],tot,tot_; bool v_[N],in[N],use[N]; int dis[N]; queue<int>q; void add(int u,int v) { to[++tot]=v; nextt[tot]=front[u]; front[u]=tot; } void add_(int u,int v) { to_[++tot_]=v; nextt_[tot_]=front_[u]; front_[u]=tot_; } int main() { freopen("roadb.in","r",stdin); freopen("roadb.out","w",stdout); scanf("%d%d",&n,&m); int x,y; while(m--) { scanf("%d%d",&x,&y); add(x,y); add_(y,x); } scanf("%d%d",&s,&t); q.push(t); v_[t]=true; int now; while(!q.empty()) { now=q.front(); q.pop(); for(int i=front_[now];i;i=nextt_[i]) if(!v_[to_[i]]) { v_[to_[i]]=true; q.push(to_[i]);} } memset(use,1,sizeof(use)); for(int i=1;i<=n;i++) if(!v_[i]) { use[i]=false; for(int j=front_[i];j;j=nextt_[j]) use[to_[j]]=false; } if(!use[s]) { printf("-1");return 0;} memset(dis,-1,sizeof(dis)); q.push(s); in[s]=true; dis[s]=0; while(!q.empty()) { now=q.front(); q.pop(); in[now]=false; for(int j=front[now];j;j=nextt[j]) if(use[to[j]]&&!in[to[j]]&&dis[to[j]]==-1) { dis[to[j]]=dis[now]+1; q.push(to[j]); in[to[j]]=true;} } printf("%d",dis[t]); }
60分代码:

#include<cstdio> #include<cstring> using namespace std; int n,m,s,t; int edge[1001][1001]; bool f[1001][1001]; int g[1001][1001]; int main() { freopen("roadb.in","r",stdin); freopen("roadb.out","w",stdout); scanf("%d%d",&n,&m); int x,y; for(int i=1;i<=m;i++) { scanf("%d%d",&x,&y); if(x!=y) { f[x][y]=true; edge[x][++edge[x][0]]=y; } } scanf("%d%d",&s,&t); for(int i=1;i<=n;i++) f[i][i]=true; for(int k=1;k<=n;k++) for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) if(f[i][k]&&f[k][j]) f[i][j]=true; memset(g,-1,sizeof(g)); for(int i=1;i<=n;i++) g[i][i]=0; bool ok; for(int i=1;i<=n;i++) { ok=true; if(f[i][t]) for(int j=1;j<=edge[i][0];j++) if(!f[edge[i][j]][t]) { ok=false; break;} if(ok) for(int j=1;j<=edge[i][0];j++) g[i][edge[i][j]]=1; } for(int k=1;k<=n;k++) for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) if(g[i][k]!=-1&&g[k][j]!=-1&&(g[i][j]==-1||g[i][j]>g[i][k]+g[k][j])) g[i][j]=g[i][k]+g[k][j]; printf("%d",g[s][t]); }
考试时判断联通的想法:
终点向起点连一条边,
若点与终点连通,那么它必在起点与终点形成的环中
然后tarjer 判环,只保留起点的环中节点
正确性仍待验证
但有一个跟写满分做法时相同的错误:
点是否与终点连通、点是否符合条件 混用一个数组
若点i不与终点连通,那么就要删去有边直接指向它的点j
如果用同一数组,相当于把这个点j标记为与终点不连通
那么就要删去有边指向点j的点k
但有可能点j与终点连通,点k符合条件
也就是 若i<-j<-k,若i不合法,则j不合法,但k可能合法
即不合法性没有传递性
T3 解方程
题目描述
已知多项式方程:
a0+a1x+a2x^2+..+anx^n=0
求这个方程在[1, m ] 内的整数解(n 和m 均为正整数)
输入输出格式
输入格式:
输入文件名为equation .in。
输入共n + 2 行。
第一行包含2 个整数n 、m ,每两个整数之间用一个空格隔开。
接下来的n+1 行每行包含一个整数,依次为a0,a1,a2..an
输出格式:
输出文件名为equation .out 。
第一行输出方程在[1, m ] 内的整数解的个数。
接下来每行一个整数,按照从小到大的顺序依次输出方程在[1, m ] 内的一个整数解。
输入输出样例
2 10 1 -2 1
1 1
2 10 2 -3 1
2 1 2
2 10 1 3 2
0
说明
30%:0<n<=2,|ai|<=100,an!=0,m<100
50%:0<n<=100,|ai|<=10^100,an!=0,m<100
70%:0<n<=100,|ai|<=10^10000,an!=0,m<10000
100%:0<n<=100,|ai|<=10^10000,an!=0,m<1000000
考试时 只打了30的暴力
思路已有正解的萌芽,但由于本着第二题应该比第三题好做的思维定势
耗费时间做了第二题
然后时间就不够了
正解:
0模任何数都等于0
考虑方程在剩余系意义下的解
选取质数p
若左边%p=0,则x是方程的解
但可能存在左边是p的倍数的情况,
所以选2个质数,不放心的话可以在多选几个
如何处理读入的高精度?
将系数以类似于读入优化的方式,边读入,边%p

#include<cstdio> #include<cstring> using namespace std; int n,m,len,tot; char s[10010]; long long a[3][101],p[3],tmp,w; bool anti; bool b[1000001]; void turn(int k) { len=strlen(s); int j,g; if(s[0]=='-') { anti=true; g=1; } else { anti=false; g=0; } for(int i=1;i<=2;i++) { j=g; for(;j<len;j++) a[i][k]=(a[i][k]*10%p[i]+s[j]-'0')%p[i]; if(anti) a[i][k]=p[i]-a[i][k]; } } bool check(int x,int k) { tmp=0;w=1; for(int i=0;i<=n;i++) { tmp=(tmp+a[k][i]*w%p[k])%p[k]; w=w*x%p[k]; } return tmp; } int main() { p[1]=22861;p[2]=1000007977; scanf("%d%d",&n,&m); for(int i=0;i<=n;i++) { scanf("%s",s); turn(i); } for(int i=1;i<=p[1];i++) { if(check(i,1)) continue; for(int j=i;j<=m;j+=p[1]) if(!check(j,2)) b[j]=true,tot++; } printf("%d ",tot); for(int i=1;i<=m;i++) if(b[i]) printf("%d ",i); }
一个错误:
for(int i=1;i<=p[1];i++)
{
if(check(i,1)) continue;
for(int j=i;j<=m;j+=p[1])
if(!check(j,2)) b[j]=true,tot++;
}
当时写的是:
for(int i=1;i<=p[1];i++)
{
if(check(i,1)) continue;
for(int j=i;j<=m;j+=p[1])
if(!check(j,2)) b[++b[0]]=j;
}
自以为优化了循环统计个数的过程
缺陷:不能保证b数组升序
本次考试总有一些错误的优化
但其实也优化不了多少
反而因小失大
优化之前要慎重
比较有价值的东西:正难则反思想
