巧克力棒(chocolate)
Time Limit:1000ms Memory Limit:64MB
题目描述
LYK 找到了一根巧克力棒,但是这根巧克力棒太长了,LYK 无法一口吞进去。
具体地,这根巧克力棒长为 n,它想将这根巧克力棒折成 n 段长为 1 的巧克力棒,然后
慢慢享用。
它打算每次将一根长为 k 的巧克力棒折成两段长为 a 和 b 的巧克力棒,此时若 a=b,则
LYK 觉得它完成了一件非常困难的事,并会得到 1 点成就感。
LYK 想知道一根长度为 n 的巧克力棒能使它得到最多几点成就感。
输入格式(chocolate.in)
第一行一个数 n。
输出格式(chocolate.out)
一个数表示答案。
输入样例
7
输出样例
4
数据范围
对于 20%的数据 n<=5。
对于 50%的数据 n<=20。
对于 80%的数据 n<=2000。
对于 100%的数据 n<=1000000000。
样例解释
将 7 掰成 3+4, 将 3 掰成 1+2, 将 4 掰成 2+2 获得 1 点成就感, 将剩下的所有 2 掰成 1+1
获得 3 点成就感。总共 4 点成就感。
思路:容易看出,要将一个数分解成1,那么必然涉及到二进制(与2有关啊)。
根据二进制的性质,容易看出,一个数二进制含有1的个数就是不能分解成$2^n$的次数。
所以只需要统计出这个数二进制中1的个数,然后就没有然后了。
代码:

#include<cstdio> using namespace std; int n; int main() { freopen("chocolate.in","r",stdin); freopen("chocolate.out","w",stdout); scanf("%d",&n); printf("%d",n-__builtin_popcount(n)); fclose(stdin); fclose(stdout); return 0; }
2333...时间复杂度大约是$O(log n)$.
LYK 快跑!(run)
Time Limit:5000ms Memory Limit:64MB
题目描述
LYK 陷进了一个迷宫! 这个迷宫是网格图形状的。 LYK 一开始在(1,1)位置, 出口在(n,m)。
而且这个迷宫里有很多怪兽,若第 a 行第 b 列有一个怪兽,且此时 LYK 处于第 c 行 d 列,此
时这个怪兽对它的威胁程度为|a-c|+|b-d|。
LYK 想找到一条路径,使得它能从(1,1)到达(n,m),且在途中对它威胁程度最小的怪兽的
威胁程度尽可能大。
当然若起点或者终点处有怪兽时,无论路径长什么样,威胁程度最小的怪兽始终=0。
输入格式(run.in)
第一行两个数 n,m。
接下来 n 行,每行 m 个数,如果该数为 0,则表示该位置没有怪兽,否则存在怪兽。
数据保证至少存在一个怪兽。
输入格式(run.out)
一个数表示答案。
输入样例
3 4
0 1 1 0
0 0 0 0
1 1 1 0
输出样例
1
数据范围
对于 20%的数据 n=1。
对于 40%的数据 n<=2。
对于 60%的数据 n,m<=10。
对于 80%的数据 n,m<=100。
对于 90%的数据 n,m<=1000。
对于另外 10%的数据 n,m<=1000 且怪兽数量<=100。
思路分析:这题时间限制5s...看起来非常美妙。
容易看出,可以以每一个怪兽为起点进行BFS,预处理每一个点到最近的怪兽的距离。然后进行二分答案,在确保路径可行(联通)的情况下二分。

#include<cstdio> #include<cstring> #include<queue> #define maxn 1010 using namespace std; int n,m,l,r,ans; int dis[maxn][maxn],f[maxn][maxn]; int b[5]= {0,0,1,0,-1}; int c[5]= {0,1,0,-1,0}; struct edge { int x,y; }; queue<edge>q; inline void bfs()//update the distance to the monster foreach point nearby. { while(!q.empty()) { int nx=q.front().x; int ny=q.front().y; q.pop(); for(int i=1; i<=4; i++) { int tx=nx+b[i]; int ty=ny+c[i]; if(tx>=1&&tx<=n&&ty>=1&&ty<=m&&!f[tx][ty]) { f[tx][ty]=1; dis[tx][ty]=dis[nx][ny]+1; edge nxt; nxt.x=tx,nxt.y=ty; q.push(nxt); } } } } inline int judge(int x)//judge for binary search { if(dis[1][1]<x)return 0;//if the distance to the nearest monster of the start point < mid, return fail. //that means, the distance to the nearest monster of the start point should be smaller than mid. for(int i=1; i<=n; i++)//clear the visited array for(int j=1; j<=m; j++) f[i][j]=0; while(!q.empty())//clear the queue q.pop(); edge tmp; tmp.x=1,tmp.y=1; q.push(tmp); f[1][1]=1; while(!q.empty()) { int nx=q.front().x; int ny=q.front().y; q.pop(); if(nx==n&&ny==m)//if get to the end point,return success. return 1; for(int i=1; i<=4; i++) { int tx=nx+b[i]; int ty=ny+c[i]; if(tx>=1&&tx<=n&&ty>=1&&ty<=m&&dis[tx][ty]>=x&&!f[tx][ty]) { f[tx][ty]=1; edge t; t.x=tx,t.y=ty; q.push(t); } } } return 0; } inline void bin() { l=0,r=3000; while(l<=r) { int mid=(l+r)/2; if(judge(mid)) { ans=mid; l=mid+1; } else r=mid-1; } printf("%d ",ans); } int main() { freopen("run.in","r",stdin); freopen("run.out","w",stdout); scanf("%d",&n); scanf("%d",&m); memset(dis,127/3,sizeof(dis)); for(int i=1; i<=n; i++) { for(int j=1; j<=m; j++)//readin every point { int x; scanf("%d",&x); if(x==1)//if this is a monster, foreach monster, do search. { dis[i][j]=0; edge cur; cur.x=i,cur.y=j; q.push(cur); f[i][j]=1; } } } bfs(); bin();//binary_search for the answer. fclose(stdin); fclose(stdout); return 0; }
仙人掌(cactus)
Time Limit:1000ms Memory Limit:64MB
题目描述
LYK 在冲刺清华集训(THUSC) !于是它开始研究仙人掌,它想来和你一起分享它最近
研究的结果。
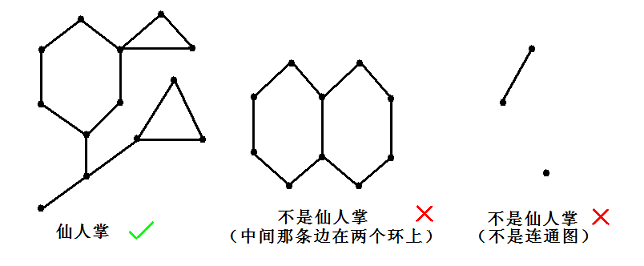
如果在一个无向连通图中任意一条边至多属于一个简单环 (简单环的定义为每个点至多
经过一次) ,且不存在自环,我们称这个图为仙人掌。
LYK 觉得仙人掌还是太简单了,于是它定义了属于自己的仙人掌。
定义一张图为美妙的仙人掌, 当且仅当这张图是一个仙人掌且对于任意两个不同的点 i,j,
存在一条从 i 出发到 j 的路径,且经过的点的个数为|j-i|+1 个。
给定一张 n 个点 m 条边且没有自环的图,LYK 想知道美妙的仙人掌最多有多少条边。
数据保证整张图至少存在一个美妙的仙人掌。
输入格式(cactus.in)
第一行两个数 n,m 表示这张图的点数和边数。
接下来 m 行,每行两个数 u,v 表示存在一条连接 u,v 的无向边。
输出格式(cactus.out)
一个数表示答案
输入样例
4 6
1 2
1 3
1 4
2 3
2 4
3 4
输出样例
4
样例解释
选择边 1-2,1-3,2-3,3-4,能组成美妙的仙人掌,且不存在其它美妙仙人掌有超过 4 条
边。
数据范围
对于 20%的数据 n<=3。
对于 40%的数据 n<=5。
对于 60%的数据 n<=8。
对于 80%的数据 n<=1000。
对于 100%的数据 n<=100000 且 m<=min(200000,n*(n-1)/2)。
solution: 观察美丽的仙人掌的定义,发现编号为i与i+1之间必存在一条边,问题转化成有若干区间,求最多的区间,使得区间之间没有重叠和覆盖。这个问题是可以直接贪心或者dp的。
思路分析:...gg...

#include<iostream> #include<cstdio> #include<algorithm> using namespace std; const int maxn=200010; int n,m,tot,ans; struct node { int x; int y; bool operator < (node tmp)const { return y<tmp.y; } }a[maxn*2]; int main() { freopen("cactus.in","r",stdin); freopen("cactus.out","w",stdout); int x,y; scanf("%d%d",&n,&m); for(int i=1;i<=m;i++) { scanf("%d%d",&x,&y); if(x>=y) swap(x,y); if(x+1==y) continue; a[++tot].x=x;a[tot].y=y; } sort(a+1,a+tot+1); int end=-1; for(int i=1;i<=tot;i++) if(a[i].x>=end) { end=a[i].y; ans++; } cout<<ans+n-1; fclose(stdin);fclose(stdin); return 0; }
