自动机理论的中心概念

字母表：

字母表是符号的有穷非空集合。用“Σ”符号表示字母表。常见的字母表包括：

1. Σ={0,1}，二进制字母表
2. Σ={a,b,...,z}，所有小写字母的集合

串：

串（有时候被称为单词）是从某个字母表中选择的符号的有穷序列。

空串：

空串是出现0次符号的串。这个串记作ε，是可以从任何字母表中选择的串。

串的长度：

串的长度，即串中的符号的位数。串的长度的标准记号是|w|。例如 |011|=3。

字母表的幂：

如果Σ是一个字母表，就可以用指数记号来表示这个字母表某个长度的所有串的集合。定义Σ^k是长度为k的串的集合，而串的每个符号属于Σ。

串的连接：

设x和y都是串。于是，xy表示x和y的连接，也就是说，用x的一个副本后面跟着y的一个副本所形成的串。

克莱尼星号：

设集合S是一个字符集合，则S*表示由这个字符集合中的字符组成的字符串集合。

语言：

Σ是某个具体的字母表，全都从Σ*中选出的串的某个集合表示语言。如果Σ是字母表，并且L是Σ*的子集，则L是Σ上的语言。注意，Σ上的语言不必包含带有Σ所有符号的串，所以一旦确定L是Σ上的语言，也就知道了L是任何是Σ超集（即包含集合Σ的集合）的字母表上的语言。

关于什么是语言，唯一重要的约束就是所有字母表都是有穷的。因此语言可以有无穷多个串，但限制这些串为从一个固定的有穷字母表中取出的。

问题：

在自动机理论中，一个问题就是判定一个给定的串是否是属于某个具体语言的提问。更准确地说，如果Σ是字母表，L是Σ上的语言，则问题L就是：

• 给定Σ*中的一个串w，判定w是否属于L。

集合表示法作为一种定义语言的方式，常用的“集合表示法”：{w|w如此这般}，来描述一个语言。这个表达式读作：“单词w的集合，使得w如此这般”

文法：

G=(V,T,P,S)，其中

• V表示非终止符集合，非终止符可以根据产生式生成符号。
• T表示终止符集合，终止符无法继续生成符号。
• P产生式，即非终止符产生符号的规则。
• S起始符，起始符就是非终止符结合中的一个元素。

文法的简写形式：

只写产生式，如果几个产生式的左端相同，则把右端的结果用”|“连接起来。第一个产生式的左端符号表示起始符。

文法推导：

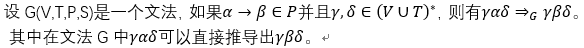
例如：

 

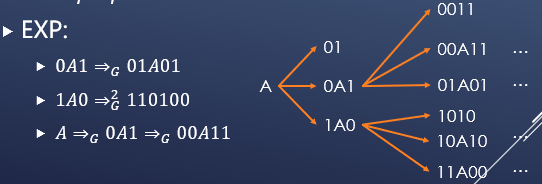
语言的文法定义：设G=(V,T,P,S)是一种文法，则由这种文法定义的语言定义为：

                    

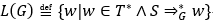
不同的推导类型：

• 最左推导：在推导过程中总是替换句子最左端的非终止符。
• 最右推导：在推导过程中总是替换句子最右端的非终止符。
• 任意推导：既不是最左推导也不是最右推导。

文法的分类：

不同类型文法的区分：

1型文法：1)产生式的左边可以有多个字符，但必须有一个非终结符

　　　　  2)产生式的右边，可以是终结符，也可以是非终结符，但必须是有限个字符

2型文法：1)产生式的左边只能有一个字符，而且是非终结符

　　　      2)产生式的右边，可以是终结符，也可以是非终结符，但必须是有限个字符

3型文法：1)产生式的左边只能有一个字符，而且是非终结符

　　　　  2)产生式的右边，最多只有两个字符：i：如果只有一个字符，那么必须是终结符

　　　　　　　　　　　　　　　　　　　　　 ii：如果有两个字符，那么一定是一个终结符和一个非终结符

3型文法包括左线形文法、右线形文法、正规文法：

左线形文法：产生式的右部要么没有非终结符，如果有非终结符也只能有一个，并且非终结符只能位于产生式右端的最左边

右线形文法：产生式的右部要么没有非终结符,如果有非终结符也只能有一个，并且非终结符只能位于产生式右端的最左边

正规文法：正规文法是右线形文法的一个子集，其产生式的右端只有三种情况：

1. 空串
2. 只有一个终结符
3. 只有一个终结符后接一个非终结符