C. AND Graph
time limit per test
4 secondsmemory limit per test
256 megabytesinput
standard inputoutput
standard outputYou are given a set of size mm with integer elements between 00 and 2n−12n−1 inclusive. Let's build an undirected graph on these integers in the following way: connect two integers xx and yy with an edge if and only if x&y=0x&y=0. Here && is the bitwise AND operation. Count the number of connected components in that graph.
Input
In the first line of input there are two integers nn and mm (0≤n≤220≤n≤22, 1≤m≤2n1≤m≤2n).
In the second line there are mm integers a1,a2,…,ama1,a2,…,am (0≤ai<2n0≤ai<2n) — the elements of the set. All aiai are distinct.
Output
Print the number of connected components.
Examples
input
Copy
2 3 1 2 3
output
Copy
2
input
Copy
5 5 5 19 10 20 12
output
Copy
2
Note
Graph from first sample:
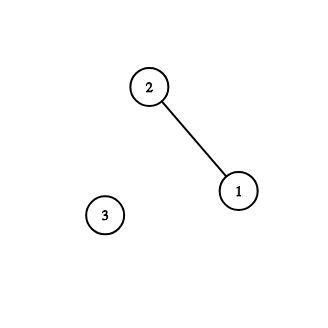
Graph from second sample:
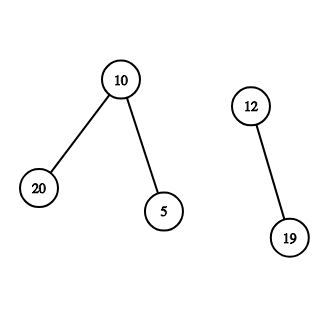
#include<iostream>
#include<cstring>
#include<cmath>
#include<cstdlib>
#include<cstdio>
#include<algorithm>
#include<string>
#include<map>
#include<queue>
#define ll long long
using namespace std;
int f[35];
int n,m,isp[5001000],a[5001000],vis[5001000],N,ans=0,i;
void dfs(int x)
{
// printf("%d %d
",x,i);
if(vis[x]==1) return ;
vis[x]=1;
if(isp[x]) dfs(N^x);
for(int i=1;i<=n;i++) if(x&(1<<(i-1))) dfs(x^(1<<(i-1)));
}
void solve()
{
for(int i=1;i<=m;i++)
if(!vis[a[i]])
{
ans++;
vis[a[i]]=1;
dfs(N^a[i]);
}
}
int main()
{
f[1]=1;
for(int i=2;i<=30;i++) f[i]=f[i-1]*2;
scanf("%d%d",&n,&m);
N=f[n+1]-1;
for(int i=1;i<=m;i++) scanf("%d",&a[i]);
for(int i=1;i<=m;i++) isp[a[i]]=1;
solve();
printf("%d
",ans);
} 
