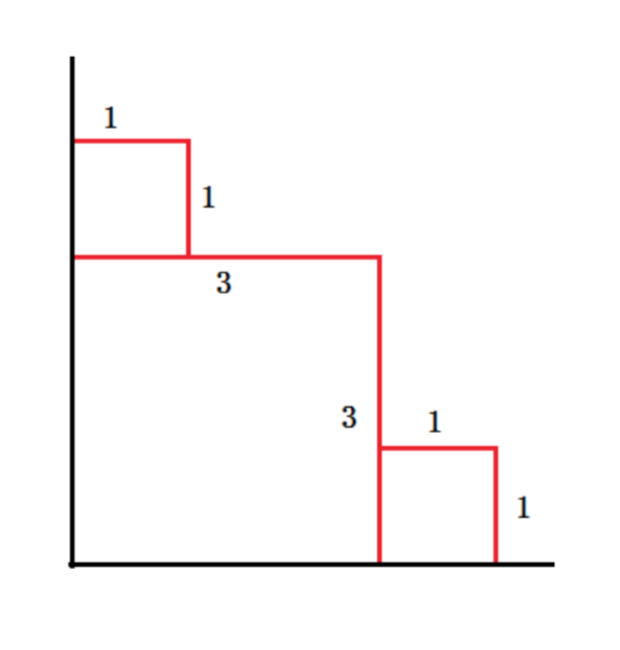
There's a beach in the first quadrant. And from time to time, there are sea waves. A wave ( xx , yy ) means the wave is a rectangle whose vertexes are ( 00 , 00 ), ( xx , 00 ), ( 00 , yy ), ( xx , yy ). Every time the wave will wash out the trace of former wave in its range and remain its own trace of ( xx , 00 ) -> ( xx , yy ) and ( 00 , yy ) -> ( xx , yy ). Now the toad on the coast wants to know the total length of trace on the coast after n waves. It's guaranteed that a wave will not cover the other completely.
Input
The first line is the number of waves n(n le 50000)n(n≤50000).
The next nn lines,each contains two numbers xx yy ,( 0 < x0<x , y le 10000000y≤10000000 ),the ii-th line means the ii-th second there comes a wave of ( xx , yy ), it's guaranteed that when 1 le i1≤i , j le nj≤n ,x_i le x_jxi≤xj and y_i le y_jyi≤yj don't set up at the same time.
Output
An Integer stands for the answer.
Hint:
As for the sample input, the answer is 3+3+1+1+1+1=103+3+1+1+1+1=10
样例输入复制
3 1 4 4 1 3 3
样例输出复制
10
题目来源
题意:每次海浪会产生两段轨迹,后面的海浪会前面的海浪轨迹覆盖掉,问最后剩余的轨迹长度
思路:我们从后往前考虑,最后一个海浪必定是完整的,之后的海浪增加的值是看集合里比他小的最大的数就是能覆盖掉他多少长度,减去这个长度就行。
即处理到(x[i],y[i])这个波浪增加的值是x[i]-max(x[j])(i+1<=j<=n,x[j]<x[i])+y[i]-max(y[i])(i+1<=j<=n,y[j]<y[i]),如果n比较小的话我们可以直接插排,复杂度是O(n²),不过我们可以用分块的思想来做,先离散一遍,确定每个点的最终位置,之后根号n的往前找<x[i]的最大值。复杂度O(n√n)
#include<iostream>
#include<cstring>
#include<cmath>
#include<cstdlib>
#include<cstdio>
#include<algorithm>
#include<string>
#include<map>
#include<queue>
#include<vector>
#include<stack>
#define ll long long
#define maxn 4001000
#define lson l,m,rt<<1
#define rson m+1,r,rt<<1|1
#define rep(i,a,b) for(int i=a;i<=b;i++)
const int P=1e9+7;
using namespace std;
struct node{
int x,y,id;
}a[101010];
int flag,unit,x[101010],y[101010],tx[101010],ty[101010],fx[101010],fy[101010],rx[101010],ry[101010],bx,by;
ll ans=0;
bool cmp1(node a,node b)
{
return a.x<b.x;
}
bool cmp2(node a,node b)
{
return a.y<b.y;
}
void check1(int i)
{
flag=0;
for(int j=rx[i]-1;j>=(bx-1)*unit;j--)
{
if(tx[j]!=-1)
{
ans+=x[i]-tx[j];
flag=1;
break;
}
}
if(!flag)
{
for(int j=bx-1;j>=1;j--)
{
if(fx[j]!=0)
{
for(int k=j*unit-1;k>=(j-1)*unit;k--)
{
if(tx[k]!=-1)
{
ans+=x[i]-tx[k];
break;
}
}
break;
}
}
}
}
void check2(int i)
{
flag=0;
for(int j=ry[i]-1;j>=(by-1)*unit;j--)
{
if(ty[j]!=-1)
{
ans+=y[i]-ty[j];
flag=1;
break;
}
}
if(!flag)
{
for(int j=by-1;j>=1;j--)
{
if(fy[j]!=0)
{
for(int k=j*unit-1;k>=(j-1)*unit;k--)
{
if(ty[k]!=-1)
{
ans+=y[i]-ty[k];
break;
}
}
break;
}
}
}
}
int n,m;
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++)
scanf("%d%d",&a[i].x,&a[i].y),x[i]=a[i].x,y[i]=a[i].y,a[i].id=i;
sort(a+1,a+1+n,cmp1);
for(int i=1;i<=n;i++) rx[a[i].id]=i;//rx[]表示x[i]的最终位置
sort(a+1,a+1+n,cmp2);
for(int i=1;i<=n;i++) ry[a[i].id]=i;
unit=sqrt(n);
fx[1]=fy[1]=1;//fx[i]为0表示x坐标第i块中没元素,1表示有元素
for(int i=1;i<=n;i++) tx[i]=ty[i]=-1;
for(int i=n;i>=1;i--)
{
bx=rx[i]/unit+1;by=ry[i]/unit+1;
check1(i);check2(i);
tx[rx[i]]=x[i];ty[ry[i]]=y[i];//tx[]表示点权
fx[bx]=1;fy[by]=1;
}
printf("%lld
",ans);
}