扩展阅读

拓展小阅读：图的 \(k\) 连通问题

学习参考：yhx的2021年国家集训队论文

1 特殊符号表示

\(V(G)\) 表示 \(G\) 的点集， \(E(G)\) 表示 \(G\) 的边集。

用 \(d(u)\) 表示 \(u\) 的度数，则最小度 \(\delta(G)=\min_{v\in G}d(v)\)， \(\Delta(G)=\max_{v\in G}d(u)\)。

对于图 \(G\) 的导出子图，用 \(G[V']\) 表示点集为 \(V'\) 的导出子图。

对于一对 \(u,v\)，若存在点集 $S\subseteq V\setminus {u,v} $ 使得割去 \(S\) 中所有的点使得 \(u,v\) 不连通，则称 \(S\) 为 \(u,v\) 的局部点割集，且 \(S\) 为 \(G\) 的一个全局点割集。定义 \(u,v\) 的局部点连通度 \(\kappa(u,v)\) 表示 \(\min |S_{u,v}|\)，\(G\) 的点连通度 \(\kappa(G)\) 为 \(\min_{(u,v)\notin E}\kappa(u,v)\)。当 \(G\) 是完全图时，需要另作讨论。

同样的，若存在边集 \(F\) 使得割去 \(F\) 中边使得 \(u,v\) 不连通，则称 \(F\) 为 \(u,v\) 的局部边割集，且 \(F\) 为 \(G\) 的一个全局边割集。定义 \(u,v\) 的局部边连通度 \(\lambda(u,v)\) 表示 \(\min |F_{u,v}|\)，\(G\) 的边连通度 \(\lambda(G)\) 为 \(\min_{u\neq v} \lambda(u,v)\)。当 \(|V(G)|=1\) 时，定义 \(\lambda(G)=+\infty\)。

2 基本性质

1. Menger 定理

   对于不相邻顶点 \(u,v\)，\(\kappa(u,v)\ge k\) 当且仅当存在 \(k\) 条 \(u,v\) 之间的点不交路径。

   对于任意顶点对 \(u,v\)，\(\lambda(u,v)\ge k\) 当且仅当存在 \(k\) 条 \(u,v\) 之间的边不交路径。

   利用这个定理，我们可以有一个 \(O(\text{Flow}(|V|,|E|))\) 的时间复杂度得到一对 \(u,v\) 的 \(\kappa(u,v)\) 和 \(\lambda(u,v)\)。

2. 一些界

   首先一个非常显的界，对于不相邻 \(u,v\) 有 \(\kappa(u,v)\le \lambda(u,v)\le \min\{d(u),d(v)\}\)，推广到整个图上有 \(\kappa(G)\le \lambda(G)\le \delta(G)\le \frac{2|E|}{|V|}\)。

   需要用这些东西分析复杂度呢 >_<。

3 边连通问题

我们称 \(u,v\) 为一对 \(k\) 边连通点对当且仅当 \(\lambda(u,v)\ge k\)。这种二元关系是 \(V\) 上的一个等价关系，于是我们可以将图划分成若干个等价类，对于每一个等价类，我们称其为一个 \(k\) 边连通分量。一个 \(k\) 边连通分量不一定是连通的。

边连通分量划分

首先，根据 Menger 定理，我们可以对所有 \(u,v\) 做一次网络流，然后判断出所有 \(u,v\) 是否为 \(k\) 边连通点对。这样做的复杂度为 \(O(|V|^2F)\)，其中 \(O(F)\) 代表一次网络流的复杂度。

实际上我们可以更好的利用求出的网络流的结果。我们每求一次网络流（最小割），若流量 \(<k\)，则实际上可以将图分成两半，而这两半都一定是若干个 \(k\) 连通分量的并。否则我们可以将两个点合并起来。具体而言：

1. 我们先找到任意一对 \(u_0,v_0\) 的最小局部边割集 \(F\)。
2. 若 \(|F|\ge k\)，那么 \(u_0,v_0\) 一定处于同一连通分量，合并起来即可，此时 \(|V|\) 会减少 \(1\)。然后回到 1。
3. 否则，我们找到割去 \(F\) 的边后，分成的两个连通块 \(C_u\) 和 \(C_v\)，并且 \(C_u\) 和 \(C_v\) 一定是互不相干的（即不存在分别来自这两个点集的两个点在同一 \(k\) 连通分量）。于是转化为一个子问题，对两个点集分别做 1 的操作。

于是总复杂度 \(O(|V|F)\)。

局部边连通度查询 / 最小割树

解决这个问题的办法是建立等价流树（最小割树）。

最小割树的一个建立的基础性质：对于 \(G\) 的 \(u,v\) 的最小割 \(F\)，设割去后形成的连通块 \(C_u,C_v\)，取任意 \(u'\in C_u,v'\in C_v\)，均有 \(\lambda(u',v')= \min\{\lambda(u',u),\lambda(v,v'),\lambda(u,v)\}\)。

怎么证明呢？

首先，有一个比较显的三角不等式，\(\lambda(a,b)\ge \min\{\lambda(a,c),\lambda(c,b)\}\)。同样的，\(\lambda(u',v')\ge\min{\lambda(u',u),\lambda(u,v),\lambda(v,v')}\)。

其次，我们取证明大于等于。我们设 \(u,u'\) 的最小割 \(F_u\)，设（全局中）割去后形成的连通块 \(P_u,P_{u'}\)，则由最小割的性质由 \(C_v\subset P_u\) 或者 \(C_v\subset P_{u'}\)。我们分类讨论：若 \(C_v\subset P_u\)，则 \(F_u\) 也同样是 \(u',v'\) 的割集，于是有 \(\lambda(u',v')\le \lambda(u,u')\)；若 \(C_v\subset P_{u'}\)，则 \(F_u\) 也同样是 \(u,v\) 的割集，且 \(F\) 是 \(u',v'\) 的割集，于是又 \(\lambda(u',v')\le \lambda(u,v)\le \lambda(u,u')\)。于是我们就可以证明 \(\lambda(u',v')\le \min(\lambda(u',u),\lambda(u,v),\lambda(v,v'))\)。

递归

有了这个，我们就可以得到一个具体的算法流程。设递归函数 \(\operatorname{EFT}(U)\) 表示求出 \(U\) 这个点集的最小割树，\(E_U\) 表示这个最小割树的边集。

1. 若 \(|U|=1\)，则不需要干任何事情，返回 \((U,\varnothing)\)，然后开摆。否则继续卷。
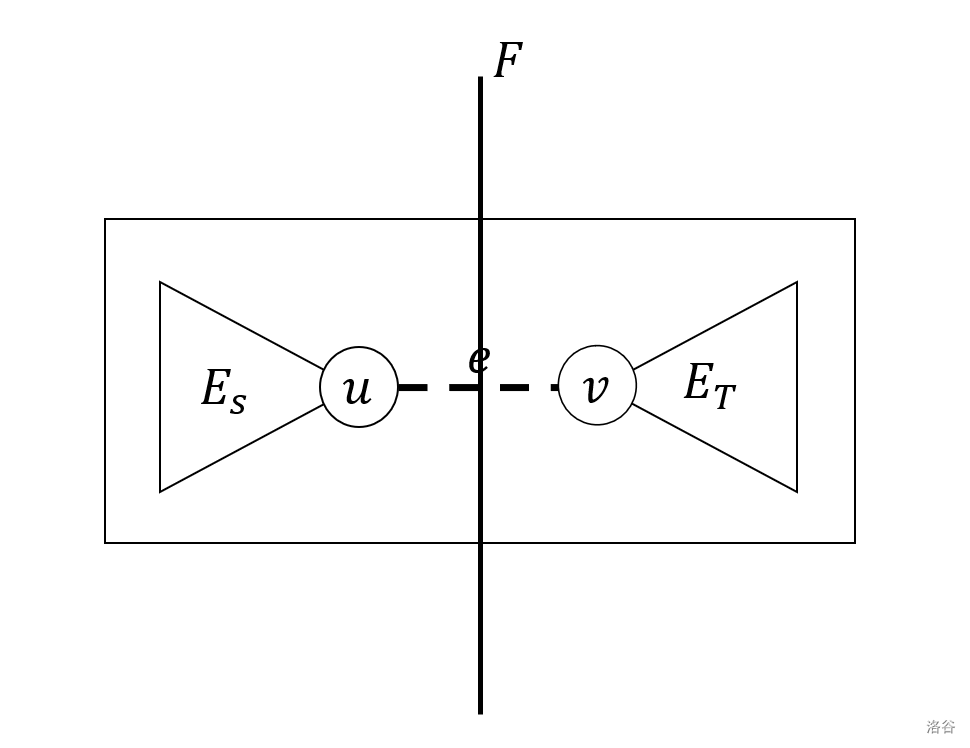
2. 任取两个点 \(u,v\)，求 \(u,v\) 在全图中的最小割 \(F\)，设割去后得到的 \(u,v\) 所在的连通块分别为 \(S^*,T^*\)，然后得到 \(S=S^*\cap U\)，\(T=T^*\cap U\)，通过递归 \(\operatorname{EFT}(S)\) 和 \(\operatorname{EFT}(T)\) 得到 \(E_S\)，\(E_T\)。
3. 新建树边 \(e(u,v)\)，边权为 \(\lambda(u,v)\)，然后返回树 \((U,E_S\cap E_T\cap e)\)，即加入边 \(e\)。

于是我们得到最小割树。可以将 \(u,v\) 的最小 割转化成求树上的最小边权（因为最小割树满足 \(u,v\) 在原图中的最小割等价于 \(u,v\) 的树上路径的最小瓶颈）。

总复杂度 \(O(|V|F)\)。

这是一个非常直观，容易理解的算法。感性理解，是非常对的。如果要理性分析，结合上面的那个基础性质，会发现他更加对了。所以这个算法也非常好记。

迭代

实际上，既然能这样递归做，我们也可以迭代去解决这个问题。迭代时，我们就需要模拟树的一个遍历结构，不能像刚才那样随意加边。

首先我们先钦定一个任意的根节点 \(r\)。同时，我们维护一个点集 \(R\) 表示尚未加入树的结点，\(E_T\) 表示最小割树的边集，\(B_u\) 是动态维护的在上文提到过的 \(C_u\)（并且为了防止加边顺序混乱，对于未遇到过的 \(u\)，\(B_u=\varnothing\)，所以一开始只有 \(B_r=V\setminus r\)）。

我们不断地：

1. 从 \(R\) 中任意去除节点 \(v\)，然后任意找到节点 \(u\) 满足 \(v\in B_u\) 作为准备新加的边 \((u,v)\)。
2. 然后跑一下最大流得到 \(\lambda(u,v)\) 和边割集，设对应的两个连通分量分别为 \(S^*, T^*\)。
3. \(B_v=B_u\cap T^*, B_u=B_u\cap S^*\)。然后加入 \((u,v)\) 这条边，边权为 \(\lambda(u,v)\)。

放上该版本的洛谷上模板题（P4897）代码，常数很大，请忍一下：https://paste.ubuntu.com/p/PtbzBFz7DW/

4 点连通问题

对于 \(k>2\) 的 \(k\) 点连通问题，我们发现这个点连通性是没有传递性的，也就是说我们不能像求边连通问题一样从边连通分量入手去考虑问题。不过同样的，我们还是先看看网络流。

全局点连通度

全局边连通度可以有某种神秘牛逼不需要网络流的算法得到，而点却并非如此。

首先判断两点的局部点连通度可以用 \(O(F)\) 的网络流得到，所以我们仍然可以用 \(O(|V|^2F)\) 的时间去求得全局点连通度。

能不能更优呢？

对于 \(G\) 的全局点割集 \(S\)，如果我们从 \(G\) 中任选 \(\kappa(G)+1\) 个元素，必然会有一个元素不在点割集之中，于是必然存在 \(v\in V\setminus S, u\in V\) 使得 \((u,v)\notin E\) 且 \(\kappa(u,v)=\kappa(G)\)。

于是我们可以有一个算法，通过不断减小维护的 \(\kappa(G)\) 和增大这个 \(V\setminus S\) 的大小，然后找到使得集合大小 \(>\kappa(G)\) 的时候就可以得到真正的点连通度。

具体而言，我们维护一个集合 \(T\)（初始 \(T=V\)） 和数 \(c\) （代表 \(\kappa(G)\)）并且不断地：

1. 判断是否有 \(|T|>c\)。如果有的话就代表结束了。
2. 向 \(T\) 中加入一个新点 \(u\)。
3. 找到所有满足 \(v\notin T\) 满足 \((u,v)\notin E\)，并用网络流算出 \(k=\min_v \kappa(u,v)\)。然后用 \(k\) 去更新这个 \(c\)。

于是复杂度是 \(O(|V|\kappa(G)F)\)。还记得前面说过的界吗？\(\kappa(G)|V|\le 2|E|\)，所以总复杂度 \(O(|E|F)\)。

不难写，但是似乎没题。