梯度下降基础

一 概述

机器学习三大步骤:

• model (define a set of function)
• goodness of function
• pick the "best" function

step1：model

在这里我们建立一个model

这个Model称之为Linear model:

不同的b、w，得到的 f 不尽相同

而我们要找到最能满足要求的一个 f 。

step2 goodness of function

training data：

当我们将准备好的training data（已知10个宝可梦的进化情况），建立一个二维坐标轴。

通过上图可以看出，好像有一个函数能够拟合这些坐标点，而这正是我们想要的，为了选出最契合的 f ，我们要建立一个Loss function L ，也就是函数的函数。

如果我们将 f 的 w 和 b 作为两轴，则在下图中每一点都确定了一个 function f ，而颜色代表output的大小，也就代表该function f 参数的好坏。易理解，smallest点做对应的函数 f 就是我们想要的。

step3 best function

接下来就是选出使Loss function值最小的f。该怎么计算出来呢？可以用线性代数的方法来计算出最佳的w和b。但我们也可以用Gradient Descent方法求出最佳的w和b。

当我们在L(w)的二维平面中时，我们必须要找到函数的最低点。

首先随机选取一个点w0，计算微分也就是斜率，如果为正，则减小w，如果为负，则增大w。

而这有另一个问题，每次要增加或减少多少w值呢，有两个因素影响。第一，即微分值，如果微分值很大或很小，表示此处非常陡峭，那么证明距离最低点还有很远的距离，所以移动的距离就很大。第二个因素是我们事先自己定义的常数项 η 值，即步长(Learning Rate)。

不断重复，经过多次的参数更新后，能达到一个最低点。

 

过程如下：

说到这里大家可能会担心，会不会产生下图左半部分的哪种情况，即不同的起始位置，找到的最低点是不一样的，其实，在我们案例的Linear regression中，是不会出现这种情况的。

最后运行的结果如下图所示

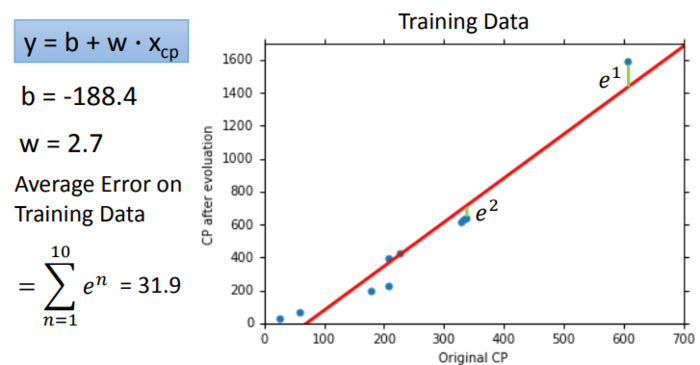
通过上图就会发现，并不是所有的点都能拟合函数，这就会造成很大的预测不准的情况，通过Loss Function也能看出，最优解的值依然很大，在测试数据的表现也不好，所以自然就要想办法做得更好。怎么做得更好呢？这个时候我们可以考虑更换Model。

引入平方

 

引入立方

引入四次方

引入五次方

 

观察以上模型的表现，可以看到随着模型次数的增加，在Training Data上的表现越来越好（前提是Gradient Descent可以找到参数的最优值）。为什么呢？因为复杂的模型包含了简单的模型。

 

 

而在Testing Data上的表现却不一样，甚至在五次方程时，大大超出了我们的预估，那么这种现象就叫做overfitting。

 

所以，function不是越复杂越好，所以我们要选择一个最合适的，由上图可以看出，在三次方程中表现最好。

你是不是以为这样就结束了？答案是否定的。
当我们收集了更多的数据后，将其绘制成图像：

 

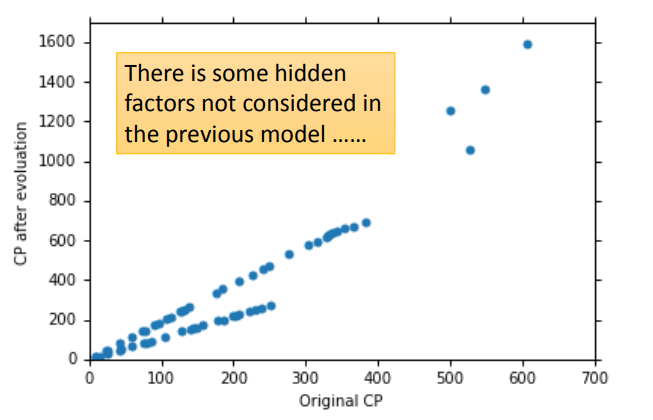
可以看出来，肯定有什么别的因素影响着进化后的CP值。

可以看到，进化后的CP值受物种影响很大。知道了这点后，我们自然要重新设计Model。

 

 

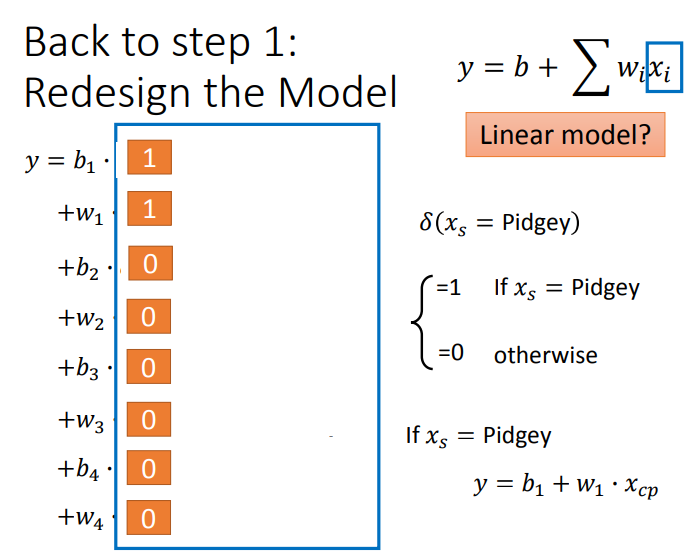
结果如下：

当然还可能有别的特征影响了进化的CP值，比如：

我们还是从重新设置Model，并经过计算得到：

出现了Overfitting的现象，如何改进呢？

 

 

 

二 实例

假设有如下数据：

x_data = [338.,333.,328.,207.,226.,25.,179.,60.,208.,606]
y_data = [640.,633.,619.,393.,428.,27.,193.,66.,226.,1591]

其中，y_data = w * x_data + b，w和b都是参数，让我们用梯度下降（Gradient Descent）的方法将w和b的值找出来。当然，还有许多其他的方法，但我们假装不知道这件事，用Gradient Descent的方法将其找出来。

代码如下：

import numpy as np
import matplotlib.pyplot as plt

x_data = [338.,333.,328.,207.,226.,25.,179.,60.,208.,606]
y_data = [640.,633.,619.,393.,428.,27.,193.,66.,226.,1591]
#ydata=b+w*xdata

x = np.arange(-200,-100,1)# bias
y = np.arange(-5,5,0.1)# weight
z = np.zeros((len(x),len(y)))
X,Y = np.meshgrid(x,y)
for i in range(len(x)):
    for j in range(len(y)):
        b = x[j]
        w = y[j]
        z[j][i]=0
        for n in range(len(x_data)):
            z[j][i] = z[j][i] + (y_data[n] - b - w * x_data[n]) ** 2
        z[j][i] = z[j][i] / len(x_data)

#ydata = b + w * xdata
b = -120 #initial b
w = -4 #initial w
lr = 0.0000001 #learning rata
iteration = 100000

#store initial values for plotting
b_history = [b]
w_history = [w]

#iterations
for i in range(iteration):
    
    b_grad = 0.0
    w_grad = 0.0
    for n in range(len(x_data)):
        b_grad = b_grad - 2.0 * (y_data[n] - b - w * x_data[n]) * 1.0
        w_grad = w_grad - 2.0 * (y_data[n] - b - w * x_data[n]) * x_data[n]
       
        #updata parameters
    b = b - lr * b_grad
    w = w - lr * w_grad
        #store parameters for plotting
    b_history.append(b)
    w_history.append(w)
        
# plot the figure
plt.contourf(x,y,z,50,alpha=0.5,cmap=plt.get_cmap('jet'))
plt.plot([-188.4],[2.67],'x',ms=12,markeredgewidth=3,color='orange')
plt.plot(b_history,w_history,'o-',ms=3,lw=1.5,color='black')
plt.xlim(-200,-100)
plt.ylim(-5,5)
plt.xlabel(r'$b$',fontsize = 16)
plt.ylabel(r'$w$',fontsize = 16)
plt.show()

运行结果如下：

其中，橙色的x代表最优解，图中的黑色块代表了100000次的迭代过程，可以看出此时离最优解还差得远。这显然是Learning Rate不够大，我们不妨把它调大点，比如说lr = 0.000001，也就是增大了10倍，得到结果如下：

离最优解稍微近了一点，不过有一个剧烈震荡的现象。我们不妨再把Learning Rate调大,比如说lr=0.00001，得到结果如下：

糟糕，Learning Rate此时太大了。此时我们该怎么办？如果两个参数都没办法解决，更不用谈更多参数的情况了，只好用大招！——我们要给b和w客制化的Learning Rate。

#ydata = b + w * xdata
b = -120 #initial b
w = -4 #initial w
lr = 1 #learning rata
iteration = 100000

#store initial values for plotting
b_history = [b]
w_history = [w]

lr_b = 0.0 
lr_w = 0.0
#iterations
for i in range(iteration):
    
    b_grad = 0.0
    w_grad = 0.0
    for n in range(len(x_data)):
        b_grad = b_grad - 2.0 * (y_data[n] - b - w * x_data[n]) * 1.0
        w_grad = w_grad - 2.0 * (y_data[n] - b - w * x_data[n]) * x_data[n]
        
    lr_b = lr_b + b_grad ** 2
    lr_w = lr_w + w_grad ** 2
        
        #updata parameters
    b = b - lr / np.sqrt(lr_b) * b_grad
    w = w - lr / np.sqrt(lr_w) * w_grad
        #store parameters for plotting
    b_history.append(b)
    w_history.append(w)
        
# plot the figure
plt.contourf(x,y,z,50,alpha=0.5,cmap=plt.get_cmap('jet'))
plt.plot([-188.4],[2.67],'x',ms=12,markeredgewidth=3,color='orange')
plt.plot(b_history,w_history,'o-',ms=3,lw=1.5,color='black')
plt.xlim(-200,-100)
plt.ylim(-5,5)
plt.xlabel(r'$b$',fontsize = 16)
plt.ylabel(r'$w$',fontsize = 16)
plt.show()

运行结果如下：

可以看到，在100000次的迭代内，找到了最优解。

参考：

https://www.jianshu.com/p/5ac76589ee7b

https://www.jianshu.com/p/8463d08f4379