【数据结构】后缀数组小记

后缀数组小记

目录

• 后缀数组小记
  • 介绍
  • 模板题

简要地介绍了后缀数组相关知识，对原理部分的解析较浅。

介绍

sa[i]: 代表排名 \(i\) 的后缀在原串的下标。

rank[i]: 表示原串下标 \(i\) 所对应的后缀的排名。

height[i]: \(\rm{height}[i] = \rm{LCP}(\rm{suffix(sa[i-1])}, \rm{suffix(sa[i])})\)

\(\rm{LCP(a, b)}\) 代表字符串 \(a,b\) 的最长公共前缀长度。

其中，对于下标为 \(j,k\) 所对应的后缀，不妨设 \(rank[j] < rank[k]\)，我们有：

\[\rm{LCP}(suffix(j), suffix(k)) = min_{rnk=rank[j]+1}^{rank[k]} height[rnk] \]

后缀数组的构建可以通过倍增法，本质上是利用做关键字排序。

例如，对字符串 \(\texttt{aabaaaaab}\) 求排名的过程如下：

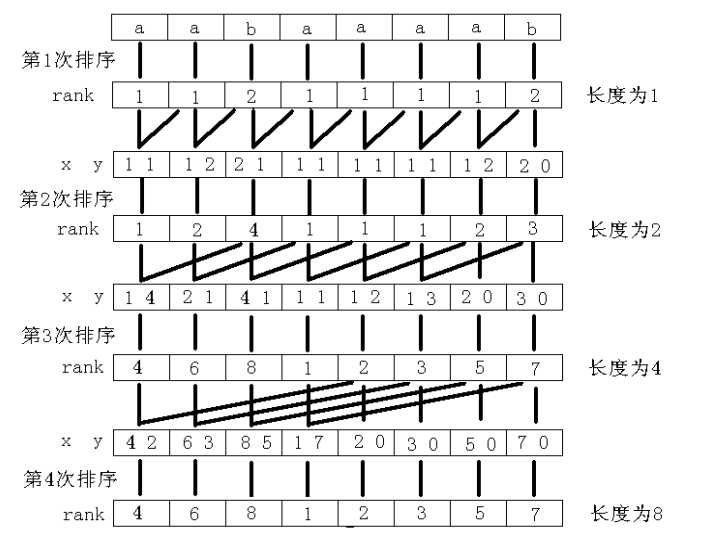
模板题

给定一个长度为 \(n\) 的字符串，只包含大小写英文字母和数字。

将字符串中的 \(n\) 个字符的位置编号按顺序设为 \(1∼n\)。

并将该字符串的 \(n\) 个非空后缀用其起始字符在字符串中的位置编号表示。

现在要对这 \(n\) 个非空后缀进行字典序排序，并给定两个数组 \(SA\) 和 \(Height\)。

特别的，规定 \(Height[1]=0\)。

#include<bits/stdc++.h>
using namespace std;

#define rep(i,a,b) for(int i=(a);i<=(b);i++)
#define dwn(i,a,b) for(int i=(a);i>=(b);i--)

const int N=1e6+5;

int n, m;
char s[N];
int sa[N], x[N], y[N], c[N], rk[N], height[N];

void get_sa(){
	rep(i,1,n) c[x[i]=s[i]]++;
	rep(i,2,m) c[i]+=c[i-1];
	dwn(i,n,1) sa[c[x[i]]--]=i;
	
	for(int k=1; k<=n; k<<=1){
		int num=0;
		rep(i,n-k+1,n) y[++num]=i;
		rep(i,1,n) if(sa[i]>k) y[++num]=sa[i]-k;
		rep(i,1,m) c[i]=0;
		rep(i,1,n) c[x[i]]++;
		rep(i,2,m) c[i]+=c[i-1];
		dwn(i,n,1) sa[c[x[y[i]]]--]=y[i], y[i]=0;
		swap(x, y);
		x[sa[1]]=1, num=1;
		rep(i,2,n) x[sa[i]]=(y[sa[i]]==y[sa[i-1]] && y[sa[i]+k]==y[sa[i-1]+k])? num: ++num;
		if(num==n) break;
		m=num;
	}
}

void get_height(){
	rep(i,1,n) rk[sa[i]]=i;
	for(int i=1, k=0; i<=n; i++){
		if(rk[i]==1) continue;
		if(k) k--;
		int j=sa[rk[i]-1];
		while(i+k<=n && j+k<=n && s[i+k]==s[j+k]) k++;
		height[rk[i]]=k;
	}
}

int main(){
	scanf("%s", s+1);
	n=strlen(s+1), m='z';
	
	get_sa();
	get_height();
	
	rep(i,1,n) cout<<sa[i]<<' '; puts("");
	rep(i,1,n) cout<<height[i]<<' ';
	
	return 0;
}