1. 感性认识“动态规划”
1. 基本概念
是求解决策过程(decision process)最优化的数学方法。把多阶段过程转化为一系列单阶段问题,利用各阶段之间的关系,逐个求解,是一种解决这类过程优化问题的新方法。
2. 使用技巧:
动态规划算法通常用于求解具有某种最优性质的问题!!!特别的 ,动态规划(Dynamic Programming)对于子问题重叠的情况特别有效,因为它将子问题的解保存在表格中,当需要某个子问题的解时,直接取值即可,从而避免重复计算!
3. 基本思想与策略
我们通过一个问题来引出:
提问:动态规划与分治法有什么不同?
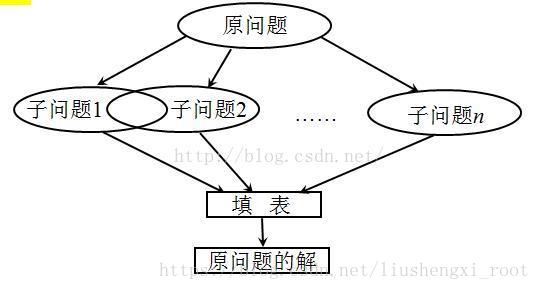
答:适合于用动态规划求解的问题,经分解得到子问题往往不是互相独立的。若用分治法来解这类问题,则分解得到的子问题数目太多,有些子问题被重复计算了很多次。如果我们能够保存已解决的子问题的答案,而在需要时再找出已求得的答案,这样就可以避免大量的重复计算,节省时间。我们可以用一个表来记录所有已解的子问题的答案。不管该子问题以后是否被用到,只要它被计算过,就将其结果填入表中。这就是动态规划法的基本思路。具体的动态规划算法多种多样,但它们具有相同的填表格式。
说明:具体的填表情况还是要看具体所涉及的情景,有时可能不需要保存全部的子状态,而只需要保存之前的1~2个状态即可。 比如:爬楼梯问题等
4. 适用的情况
1)两个必备要素
适合应用动态规划方法求解的最优化问题应该具备两个重要的要素:最优子结构和子问题重叠。
(a)最优子结构:问题的最优解由相关子问题的最优解组合而成,并且可以独立求解子问题!
(b)子问题重叠:递归过程反复的在求解相同的子问题。
2)三个性质
能采用动态规划求解的问题的一般要具有3个性质:
(a) 最优化原理:如果问题的最优解所包含的子问题的解也是最优的,就称该问题具有最优子结构,即满足最优化原理。
(b) 无后效性:即某阶段状态(定义的新子问题)一旦确定,就不受这个状态以后决策的影响。也就是说,某状态以后的过程不会影响以前的状态,只与其以前的状态有关。
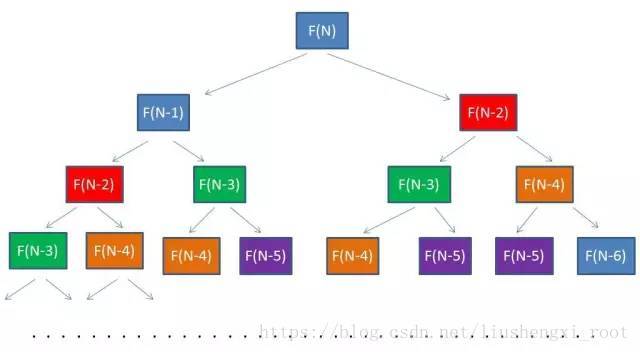
(c)有重叠子问题:即子问题之间是不独立的(分治法是独立的),一个子问题在下一阶段决策中可能被多次使用到。(该性质并不是动态规划适用的必要条件,但是如果没有这条性质,动态规划算法同其他算法相比就不具备优势)
比如下面的问题:相同颜色的子问题就被重复用到。
5. 求解的基本步骤
实际应用中可以按以下几个简化的步骤进行设计:
(1)分析最优解的性质,并刻画其结构特征,这一步的开始时一定要从子问题入手。
(2)定义最优解变量,定义递归最优解公式。
(3)以自底向上计算出最优值(或自顶向下的记忆化方式(即备忘录法))
(4)根据计算最优值时得到的信息,构造问题的最优解
2.实战
零钱兑换
给定不同面额的硬币 coins 和一个总金额 amount。
编写一个函数来计算可以凑成总金额所需的最少的硬币个数。
如果没有任何一种硬币组合能组成总金额,返回 -1。
示例 1:
输入: coins = [1, 2, 5], amount = 11
输出: 3
解释: 11 = 5 + 5 + 1
示例 2:
输入: coins = [2], amount = 3
输出: -1
说明:
你可以认为每种硬币的数量是无限的。思路: 首先我们根据以上所说的去思考。假如 amount == 11 ,那么它之前的状态可能就是 10,9,6 ,怎么来的呐?很显然就是11-1,11-2,11-5,要让11找的硬币数量最少,那么就是(10,9,6)找的硬币数量最少的那一个,之后继续按照这种思路进行思考。考虑到子问题重叠的情况,我们在实现的过程中对其进行填表。
如何实现:
用待找零的数值k描述子结构/状态,记作MinCoinCount[k],其值为所需的最小硬币数。对于不同的硬币面值coins[0…n],有 MinCoinCount[k] = min(MinCoinCount[k-coin[0]] , MinCoinCountk-coin[1]], …)+1。对应于给定数目的找零amount,需要求解MinCoinCount[amount]的值。
通过源代码:
#include<iostream>
#include<vector>
#include<limits.h>
using namespace std;
class Solution {
public:
int coinChange(vector<int>& coins, int amount) {
vector<int> MinCoinCount(amount+1, INT_MAX-1) ;
MinCoinCount[0] = 0 ;
//MinCoinCount[k],(k为零钱数) MinCoinCount[k] 为所需的最小硬币数量
for (int i = 1 ; i <= amount ; ++i)
{
for (int j = 0; j < coins.size() ; ++j )
{
if ( i - coins[j] >= 0 &&
MinCoinCount[i - coins[j]]+1 < MinCoinCount[i])
MinCoinCount[i] = MinCoinCount[i - coins[j]] + 1 ;
}
}
if (MinCoinCount[amount] == INT_MAX-1 )
return -1 ;
else
return MinCoinCount[amount];
}
};参考文章:
https://blog.csdn.net/roslei/article/details/60867423
建议没事干的时候把这东西看看:^_^
https://www.sohu.com/a/153858619_466939