在刷华为机试的在线编程,碰到一个类似01背包问题的题目,综合了一些资料,写一些自己的理解
01背包问题就是在有限的称重容量下,求最大价值的问题
假设几个参数:
w[i]:第i个物品的重量;
p[i]:第i个物品的价值;
v[i][j]:表示在前i个物品中,总重量为j时的最大价值;
v[i-1][j-w[i]]:表示前i-1个物品中,加入第i个物品后的承重容量下的最大价值;
我们分析:在加入第i件物品前,我们要考虑要不要加进去,不加进去,那么就是v[i][j]=v[i-1][j];如果加进去,那么v[i][j]=v[i-1][j-w[i]]+p[i]
具体的例子例如
有编号分别为a,b,c,d,e的五件物品,它们的重量分别是2,2,6,5,4,它们的价值分别是6,3,5,4,6,现在给你个承重为10的背包,如何让背包里装入的物品具有最大的价值总和?
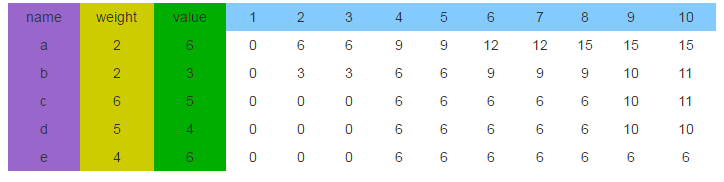
首先要明确这张表是至底向上,从左到右生成的。
为了叙述方便,用e2单元格表示e行2列的单元格,这个单元格的意义是用来表示只有物品e时,有个承重为2的背包,那么这个背包的最大价值是0,因为e物品的重量是4,背包装不了。
对于d2单元格,表示只有物品e,d时,承重为2的背包,所能装入的最大价值,仍然是0,因为物品e,d都不是这个背包能装的。
同理,c2=0,b2=3,a2=6。
那么状态转移方程就可以表示为:
v[i][j]=max{v[i-1][j],v[i-1][j-w[i]]+p[i]}
那么代码实现如下:
import java.util.*;
public class Main {
public static void main(String[] args) {
// TODO Auto-generated method stub
int weight = 10;
int n = 3;
int[] w = {3,4,5};
int[] p = {4,5,6};
System.out.println(getMaxweight(w, p, weight, n));
}
public static int getMaxweight(int[] w, int[] p, int weight, int n){
int[][] value = new int[n+1][weight+1];
for(int i = 1;i<=n;i++){
for(int j = 1;j<=weight;j++){
//当物品为i件重量为j时,如果第i件的重量(w[i-1])小于重量j时,c[i][j]为下列两种情况之一:
//(1)物品i不放入背包中,所以c[i][j]为c[i-1][j]的值
//(2)物品i放入背包中,则背包剩余重量为j-w[i-1],所以c[i][j]为c[i-1][j-w[i-1]]的值加上当前物品i的价值
if(w[i-1]<=j){
value[i][j]=Math.max(value[i-1][j], value[i-1][j-w[i-1]]+p[i-1]);
}
}
}
return value[n][weight];
}
}