一、队列是什么?
队列queue:一种线性数据结构,队列中的元素只能先入先出(First In First Out,简称FIFO),队列的出口端叫作队头(front),队列的入口端叫作队尾(rear)。
队列这种数据结构本身是有序列表,既可以用数组来实现,也可以用链表来实现:
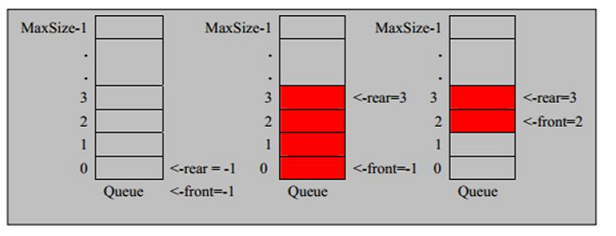
如图:数组实现队列,队尾往往设置在最后一个元素的下一个位置。

队列的操作一般分为-------------入队和出队
---入队:把新元素放入队列中,只允许在队尾的位置放入元素,新元素的下一个位置将会成为新的队尾。
---出队:把元素移出队列,只允许在队头一侧移出元素,出队元素的后一个元素将会成为新的队头。
二、单向队列怎么实现?
思路分析:入队和出队
入队:a. 当 front == rear【空】,将尾指针往后移:rear+1。
b. 指针 rear 小于队列的最大下标 maxSize-1,则将数据存入 rear 所指的数组元素中,否则无法存入数据。rear==maxSize-1[队列满]
//定义队列的基本组成
private int maxSize; //表示数组的最大容量
private int front; //队头指针
private int rear; //队尾指针
private int[] arr;
//创建队列构造器
public ArrayQueue(int arrMaxSize) {
this.maxSize = arrMaxSize;
this.front = -1; //指向队列头部的之前的位置,没有任何数据时,指向虚无
this.rear = -1; //指向队列尾部的位置,最后一个元素的位置
this.arr = new int[this.maxSize];
}
//判断队列是否满了
public boolean isFull() {
//(rear+1)%array.length == front)
return rear == maxSize;
}
//判断队列是否为空
public boolean isEmpty() {
return rear == front;
}
//添加数据到队列
public void addQueue(int element) {
if(isFull()) {
System.out.println("队列已满");
return ;
}
rear++;
arr[rear] = element;
}
//获取队列值,出队列
public int getQueue() {
//判断是否为空
if(isEmpty()) {
throw new RuntimeException("队列为空");
}
front++;
int value = arr[front];
return value;
}
//显示队列的所有数据
public void showQueue() {
//遍历
if(isEmpty()) {
System.out.println("队列为空,遍历个锤子");
}
for(int i=0; i < arr.length; i++) {
System.out.printf("arr[%d]=%d
",i,arr[i]);
}
}
//实现队列头部
public int headQueue() {
if(isEmpty()) {
System.out.println("队列为空,没有头");
}
return arr[front+1];
}
缺陷:数组无法复用,造成空间浪费。
三、环形队列怎么实现?

//注意环形队列最大实际有效值为 最大值-1,因为需要空余一个数组位,用于作变动,让数组尾指针重新指回数组的首位(取模之法)
//定义队列的基本机构
private int maxSize; //表示数组的最大容量
private int front; //队头指针,队列的第一个元素,初始值为0
private int rear; //队尾指针,队列最后一个元素的后一个位置,初始值为0
private int[] arr;
//创建队列构造器
public CirQueue(int arrMaxSize) {
this.maxSize = arrMaxSize;
this.arr = new int[this.maxSize];
}
//判断队列是否满了
public boolean isFull() {
//(rear+1)%array.length == front)
return (rear+1)%maxSize == front;
}
//判断队列是否为空
public boolean isEmpty() {
return rear == front;
}
//添加数据到队列
public void addQueue(int element) {
if(isFull()) {
System.out.println("队列已满");
return ;
}
//将元素加入队列
arr[rear] = element;
//rear 后移,这里必须考虑取模---把尾指针定位到数组开始位置,循环利用数组
rear = (rear + 1) % maxSize;
}
//获取队列值,出队列
public int getQueue() {
//判断是否为空
if(isEmpty()) {
throw new RuntimeException("队列为空");
}
//这里需要分析出front是指向队列的第一个元素
//1.先把front对应的值保留到一个临时变量
//2.将front后移-----考虑取模
//3.将临时保存的变量返回
int value = arr[front];
front=(front+1)%maxSize;
return value;
}
//显示队列的所有数据
public void showQueue() {
//遍历
if(isEmpty()) {
System.out.println("队列为空,遍历个锤子");
return;
}
//输出---队列---遍历
//从哪里开始遍历,到哪里结束呢?----头指针在哪,就从那个开始
//得到环形数组中具有多少个元素。-----当前队列的有效元素具体--(rear + maxSize - front) % maxSize
//从头指针 开始
for(int i=front; i < front+size(); i++) {
System.out.printf("arr[%d]=%d ",i % maxSize,arr[i % maxSize ]);
}
}
//求出当前队列有效数据的个数
public int size() {
return (rear + maxSize - front) % maxSize;
}
//实现队列头部
public int headQueue() {
if(isEmpty()) {
System.out.println("队列为空,没有头");
}
return arr[front+1];
}
方法二:
private int[] array;
private int front;
private int rear;
//环形队列构造器
public MyQueue(int capacity){
this.array = new int[capacity];
}
//入队
public void enQueue(int element) throws Exception {
if((rear+1)%array.length == front){
throw new Exception(" 队列已满!");
}
array[rear] = element;
rear =(rear+1)%array.length; }
//出队
public int deQueue() throws Exception {
if(rear == front){
throw new Exception(" 队列已空!");
}
int deQueueElement = array[front];
front =(front+1)%array.length;
return deQueueElement;
}
//输出---队列---遍历
public void output(){
for(int i=front; i!=rear; i=(i+1)%array.length){
System.out.println(array[i]);
}
}
//此法来源于---漫画算法:小灰的算法之旅