20172319 2018.10.10-10.18
《程序设计与数据结构》第5周学习总结
目录
教材学习内容总结
第九章 排序和查找:
- 9.1 查找:
- 查找(Searching) : 确定目标元素是否存在于项目组中。
- 查找池(Search pool) : 进行查找的项目组。
- 高效地完成查找是我们所需要追求的目标;因此,在算法上尽可能地减少比较这一操作的次数。
- 9.1.1 静态方法:
- 静态方法(Static method) : 又称类方法(Class method),可以通过类名来激活,无需为了调用一个静态方法而去实例化该类的一个对象。
- 静态方法不能引用实例变量,因为其并非作用于具体的对象中;但其可以引用静态变量,因为其存在与具体的对象无关。
- 9.1.2 泛型方法:
- 创建泛型方法的方法:在方法头的返回类型前插入一个泛型声明即可,泛型声明必须位于返回类型之前,这样泛型才能作为返回类型的一部分。
public static <T extends Comparable<T>> boolean
linearSearch(T[] data, int min, int max, T target)

-
**9.1.3 线性查找法 ** -
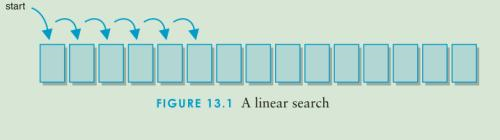
线性查找,又称其为顺序查找,是一种最简单的查找方法,其基本思想:从查找池的第一个记录开始,逐个比较记录的关键字,直到和给定的关键字相等,则查找成功;若比较结果与查找池中n个记录的关键字都不等,则查找失败。
-
**时间复杂度为 ** : O(n);
-
**平均查找长度 ** :ASL = (n + ······ + 2 + 1)/ n = (n + 1 ) / 2
-
优缺点:
-
- **优点: ** 算法简单,适应面广,对表的结构无任何要求,无论记录是否按关键字有序均可应用。
-
- **缺点: ** ASL较大,当n较大时,查找效率低。
- **缺点: ** ASL较大,当n较大时,查找效率低。
-
代码实现:
public static <T> boolean linearSearch(T[] data, int min, int max, T target)
{
int index = min;
boolean found = false;
while (!found && index <= max)
{
found = data[index].equals(target);
index++;
}
return found;
}
-
**9.1.4 二分查找法 ** -
**二分查找 **:也称折半查找,效率较高,但要求线性表必须采用顺序存储结构,且表中元素按关键字有序排列。
-
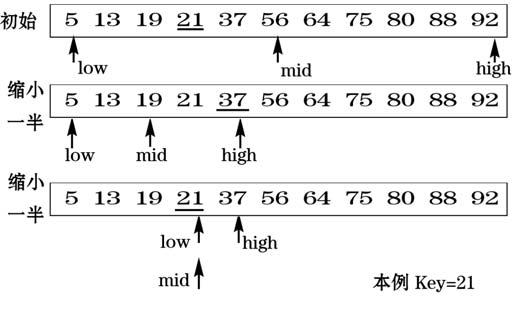
**基本原理 ** : 首先先确定在该存储结构的中点位置;之后将待查找的值与中值进行比较;若二者相等,则查找成功并返回此位置,否则确定新的查找区间,再继续进行二分查找:
-
- 1.若待查找值大于中值,则新的查找区间为前一查找区间的中值及区间后半部分元素。
-
- 2.若待查找值小于中值,则新的查找区间为前一查找区间的中值及区间前半部分元素。
-
从初始的查找区间开始,每经过一次与当前查找区间的中点位置上的结点值的比较,即可判断查找是否成功,不成功则当前的查找区间便缩小一半。这一过程一直重复,直至找到待查找值的位置,或者直至当前的查找区间为空(即查找失败)为止。
-
**时间复杂度 ** :O(log₂n);
-
- | 第n次查询 | 剩余待查询元素的数量 |
| -------- | :----------------: |
| 1 | N/2 |
| 2 | N/(2^2) |
| 3 | N/(2^3) |
| 4 | N/(2^4) |
| 5 | N/(2^5) |
| 6 | N/(2^6) |
| ······ | ······ |
| ······ | ······ |
| K |N/(2^K) |
- | 第n次查询 | 剩余待查询元素的数量 |
-
无论如何,只要还在查找的过程中,N/(2^K)>=1,而我们所考虑的**最坏情况 ** 无非是N/(2^K)=1,所以有K = log₂n。
-
平均查找长度: ASL = log₂(n+1)-1。(现有知识储备不足,无法做出相应推导)
-
优缺点:
-
- **优点: ** 查找的效率较高。
-
- 缺点: ** 只适用于有序表,且限于顺序存储结构,对线性链表无法有效的进行查找,在一些特殊情况 **下查找效率很低:所查找的元素是表中的第一个元素和最后一个元素。
- 缺点: ** 只适用于有序表,且限于顺序存储结构,对线性链表无法有效的进行查找,在一些特殊情况 **下查找效率很低:所查找的元素是表中的第一个元素和最后一个元素。
-
代码实现:
public static <T extends Comparable<T>> boolean binarySearch(T[] data, int min, int max, T target)
{
boolean found = false;
int midpoint = (min + max) / 2; // determine the midpoint
if (data[midpoint].compareTo(target) == 0) {
found = true;
} else if (data[midpoint].compareTo(target) > 0)
{
if (min <= midpoint - 1) {
found = binarySearch(data, min, midpoint - 1, target);
}
}
else if (midpoint + 1 <= max) {
found = binarySearch(data, midpoint + 1, max, target);
}
return found;
}
-
**9.2 排序 ** -
**排序(Sorting): ** 基于某一标准,以升序或降序的形式将项目池中的元素按某个规定好的序列进行排列。
-
9.2.1 选择排序法:
-
**选择排序(Selection Sort): ** 在要排序的一组数中,选出最小的一个数与第一个位置的数交换;然后在剩下的数当中再找最小的与第二个位置的数交换,如此循环到倒数第二个数和最后一个数比较为止。

-
代码实现:
public static <T extends Comparable<T>> void selectionSort(T[] data)
{
long startTime=System.nanoTime(); //获取开始时间
int Total_number_of_comparisons = 0;
int min;
T temp;
for (int index = 0; index < data.length-1; index++)
{
min = index;
for (int scan = index+1; scan < data.length; scan++) {
Total_number_of_comparisons++;
if (data[scan].compareTo(data[min])<0) {
min = scan;
}
}
swap(data, min, index);
}
long endTime=System.nanoTime(); //获取结束时间
System.out.println("程序运行时间: "+(endTime-startTime)+"ns");
System.out.println("总比较次数: " + Total_number_of_comparisons);
}
-
外层循环: 控制下一个最小值在数组中的存储位置。
-
内层循环: 扫描所有大于或等于外层循环指定索引的位置来找出剩余列表的最小值。
-
在确定最小值后,将其和存储在索引位置处的值交换。
-
9.2.2 插入排序法:
-
**插入排序(Insertion Sort): ** 每步将一个待排序的记录,按其顺序码大小插入到前面已经排序的字序列的合适位置(从后向前找到合适位置后),直到全部插入排序完为止。

-
代码实现:
public static <T extends Comparable<T>> void insertionSort(T[] data)
{
long startTime=System.nanoTime(); //获取开始时间
int Total_number_of_comparisons = 0;
for (int index = 1; index < data.length; index++)
{
T key = data[index];
int position = index;
// shift larger values to the right
while (position > 0 && data[position-1].compareTo(key) > 0)
{
data[position] = data[position-1];
position--;
Total_number_of_comparisons++;
}
data[position] = key;
}
long endTime=System.nanoTime(); //获取结束时间
System.out.println("程序运行时间: "+(endTime-startTime)+"ns");
System.out.println("总比较次数: " + Total_number_of_comparisons);
}
-
外层循环: 控制下一个插入值在数组中的索引。
-
内层循环: 将当前的插入值和存储在更小的索引处的值进行比较。
-
若当前插入值小于position的值,则将该值移位至右边。
-
9.2.3 冒泡排序法:
-
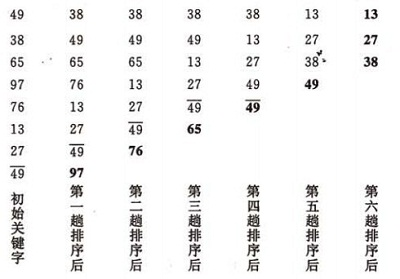
**冒泡排序(Bubble Sort): ** 重复地走访过要排序的数列,一次比较两个元素,如果他们的顺序错误就把他们交换过来。走访数列的工作是重复地进行直到没有再需要交换,也就是说该数列已经排序完成,越小的元素会经由交换慢慢“浮”到数列的顶端。
-
代码实现:
-
- 数组形式:
public static <T extends Comparable<T>> void bubbleSort(T[] data)
{
long startTime=System.nanoTime(); //获取开始时间
int Total_number_of_comparisons = 0;
int position, scan;
T temp;
for (position = data.length - 1; position >= 0; position--)
{
for (scan = 0; scan <= position - 1; scan++)
{
if (data[scan].compareTo(data[scan+1]) > 0) {
swap(data, scan, scan + 1);
}
Total_number_of_comparisons++;
}
}
long endTime=System.nanoTime(); //获取结束时间
System.out.println("程序运行时间: "+(endTime-startTime)+"ns");
System.out.println("总比较次数: " + Total_number_of_comparisons);
}
- 外层循环: 对数据进行n-1轮遍历
- 内层循环: 从头至尾扫描数据,对相邻数据进行成对比较,若符合条件则进行交换。
-
- 链表形式(Exp1):
public void Bubble_sort(Linked_list_node Head,Linked_list linked_list){
Linked_list_node temp = null, tail = null;
temp = head;
int count=1;
while(temp.next != tail){
while(temp.next != tail){
if(temp.number > temp.next.number){
int temp_number = temp.number;
temp.number = temp.next.number;
temp.next.number = temp_number;
System.out.print("The list sorted by the "+ count + " truly bubbling sort is : ");
System.out.println(linked_list);
System.out.print("The number of linked elements is : " + linked_list.getCount() + "
" );
count++;
}
temp = temp.next;
}
tail = temp;
temp = head;
}
}
-
9.2.4 快速排序法:
-
快速排序(Quick Sort): 通过一趟排序将待排序记录分割成独立的两部分,其中一部分记录的关键字均比另一部分关键字小,则分别对这两部分继续进行排序,直到整个序列有序。


-
代码实现:
private static <T extends Comparable<T>>
int partition(T[] data, int min, int max)
{
T partitionelement;
int left, right;
int middle = (min + max) / 2;
// use the middle data value as the partition element
partitionelement = data[middle];
// move it out of the way for now
swap(data, middle, min);
left = min;
right = max;
while (left < right)
{
// search for an element that is > the partition element
while (left < right && data[left].compareTo(partitionelement) <= 0) {
left++;
}
// search for an element that is < the partition element
while (data[right].compareTo(partitionelement) > 0) {
right--;
}
// swap the elements
if (left < right) {
swap(data, left, right);
}
}
// move the partition element into place
swap(data, min, right);
return right;
}
- 先调用partition方法(返回分区元素值的索引)来将排序区域分割成两个分区。
- 然后两次递归调用quicksort方法来对两个分区元素进行排序。
private static <T extends Comparable<T>> void quickSort(T[] data, int min, int max)
{
if (min < max)
{
// create partitions
int indexofpartition = partition(data, min, max);
// sort the left partition (lower values)
quickSort(data, min, indexofpartition - 1);
// sort the right partition (higher values)
quickSort(data, indexofpartition + 1, max);
}
}
-
9.2.5 归并排序法:
-
归并排序(Merge Sort): 将两个(或两个以上)有序表合并成一个新的有序表,即把待排序序列分为若干个子序列,每个子序列是有序的。然后再把有序子序列合并为整体有序序列。


-
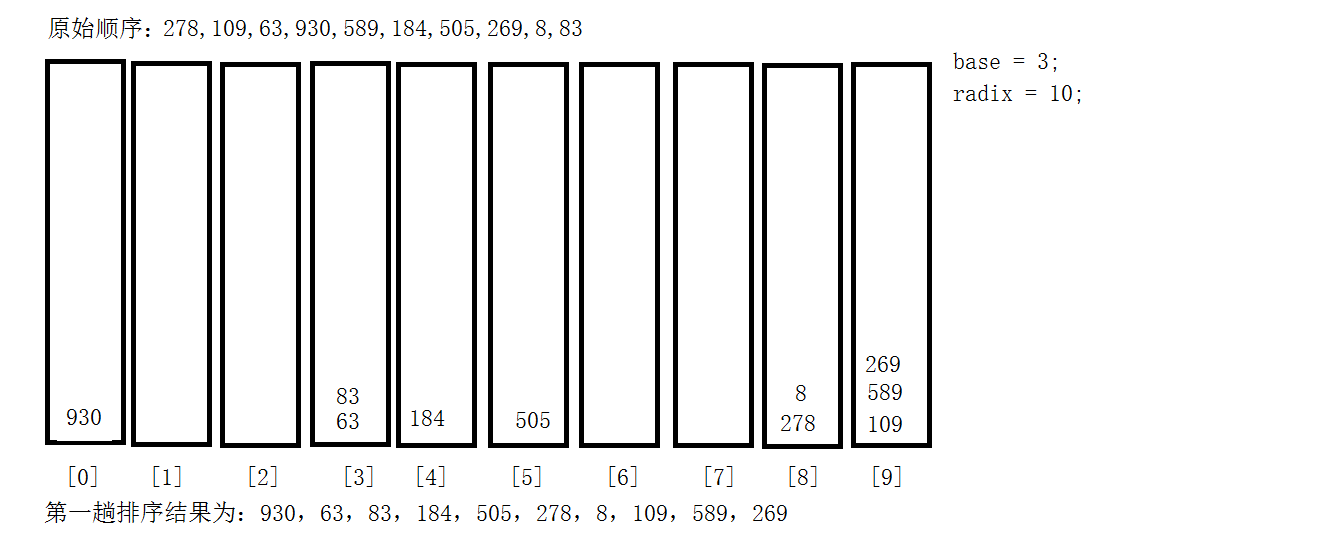
9.3 基数排序法

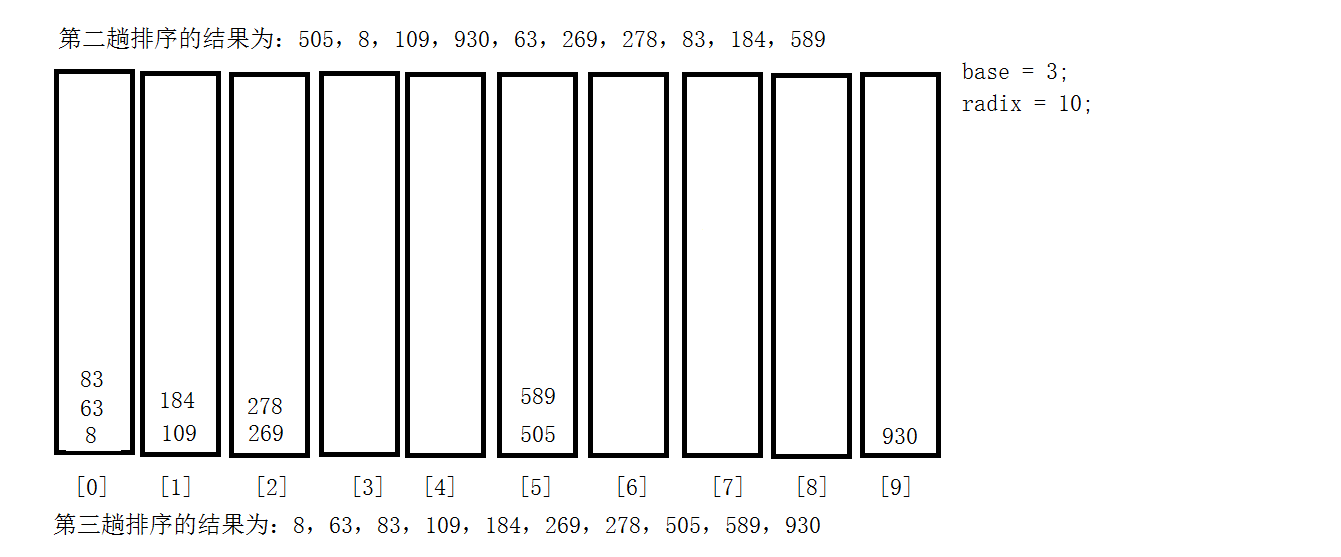
教材学习中的问题和解决过程
- 问题1:在二分查找中,若查找的项目组里元素个数是偶数个,中间项如何确定?
- 解决:
- 解释1:对于查找条件为等式的情况,mid指针可以指向中间偏左,也可以指向中间偏右,对于查找条件为不等式时,要根据具体情况选择,查找大于某数的第一个数值时选择指向中间偏左,查找小于某数的第一个数值时选择之下是那个中间偏右。
- 解释2:二分查找一般都是左除右加1,意思是如果现在你的查找区间是(k,m),那么中间点 mid = (k + m) / 2;如果你查找的节点在左边就查找 (k, mid),在右边就查找(mid+1,m)。
- 解释3:一般来说向下取整,比如8个数:1,2,3,4,5,6,7,8,mid=(1+8)/2=4 。
代码调试中的问题和解决过程
-
问题1:PP9.2的题意吃得不是很透彻。
-
解决:
-
间隔排序法是冒泡排序法的一种变异,则其大体上的代码结构不会发生变化
-
仿照冒泡排序法,我的初始代码是这样的,这里间隔为2:
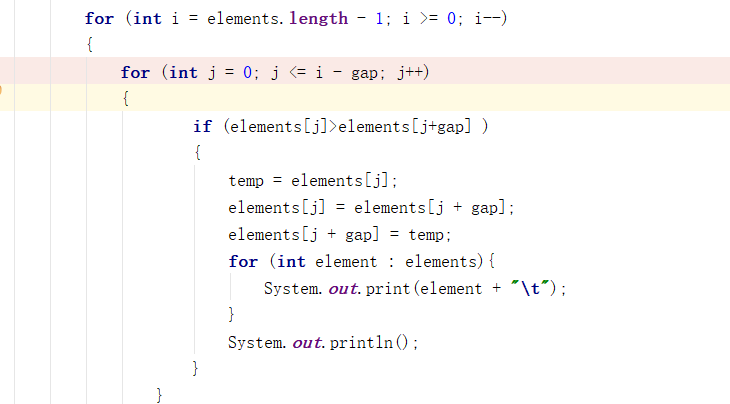
- 运行结果如下:
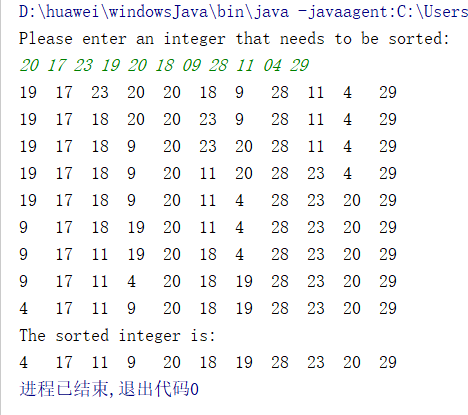
- 可以看到,经过遍历比较后,相应间隔的元素都发生了对应的置换,而彼此相邻的元素却没有经过比较,因此导致排序并不完整;
- 而要想相邻的元素也参与到比较之中,那之后的遍历所取的间隔就要相应地发生一定的变化;
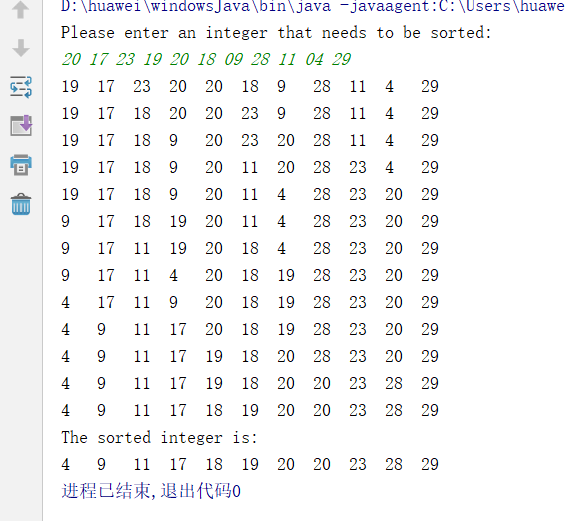
- 作出相应更改之后的代码:
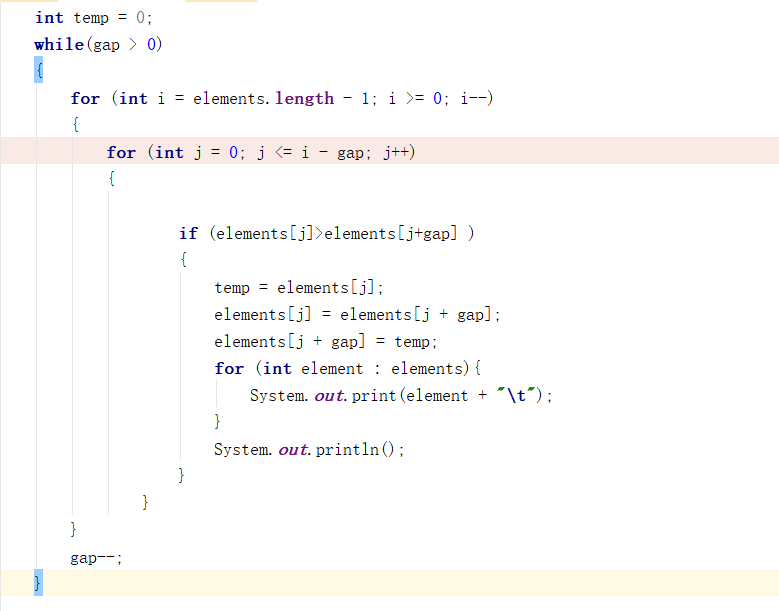
- 相应的运行结果:
代码托管

上周考试错题总结
-
错题1:无任何错题。
-
解决:
-
错题2:
-
解决:
-
错题3:
-
解决:
结对及互评
点评过的同学博客和代码
- 本周结对学习情况:
- 20172316赵乾宸
- 博客中值得学习的或存在问题:
- 20172329王文彬
- **博客中值得学习的或存在问题: **
- 博客内容充实、排版整齐、对教材内容有经过一番认真思考、继续保持。
- 代码截图做标注时应尽量避免遮挡代码。
- Markdown的部分缩进有误。
- 教材问题2提出得很好,可以看出近断时间来反复使用链表、数组去实现同一类型的数据结构起得了一定的成效。
学习进度条
| 代码行数(新增/累积) | 博客量(新增/累积) | 学习时间(新增/累积) | |
|---|---|---|---|
| 目标 | 3000行 | 15篇 | 300小时 |
| 第一周 | 0/0 | 1/1 | 12/12 |
| 第二周 | 935/935 | 1/2 | 24/36 |
| 第三周 | 849/1784 | 1/3 | 34/70 |
| 第四周 | 3600/5384 | 1/5 | 50/120 |
| 第五周 | 2254/7638 | 1/7 | 50/170 |