题目描述
沙都子有一个序列,第i 个位置的数为ai。她知道,该序列共有2n − 1 个子序
列,但有一些子序列长得一样。于是她提出了一个问题:该序列的本质不同的
子序列有多少种呢?
对于1 ≤ p1 < p2 < · · · < pm ≤ n(m 是任意正整数),称(ap1 , ap2 , . . . , apm) 是
一个子序列。
两个子序列(ap1 , . . . , apl ) 和(aq1 , . . . , aqm) 本质相同,当且仅当l = m,且对所
有i = 1, . . . ,m 都满足api = aqi。
列,但有一些子序列长得一样。于是她提出了一个问题:该序列的本质不同的
子序列有多少种呢?
对于1 ≤ p1 < p2 < · · · < pm ≤ n(m 是任意正整数),称(ap1 , ap2 , . . . , apm) 是
一个子序列。
两个子序列(ap1 , . . . , apl ) 和(aq1 , . . . , aqm) 本质相同,当且仅当l = m,且对所
有i = 1, . . . ,m 都满足api = aqi。
输入
第一行,一个整数n。
第二行,n 个非负整数ai。
第二行,n 个非负整数ai。
输出
答案模10^9 + 7。
数据范围限制
对于25% 的数据,1 ≤ n ≤ 10。
对于50% 的数据,1 ≤ n ≤ 10^3。
对于100% 的数据,1 ≤ n ≤ 10^6,0 ≤ ai ≤ 10^6。
对于50% 的数据,1 ≤ n ≤ 10^3。
对于100% 的数据,1 ≤ n ≤ 10^6,0 ≤ ai ≤ 10^6。
Solution:
这道题更像是一道基础的模型题目,题意十分简单,不难看出是一道统计类型的Dp
我们可以发现,对于以某一个Ai为结尾可构成的本质不同子序列当中,其实无非就两种情况,一个是自己单独成为一个子序列,另一个就是与之前已经形成的子序列连接起来构成新的子序列。
于是我们很容易得到一个基础的方程式:
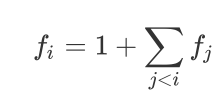
但是如何保证本质不同呢?其实只要在每次方程减去所有同样以Ai结尾的f就好了
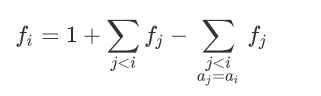
然后我们可以通过维护前缀和的方式来解决两个求和函数,将复杂度降低至O(N)
Code:
1 #include<bits/stdc++.h>
2 const int P=1e9+7;
3 using namespace std;
4 int Dp[1000132],A[1000123],Sum[1000123],Gp[1000123],N;
5 int main()
6 {
7 scanf("%d",&N);
8 for(int i=1;i<=N;i++)
9 scanf("%d",&A[i]);
10 for(int i=1;i<=N;i++){
11 Dp[i]=(1+Sum[i-1]-Gp[A[i]])%P;
12 Sum[i]=(Sum[i-1]+Dp[i])%P;
13 Gp[A[i]]=(Gp[A[i]]+Dp[i])%P;
14 }
15 printf("%d",Sum[N]);
16 return 0;
17 }
