一、核心思想
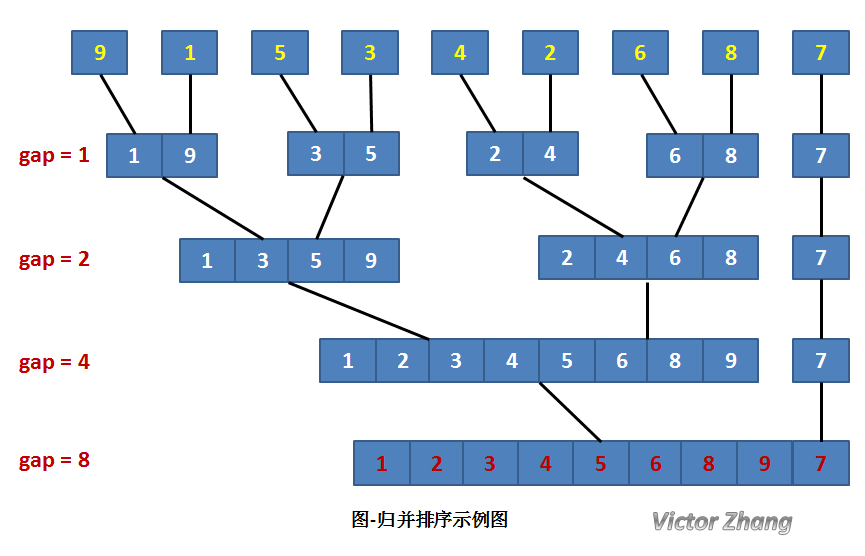
将待排序序列R[0...n-1]看成是n个长度为1的有序序列,将相邻的有序表成对归并,得到n/2个长度为2的有序表;将这些有序序列再次归并,得到n/4个长度为4的有序序列;如此反复进行下去,最后得到一个长度为n的有序序列。
综上可知:
归并排序其实要做两件事:
(1)“分解”——将序列每次折半划分。
(2)“合并”——将划分后的序列段两两合并后排序。
我们先来考虑第二步,如何合并?
在每次合并过程中,都是对两个有序的序列段进行合并,然后排序。
这两个有序序列段分别为 R[low, mid] 和 R[mid+1, high]。
先将他们合并到一个局部的暂存数组R2中,带合并完成后再将R2复制回R中。
为了方便描述,我们称 R[low, mid] 第一段,R[mid+1, high] 为第二段。
每次从两个段中取出一个记录进行关键字的比较,将较小者放入R2中。最后将各段中余下的部分直接复制到R2中。
经过这样的过程,R2已经是一个有序的序列,再将其复制回R中,一次合并排序就完成了。
二、核心代码

public static void main(String[] args) { Random ran=new Random(); int a[]=new int[10]; System.out.println("排序前"); //生成一个随机数组 for(int i=0;i<a.length;i++){ a[i]=ran.nextInt(100); System.out.print(a[i]+" "); } System.out.println(); //调用排序方法 sort(a,0,a.length-1); System.out.print("排序后"); //输出排序后结果 for (int i = 0; i < a.length; i++) { System.out.print(a[i]+" "); } } //分割数组 private static void sort(int[] a, int low, int hight) { //将数组以mid分成左右两部分,直到分到不能再分 int mid=(low+hight)/2; //判断是否还可以继续分割 if(low<hight){ //递归分割左半部分 sort(a,low,mid); //递归分割右半部分 sort(a,mid+1,hight); //排序并将分割的数组组合成新的有序序列 Merge(a,low,hight,mid); } } private static void Merge(int[] a, int low, int hight, int mid) { int[] b=new int[hight-low+1];//新建临时数组存储有序序列 int i = low;// 左指针 int j = mid + 1;// 右指针 int k = 0; // 把较小的数先移到新数组中 while(i<=mid&&j<=hight){ if(a[i]<a[j]){ b[k++]=a[i++]; }else { b[k++]=a[j++]; } } //将剩余的部分方入数组 // 左部分有数组 while (i<=mid) { b[k++]=a[i++]; } //右部分有数组 while (j<=hight) { b[k++]=a[j++]; } // 把新数组中的数覆盖nums数组 for (int k2 = 0; k2 < b.length; k2++) { a[low+k2]=b[k2]; } }
三、时间复杂度
归并排序的形式就是一棵二叉树,它需要遍历的次数就是二叉树的深度,而根据完全二叉树的可以得出它的时间复杂度是O(n*log2n)。
四、空间复杂度
算法处理过程中,需要一个大小为n的临时存储空间用以保存合并序列。
五、算法稳定性
在归并排序中,相等的元素的顺序不会改变,所以它是稳定的算法。
