结对开发 二维数组的最大子数组和

题目：在原有的一位数组上进行扩展，求二位数组的最大子数组的和：

题目:返回一个二维整数数组中最大子数组的和。

要求： 输入一个二维整形数组，数组里有正数也有负数。

         数组中连续的一个或多个整数组成一个子数组，每个子数组都有一个和。

         求所有子数组的和的最大值。

结对编程要求： 两人结对完成编程任务。 一人主要负责程序分析，代码编程。

                    一人负责代码复审和代码测试计划。

                   发表一篇博客文章讲述两人合作中的过程、体会以及如何解决冲突(附结对开发的工作照)。

结对开发过程：

    这次的编程开发是基于上次的以为数组，我和我的搭档@快乐的小菜鸟开始了认真的讨论，再结合课堂上的同学讨论，如何能将二维数组转化为一位数组，降低时间复杂度，这种方法的特殊边界要考虑，首先求出p[i][j]，表示以（0,0）为起点，以(i,j)为终点的的连续子数组的和，起点是第a行，终点是第c行，然后转换为一维连续子数组的和；首先应该找出p[i][j],具体代码如下：

参考代码：

#include <iostream>
using namespace std;

int maxSubArray(int **a,int n,int m)
{
  int **p=new int*[n];
  int i,j;
  if(m==0||n==0)
    return 0;
  //计算p[i][j]    
  for(i=0;i<n;i++)
  {
    p[i]=new int[m];
    for(j=0;j<m;j++)
    {
      if(i==0)
      {
        if(j==0)
          p[i][j]=a[i][j];
        else
          p[i][j]=p[i][j-1]+a[i][j];
      }
      else
      {
        if(j==0)
          p[i][j]=p[i-1][j]+a[i][j];
        else
          p[i][j]=p[i][j-1]+p[i-1][j]-p[i-1][j-1]+a[i][j];
      }
    }
  }
  //计算二维数组最大子数组的和
  int temp;
  int max=a[0][0];
  int ans;
  //如果m==1
  if(m==1)
  {
    for(i=0;i<n;i++)
    {
      for(j=i;j<n;j++)
      {
        if(i==0)
        {
          temp=p[j][m-1];
        }
        else
        {
          temp=p[j][m-1]-p[i-1][m-1];
        }
        if(ans<temp)
          ans=temp;
      }
    }
  }
  else
  {
    for(i=0;i<n;i++)
    {
      for(j=i;j<n;j++)
      {
        if(i==0)
        {
          temp=p[j][m-1]-p[j][m-2];
        }
        else
        {
          temp=p[j][m-1]-p[j][m-2]-p[i-1][m-1]+p[i-1][m-2];
        }
        for(int k=m-2;k>=0;k--)
        {
          if(temp<0)
            temp=0;
          if(i==0)
          {
            if(k==0)
              temp+=p[j][k];
            else
              temp+=p[j][k]-p[j][k-1];
          }
          else
          {
            if(k==0)
              temp+=p[j][k]-p[i-1][k];
            else
              temp+=p[j][k]-p[j][k-1]-p[i-1][k]+p[i-1][k-1];
          }
          if(ans<temp)
            ans=temp;
        }
      }
    }
  }
  return ans;
}

int main()
{
  int n,m;
  printf("请输入二维数组的行数和列数：
");
  scanf("%d %d",&n,&m);
  int i,j;
  int **a=new int*[n];
  printf("请输入%d*%d个二维数组元素：
",n,m);
  for(i=0;i<n;i++)
  {
    a[i]=new int[m];

    for(j=0;j<m;j++)
    {
      scanf("%d",&a[i][j]);
    }
  }
  int ans=maxSubArray(a,n,m);
  printf("二维数组的最大子数组之和是：%d
",ans);
  return 0;
}

程序结果测试：

  

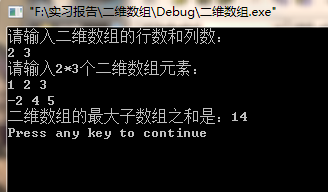
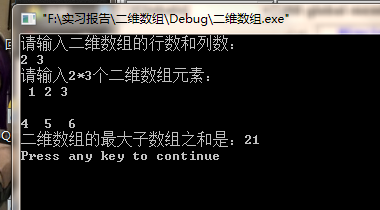
实验结束的感想：

   当时看到的时候，感觉应该不是很难，但是想了半天也想不出来，直到老师让同学去讲台讲了他们的想法，才给了我们一点启发，然后再课下找到了一点资料，最后才勉强在别人的基础上有了一点结果，才明白什么事都不能想当然。