1.尼克的任务

#include <stdio.h> #include <memory.h> #include <math.h> #include <string> #include <vector> #include <set> #include <stack> #include <queue> #include <algorithm> #include <map> #define I scanf #define OL puts #define O printf #define F(a,b,c) for(a=b;a<c;a++) #define FF(a,b) for(a=0;a<b;a++) #define FG(a,b) for(a=b-1;a>=0;a--) #define LEN 10010 #define MAX 1<<30 #define V vector<int> using namespace std; typedef struct node{ int s,e; }node; node t[LEN]; int dp[LEN]; int st[LEN]; int cmp(node a,node b){ //用于递减排序,重定义大于符号 return a.s>b.s; } int main(){ // freopen("尼克的任务.txt","r",stdin); int n,k,i,j,m; I("%d %d",&n,&k); F(i,1,k+1){ I("%d%d",&t[i].s,&t[i].e); st[t[i].s]++; //记录起始时间点 } sort(t+1,t+1+k,cmp); //让时间结构体递减排序 for(i=n;i>=1;i--){ //对于时间,从后往前循环 if(st[i]==0){ //从后往前循环的过程中,没有没有查询到起始时间点 dp[i]=dp[i+1]+1; //dp数组表示 从i时刻往后的空闲时间 }else{ //查询到了起始时间点 for(m=1;m<=k;m++){ //对所有任务进行遍历 if(t[m].s==i){ //遍历到的任务的其实时间点是当前时间点 dp[i]=max(dp[i],dp[i+t[m].e]); } //找出所有i时间开始的任务,记录他们结束时 最大的空闲时间 } } } O("%d ",dp[1]); return 0; }
2.括号匹配
主代码:
//对角线初始化 for(i=0;i<len;i++) dp[i][i]=1; //动态规划 for(v=1;v<len;v++){ //定义间隔 for(i=0;i+v<len;i++){ //定义起始下标 int j=i+v; //定义结束下标 dp[i][j]=MAX; if(cmp(str[i],str[j])) //如果i到j的括号可以匹配 dp[i][j]=min(dp[i][j], dp[i+1][j-1]); //就对比中间的情况 :dp[i+1][j-1] //(在这里我们注意到特殊情况dp[0][1],中间情况是dp[1][0], 因为dp矩阵是上三角矩阵,为0,满足定义 for(k=i;k<j;k++){ //进行子情况剖分 dp[i][j]=min(dp[i][j], dp[i][k]+dp[k+1][j]); } } }
完整代码:

#include<cstdio> #include<iostream> #include<string.h> #define I scanf #define OL puts #define O printf #define F(a,b,c) for(a=b;a<c;a++) #define FF(a,b) for(a=0;a<b;a++) #define FG(a,b) for(a=b-1;a>=0;a--) #define LEN 300 #define MAX 1<<30 #define V vector<int> using namespace std; int dp[LEN][LEN]; bool cmp(int a, int b){ if( (a=='[' && b==']') || (a=='(' && b==')') ){ return 1; } return 0; } int main(){ // freopen("D:/CbWorkspace/动态规划/括号匹配.txt","r",stdin); int i,j,k,v,n; char str[LEN]; I("%d",&n); while(n--){ I("%s",str); int len=strlen(str); memset(dp,0,sizeof(dp)); //对角线初始化 for(i=0;i<len;i++) dp[i][i]=1; //动态规划 for(v=1;v<len;v++){ //定义间隔 for(i=0;i+v<len;i++){ //定义起始下标 int j=i+v; //定义结束下标 dp[i][j]=MAX; if(cmp(str[i],str[j])) //如果i到j的括号可以匹配 dp[i][j]=min(dp[i][j], dp[i+1][j-1]); //就对比中间的情况 :dp[i+1][j-1] //(在这里我们注意到特殊情况dp[0][1],中间情况是dp[1][0], 因为dp矩阵是上三角矩阵,为0,满足定义 for(k=i;k<j;k++){ //进行子情况剖分 dp[i][j]=min(dp[i][j], dp[i][k]+dp[k+1][j]); } } } O("%d ",dp[0][len-1]); } return 0; }
dp矩阵示意:
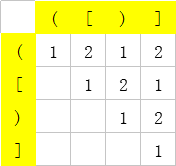
3.整数划分
递归:(类似于把m个苹果放入n个盒子)
int recursion(int m,int n){//表示把m划分成n个数 if(n==1||n==m){ return 1; }else if(m<n){ return 0; }else{ //递归原则:看成 包含 1 与 不包含 1 的两部分 return recursion(m-1,n-1) + //固定第一个数字 1 ,划分 m-1 为 n-1 个数 recursion(m-n,n); //划分出来的 n 个数字全部减 1 , 相当于把 m-n 划分成 n 个数 } }
动态规划:
4.回文字符串
获得一个字符串最长的回文子串长度:

#include <stdio.h> #include <memory.h> #include <math.h> #include <cstring> #include <vector> #include <set> #include <stack> #include <queue> #include <algorithm> #include <map> #define I scanf #define OL puts #define O printf #define F(a,b,c) for(a=b;a<c;a++) #define FF(a,b) for(a=0;a<b;a++) #define FG(a,b) for(a=b-1;a>=0;a--) #define LEN 1001 #define MAX 1<<30 #define V vector<int> using namespace std; int dp[LEN][LEN]; int main(){ freopen("回文字符串.txt","r",stdin); int N,n,i,j,v,ans; I("%d",&N); while(N--){ ans=1; char str[LEN]; I("%s",str); n=strlen(str); memset(dp,0,sizeof(dp)); for(i=0;i<n;i++) dp[i][i]=1; for(v=1;v<n;v++){ for(i=0;i+v<n;i++){ j=i+v; if(str[i]==str[j]){ dp[i][j]=dp[i+1][j-1]+2; ans=max(ans,dp[i][j]) ; } } } O("%d ",ans); } return 0; }
题解:

#include <stdio.h> #include <memory.h> #include <math.h> #include <cstring> #include <vector> #include <set> #include <stack> #include <queue> #include <algorithm> #include <map> #define I scanf #define OL puts #define O printf #define F(a,b,c) for(a=b;a<c;a++) #define FF(a,b) for(a=0;a<b;a++) #define FG(a,b) for(a=b-1;a>=0;a--) #define LEN 1001 #define MAX 1<<30 #define V vector<int> using namespace std; int dp[LEN][LEN]; int main(){ // freopen("回文字符串.txt","r",stdin); int N,n,i,j,v,ans,k; I("%d",&N); while(N--){ ans=1; char str[LEN]; I("%s",str); n=strlen(str); memset(dp,0,sizeof(dp)); for(v=1;v<n;v++){ for(i=0;i+v<n;i++){ j=i+v; if(str[i]==str[j]) dp[i][j]=dp[i+1][j-1]; else dp[i][j]=min(dp[i+1][j],dp[i][j-1])+1; } } O("%d ",dp[0][n-1]); } return 0; }
鸣谢欧阳大佬给的状态转移方程!
