富集分析的原理与实现

一般做完差异分析都会做这一步，目的是找到差异基因富集到的通路，进而与生物学意义联系起来。具体的统计方法很简单，这篇笔记里面的代码可以从零搭建一个富集分析工具。

后台回复20211007获取本文的测试数据和代码，以及（单细胞）转录组分析中可能用到的GO KEGG富集分析代码（这部分本文不演示）。

关于Gene Ontology (GO), KEGG这些背景就不讲了，网上很多资料。

将富集分析中的问题抽象出来，其实就是下图的“摸球”问题。

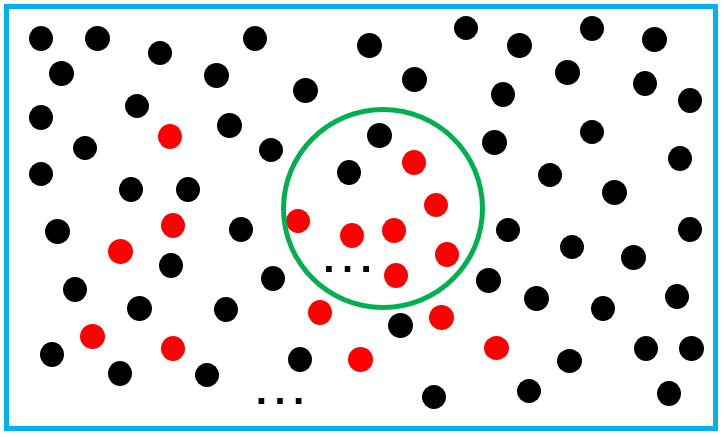
蓝色方框中的球是所有的基因【共N个】，在探究某个特定通路P时，通路里面涉及到的基因用红色表示【共M个】。绿色圆圈是一次摸球事件，用来表示做了一次差异分析得到的基因【共n个】，这些基因中，有属于通路P的(红色球)【共k个】，有不属于的(黑色球)。

用摸球问题中的语言再描述一次：袋子中共有黑球和红球N个，其中红球M个。某次抽样中，一共摸球n个，其中红球k个，问在这次摸球中，红球的占比是否显著高于袋子中红球的占比？
（以前学摸球问题/超几何分布的时候，可能只求概率，没有进一步到这个统计检验）

回答这个问题，需要求出问题中这个事件的概率以及更极端事件的概率之和，也就是p值，小于0.05或者0.01就能认为是显著了。

1. 一个通路，计算p值

接下来以一个GO term (GO_extracellular_matrix_organization)为例，计算p值。
用的通路基因集是小鼠 GO BP的基因集，差异基因集是单细胞转录组分析中一个cluster的高表达基因

library(tidyverse)
library(clusterProfiler)

gmt.df=read.gmt("Mm.c5.bp.v7.1.SYMBOL.gmt")
deg=read.table("test_deg.txt",header = T,sep = "	",stringsAsFactors = F)
deg=deg[deg$gene %in% gmt.df$gene,]

这种情况下，前面说的几个参数的值如下：

• 全部球的个数/全部基因数：
  N=length(unique(gmt.df$gene))
• 全部红球的个数/通路基因集的基因数：
  one.set=gmt.df[ gmt.df$term %in% c("GO_extracellular_matrix_organization") ,] M=length(one.set$gene)
• 摸球数/差异基因数：
  n=length(deg$gene)
• 摸球中红球的个数/差异基因中属于这个通路的基因数：
  k=sum(deg$gene %in% one.set$gene)

N M n k的值分别为: 23210, 271, 47, 6

求p值之前，先看一下满足N M n这三个参数的超几何分布，在不同的k值之下的概率：

df1=data.frame(x=1:47,y=dhyper(x=1:47, M, N-M, n))
df1%>%ggplot(aes(x,y))+geom_point()+
  geom_line()+
  geom_vline(xintercept=k,color="red",linetype=5)+  #这里k等于6，其作为阈值
  theme_bw()+
  theme(panel.grid = element_blank())

dhyper()用来求概率，四个参数分别是：摸球中红球个数的向量，袋中红球数，袋中黑球数，摸球数

我们要计算的就是红线以及右边那些红球数对应的概率之和，如下：

> phyper(k-1,M, N-M, n, lower.tail=FALSE)
[1] 1.722659e-05

当lower.tail=FALSE，计算的是P[X > x]，即大于第一个参数的概率之和。上面的代码第一个参数写的是k-1，因为我们需要求k以及k右边的概率之和。

以上是对一个通路求p值

---

2. 多个通路，依次计算p值

如果是多个通路，需要循环操作，依次对每个通路进行富集分析。
下面的演示用到的差异基因集和GO BP基因集同上

分析哪些pathway？要满足两个条件：

• 通路里面基因的数量满足一定要求
• 至少和deg有基因交集

下面的代码就是对通路做过滤的

bp.stat=as.data.frame(table(gmt.df$term))
colnames(bp.stat)[1]="pathway"
bp.stat=bp.stat%>%filter(Freq >= 2 & Freq <= 2000)

tmp.df=gmt.df
tmp.df$TF=tmp.df$gene %in% deg$gene
tmp.stat=as.data.frame(tmp.df %>% dplyr::group_by(term) %>% dplyr::summarize(counts=sum(TF)))
tmp.stat=tmp.stat%>%filter(counts > 0)
keep.pw=sort(intersect(bp.stat$pathway,tmp.stat$term))

下面就是循环求p值了

N=length(unique(gmt.df$gene))
n=length(deg$gene)
term=c()
pvalue=c()

for (i in keep.pw) {
  one.set=gmt.df[ gmt.df$term %in% i ,]
  M=length(one.set$gene)
  k=sum(deg$gene %in% one.set$gene)
  one.pvalue=phyper(k-1,M, N-M, n, lower.tail=FALSE)
  term=append(term,i)
  pvalue=append(pvalue,one.pvalue)
}

my_go_res=data.frame(term=term,pvalue=pvalue)
my_go_res=my_go_res%>%arrange(pvalue)

到这会儿还没有结束，还差一个FDR

---

3. 计算矫正p值

FDR, False Discovery Rates。为什么要控制FDR，降低假阳性。
这里用到的是The Benjamini-Hochberg method

The Benjamini-Hochberg method

假设我们对10个通路做了富集分析，我们会先得到10个p值：

1. 将这10个p值从小到大排序
2. 从1到10给这些p值排序
3. 最大的FDR adjusted p value（第10位）等于原来最大的那个p值
4. 第9位的FDR adjusted p value等于这两个值中的较小值：
   ①前一位矫正的p值；
   ②当前未矫正的p值 * （p值总个数/当前位数）
5. 重复第4步，直到第1位

代码如下：

fdr=c()
for (i in dim(my_go_res)[1]:1) {
  if (i==dim(my_go_res)[1]) {
    tmpfdr=my_go_res$pvalue[i]
  }else{
    tmpfdr=min(tmpfdr,my_go_res$pvalue[i] * (dim(my_go_res)[1] / i))
  }
  fdr=append(fdr,tmpfdr)
}
my_go_res$p.adj=rev(fdr)

到这儿富集分析的完整流程才算结束

---

4. 轮子有现成的

当然，这个算法已经非常常见了，clusterProfiler的enricher()就能够自定义基因集做富集分析。使用如下：

deg_gmt=clusterProfiler::enricher(deg$gene,TERM2GENE = gmt.df,minGSSize = 2,maxGSSize = 2000)
go_res=deg_gmt@result

和上面的结果是一模一样的。

今天的内容就到这里，后台回复20211007获取本文的测试数据和代码，以及（单细胞）转录组分析中可能用到的GO KEGG富集分析代码（这部分本文不演示）。

ref

• 超几何分布检验（hypergeometric test）：https://blog.csdn.net/linkequa/article/details/86491665
• 富集分析的p值是怎么算出来的？：公众号【YuLabSMU】
• R tips 富集分析及其p值在R中的计算：公众号【生信菜鸟团】
• False Discovery Rates, FDR, clearly explained：https://www.youtube.com/watch?v=K8LQSvtjcEo&t=909s&ab_channel=StatQuestwithJoshStarmer

因水平有限，有错误的地方，欢迎批评指正！