曼哈顿距离
曼哈顿距离又称马氏距离(Manhattan distance),还见到过更加形象的,叫出租车距离的。具见上图黄线,应该就能明白。
计算距离最简单的方法是曼哈顿距离。假设,先考虑二维情况,只有两个乐队 x 和 y,用户A的评价为(x1,y1),用户B的评价为(x2,y2),那么,它们之间的曼哈顿距离为 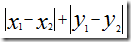
基本概念
-
启发式搜索:启发式搜索就是在状态空间中的搜索对每一个搜索的位置进行评估,得到最好的位置,再从这个位置进行搜索直到目标。这样可以省略大量无畏的搜索路径,提到了效率。在启发式搜索中,对位置的估价是十分重要的。采用了不同的估价可以有不同的效果。
-
估价函数:从当前节点移动到目标节点的预估费用;这个估计就是启发式的。在寻路问题和迷宫问题中,我们通常用曼哈顿(manhattan)估价函数(下文有介绍)预估费用。
-
start:路径规划的起始点,也是机器人当前位置或初始位置A
-
goal:路径规划的终点,也是机器人想要到达的位置B
-
g_score:当前点到沿着start点A产生的路径到A点的移动耗费
-
h_score:不考虑不可通过区域,当前点到goal点B的理论移动耗费,我们这里使用的是Manhattan计算方式
-
f_score:g_score+h_score,通常也写为F=G+H
-
开启列表openset:寻路过程中的待检索节点列表
-
关闭列表closeset:不需要再次检索的节点列表
-
追溯表comaFrom:存储父子节点关系的列表,用于追溯生成路径。
算法解析
如图1,绿色点为start设为A,红色点为goal设为B,蓝色点为不可通过的障碍物,黑色点为自由区域。目标是规划从A到B的路径。

开始搜索
- 搜索的从A点开始,首先将A点加入开启列表,此时取开启列表中的最小值,初始阶段开启列表中只有A一个节点,因此将A点从开启列表中取出,将A点加入关闭列表。
-
取出A点的相邻点,将相邻点加入开启列表。如图2所示,此时A点即为相邻点的父节点。图中箭头指向父节点。将相邻点与A点加入追溯表中。
 图2
图2
计算耗费评分
对相邻点,一次计算每一点的g_score,h_score,最后得到f_score。如图3,节点的右下角为g_score值,左下角为h_score值,右上角为f_score。

选最小值,再次搜索
- 选出开启列表中的F值最小的节点,将此节点设为当前节点,移出开启列表,同时加入关闭列表。如图4所示。
-
取出当前点的相邻点,当相邻点为关闭点或者墙时,不操作。此外,查看相邻点是否在开启列表中,如不在开启列表中将相邻点加入开启列表。如相邻点已经在开启列表中,则需要进行G值判定
 图4
图4
G值判定
- 对于相邻点在开启列表中的,计算相邻点的G值,计算按照当前路径的G值与原开启列表中的G值大小。如果当前路径G值小于原开启列表G值,则相邻点以当前点为父节点,将相邻点与当前点加入追溯表中。同时更新此相邻点的H值。如果当前路径G值大于等于原开启列表G值,则相邻点按照原开启列表中的节点关系,H值不变。因为图示中,当前点G值比原开启列表G值大,因此节点关系按照原父子关系和F值。
计算耗费评分,选最小值
-
此时计算开启列表中F值最小的点,将此节点设为当前节点,并列最小F值的按添加开启列表顺序,以最新添加为佳。
 图5
图5
重复搜索判定工作
- 直到当goal点B加入开启列表中,则搜索完成。此时事实上生成的路径并一定是最佳路径,而是最快计算出的路径。若判定标准改为当goal点B加入关闭列表中搜索完成,则得出路径是最佳路径,但此时计算量较前者大。
-
当没有找到goal点,同时开启列表已空,则搜索不到路径。结束搜索。
 图6
图6
生成路径
-
由goal点B向上逐级追溯父节点,追溯至起点A,此时各节点组成的路径即使A*算法生成的最优路径。
 图7
图7
A*算法总结(Summary of the A* Method)
Ok ,现在你已经看完了整个的介绍,现在我们把所有步骤放在一起:
1. 把起点加入 open list 。
2. 重复如下过程:
a. 遍历 open list ,查找 F 值最小的节点,把它作为当前要处理的节点。
b. 把这个节点移到 close list 。
c. 对当前方格的 8 个相邻方格的每一个方格?
◆ 如果它是不可抵达的或者它在 close list 中,忽略它。否则,做如下操作。
◆ 如果它不在 open list 中,把它加入 open list ,并且把当前方格设置为它的父亲,记录该方格的 F , G 和 H 值。
◆ 如果它已经在 open list 中,检查这条路径 ( 即经由当前方格到达它那里 ) 是否更好,用 G 值作参考。更小的 G 值表示这是更好的路径。如果是这样,把它的父亲设置为当前方格,并重新计算它的 G 和 F 值。如果你的 open list 是按 F 值排序的话,改变后你可能需要重新排序。
d. 停止,当你
◆ 把终点加入到了 open list 中,此时路径已经找到了,或者
◆ 查找终点失败,并且 open list 是空的,此时没有路径。
3. 保存路径。从终点开始,每个方格沿着父节点移动直至起点,这就是你的路径。
伪代码:
// a* 伪代码 function A*(start, goal) //初始化关闭列表,已判定过的节点,进关闭列表。 closedSet := {} // 初始化开始列表,待判定的节点加入开始列表。 // 初始openset中仅包括start点。 openSet := {start} // 对每一个节点都只有唯一的一个父节点,用cameFrom集合保存节点的子父关系。 //cameFrom(节点)得到父节点。 cameFrom := the empty map // gScore估值集合 gScore := map with default value of Infinity gScore[start] := 0 // fScore估值集合 fScore := map with default value of Infinity fScore[start] := heuristic_cost_estimate(start, goal) while openSet is not empty //取出F值最小的节点设为当前点 current := the node in openSet having the lowest fScore[] value //当前点为目标点,跳出循环返回路径 if current = goal return reconstruct_path(cameFrom, current) openSet.Remove(current) closedSet.Add(current) for each neighbor of current if neighbor in closedSet continue // 忽略关闭列表中的节点 // tentative_gScore作为新路径的gScore tentative_gScore := gScore[current] + dist_between(current, neighbor) if neighbor not in openSet openSet.Add(neighbor) else if tentative_gScore >= gScore[neighbor] continue //新gScore>=原gScore,则按照原路径 // 否则选择gScore较小的新路径,并更新G值与F值。同时更新节点的父子关系。 cameFrom[neighbor] := current gScore[neighbor] := tentative_gScore fScore[neighbor] := gScore[neighbor] + heuristic_cost_estimate(neighbor, goal) return failure //从caomeFrom中从goal点追溯到start点,取得路径节点。 function reconstruct_path(cameFrom, current) total_path := [current] while current in cameFrom.Keys: current := cameFrom[current] total_path.append(current) return total_path
参考资料:
A*算法详解:
http://blog.csdn.net/hitwhylz/article/details/23089415
A*算法详解:
http://www.360doc.com/content/16/1201/12/99071_610999046.shtml
A*详解:




