Luogu P3647 连珠线 题解报告

题目传送门

【题目大意】

 

【思路分析】

好的这道题目我在换根DP的部分卡了一个世纪……所以设状态真的很重要，我因为状态设的不好，然后换根的时候就很复杂QAQ

我来讲一下一个学长的做法叭QwQ

最后的连接情况是一棵树，首先我们要发现两个性质，就是在树中蓝线一定是连接在父子之间，并且连续的一段蓝线一定为偶数。

因为蓝线是删除了一条红线之后加入的，所以不可能存在类似下左图这种形状的连接方式，下右图这种连接方式才是合法的

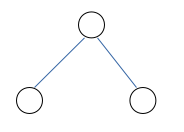
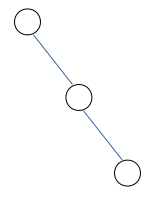
然后因为每次添加两根蓝线(我们称这两根蓝线为一组)，所以显然连续的蓝线数量必须是偶数。

总体思路是设1为根先DP一遍，然后换根，重要的是如何设状态可以在换根的时候方便转移。

我们设$f[x]$表示以$x$为根的子树的最大分数，注意此时这个子树可以单独出来，即子树中的蓝线数量为偶数。

$d[x][0]$结构体记录与$x$相连的，以$x$为根的子树中的边中最大的边的值和这条边连接的$x$的儿子，$d[x][1]$记录次大值及对应的儿子。当然记录的值保证更优，即记录下的儿子$y$在下左图的连接方式比下右图的连接方式更优。

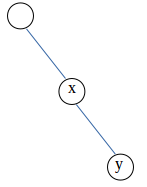
转移见代码及注释

【代码实现】

#include<cstdio>
#include<iostream>
#include<cstring>
#include<algorithm>
#include<cmath>
#include<queue>
#define g() getchar()
#define rg register
#define go(i,a,b) for(rg int i=a;i<=b;i++)
#define back(i,a,b) for(rg int i=a;i>=b;i--)
#define db double
#define ll long long
#define il inline
#define pf printf
#define mem(a,b) memset(a,b,sizeof(a))
#define E(i,x) for(rg int i=hd[x];i;i=e[i].nxt)
#define t(i) e[i].to
#define w(i) e[i].w
using namespace std;
int fr(){
    int w=0,q=1;
    char ch=g();
    while(ch<'0'||ch>'9'){
        if(ch=='-') q=-1;
        ch=g();
    }
    while(ch>='0'&&ch<='9') w=(w<<1)+(w<<3)+ch-'0',ch=g();
    return w*q;
}
const int N=200002;
const int INF=1e9+7;
int n,ed,hd[N],f[N],ans;
struct edge{
    int nxt,to,w;
}e[N<<1];
struct node{
    int frm,v;
}d[N][2];
il void build(rg int u,rg int v,rg int w){
    e[++ed]=(edge){hd[u],v,w};hd[u]=ed;
    swap(u,v);
    e[++ed]=(edge){hd[u],v,w};hd[u]=ed;
    return;
}
il void update(rg int x,rg int y,rg int w){
    if(w>=d[x][0].v) d[x][1]=d[x][0],d[x][0]=(node){y,w};
    else if(w>d[x][1].v) d[x][1]=(node){y,w};
    return;
}
il void dp(rg int x,rg int fa){
    d[x][0].v=d[x][1].v=-INF;f[x]=0;
    E(i,x){
        if(t(i)==fa) continue;
        dp(t(i),x);
        rg int as=max(f[t(i)],f[t(i)]+d[t(i)][0].v+w(i));//选择更优的连接方式
        f[x]+=as;update(x,t(i),f[t(i)]+w(i)-as);
        //这里的update有一个很巧妙的转化来判断那种连接方式更优
    }    return;
}
il void dfs(rg int x,rg int fa){
    ans=max(ans,f[x]);
    E(i,x){
        if(t(i)==fa) continue;
        node d0=d[t(i)][0],d1=d[t(i)][1];//记录原来的值
        rg int t1=f[t(i)],t2=max(t1,t1+d[t(i)][0].v+w(i));//找原来是怎么连接的
        rg int f1=f[x]-t2,f2=(d[x][0].frm==t(i));//特判一下特殊情况
        rg int as=max(f1,f1+d[x][f2].v+w(i));//把原本的父亲变为儿子连上去
        f[t(i)]+=as;update(t(i),x,f1+w(i)-as);//更新d数组的值
        dfs(t(i),x);
        f[t(i)]=t1;d[t(i)][0]=d0;d[t(i)][1]=d1;//还原原来的值
    }
    return;
}
int main(){
    //freopen("1.in","r",stdin);
    //freopen("1.out","w",stdout);
    n=fr();
    go(i,1,n-1){
        rg int u=fr(),v=fr(),w=fr();
        build(u,v,w);
    }
    dp(1,0);ans=-INF;dfs(1,0);
    pf("%d
",ans);
    return 0;
}