目录
题目完成进度
15/22
首先是几种算数位运算:

这些运算不局限于逻辑运算,均可作用于二进制整数。
补码
移位运算
1.左移
在二进制表示下把数字同时向左移动,低位以0填充,高位越界后舍弃。
$$1<<n=2^n,n<<1=2n$$
2.算数右移
算数右移等于除以2向下取整,即$n>>1=lfloorfrac{n}{2.0} floor$
注意:“整数/2”在C++中实现为“除以2向0取整”,即$(-3)/2=-1,3/2=1$
3.逻辑右移
逻辑右移与算数右移的区别在于算数右移时高位以补码的符号位填充,逻辑右移时高位以0填充。C++语法中没有规定右移的实现方式,使用算数右移还是逻辑右移由编译器决定,一般使用算数右移。
上一道例题——
CH90 64位整数除法
二进制状态压缩
二进制状态压缩,是指将一个长度为$m$的$bool$数组用一个$m$为二进制整数表示并存储的方法。利用以下操作可以实现原$bool$数组中对应下标元素的存取。
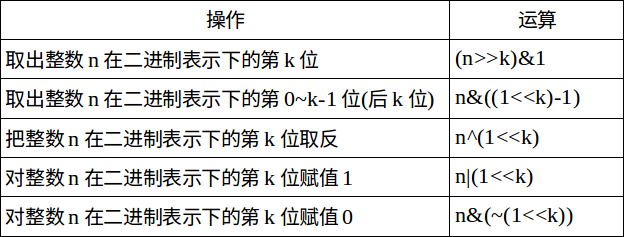
这种方法运算简便,并且节省了程序运行的时间和空间。
例题走起——
CH91 最短Halmilton路径
提醒:一些运算符优先级从高到低的顺序如下表所示。
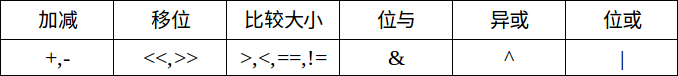
成对变换
lowbit运算
一个实际问题的各种可能情况构成的集合通常称为“状态空间”,而程序的运行则是对于状态空间的遍历,算法和数据结构则是通过划分、归纳、提取、抽象来帮助提高程序遍历状态空间的效率。递推和递归就是程序遍历状态空间的两种基本方式,枚举和模拟就是将面前的状态空间按照一定的顺序“直接地”交给程序遍历的算法。
先上两道例题——
CH95 费解的开关
poj1958 Strange Towers of Hanoi
前缀和
前缀和在题目中非常有用,一维前缀和常用于求某段区间内的数的和,二维前缀和则用于求某块区域内的数的和。
上例题——
递归也是一种常用的算法,思想与分治类似,把一个大问题分成若干个小的子问题解决,可以有效地降低程序的复杂度。
两道例题——
二分法是一种非常精妙的算法,二分的基础用法是在单调序列或单调函数中进行查找,因此当问题的答案具有单调性时,就可以通过二分把求解转化为判定(判定的复杂度小于求解)。二分的实现方法多种多样,但是其细节之处需要仔细考虑。对于整数域上的二分,需要注意终止边界、左右区间取舍时的开闭情况,避免漏掉答案或造成死循环;对于实数域上的二分,需要注意精度问题。
整数域上的二分
实数域上的二分
三分求单峰函数极值
二分答案转化为判定
例题——
Innovative Business
之前有整理过各种排序的基础知识哦,放个链接吧。这里讲一讲常见的可以与排序有关的问题。
离散化
上一道例题——
中位数
三道例题——
CH104 货仓选址
CH105 七夕祭
第$k$大数
逆序对
例题走起——
CH108 奇数码问题
倍增是指,在进行递推时,如果状态空间很大,通常的线性递推无法满足时间与空间复杂度的要求,那么我们可以通过成倍增长的方式,只递推状态空间中在2的整数次幂位置上的值作为代表。当需要其他位置上的值时,我们通过“任意整数可以表示成若干个2的次幂项的和”这一性质,使用之前求出的代表值拼成所需的值。所以使用倍增算法也要求我们递推的问题的状态空间关于2的次幂具有可划分性。
来一道例题——
CH109 Genius ACM
ST算法
贪心是一种在每次决策时采取当前意义下最优策略的算法,因此,使用贪心法要求问题的整体最优性可以由局部最优性导出。贪心算法的正确性的证明手段有:
1.微扰(邻项交换)
证明在任意局面下,任何对局部最优策略的微小改变都会造成整体结果变差。经常用于以“排序”为贪心策略的证明。
2.范围缩放
证明任何对局部最优策略作用范围的扩展都不会造成整体结果变差。
3.决策包容性
证明在任何局面下,作出局部最优决策以后,在问题状态空间中的可达集合包含了作出其他任何决策后的可达集合。换言之,这个局部最优策略提供的可能性包含其他所有策略提供的可能性。
4.反证法
5.数学归纳法
上例题——
poj1328 Radar Installation
Luogu P1080 国王游戏