P3043 [USACO12JAN]牛联盟Bovine Alliance——并查集

题目描述

给出n个点m条边的图，现把点和边分组，每条边只能和相邻两点之一分在一组，点可以单独一组，问分组方案数。

（友情提示：每个点只能分到一条边，中文翻译有问题，英文原版有这样一句：The cows in each of the N  farms were initially instructed to build a trail to exactly one other farm）

思路

　　这题只要多画一画图，找一找性质就可以了。

　　我们先从一条链考虑：

 　　可以看出，答案显然是四种，即四个点分别是单身狗的情况。

　　我们再考虑一棵树：

　　、

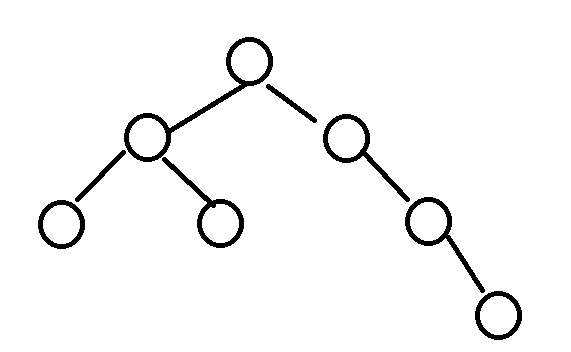　　显然确定了一个点不分到边后，情况就确定了。

　　我们得出第一条性质：对于一个n个点，n-1条边的图，答案就是n。

　　我们再来考虑环：

 　　

　　  还是很显然：确定了一条边的分组后，其它的边的分组也是确定的，答案为2。

　　那么我们可以得出：一个联通块的点和边要么是一棵树，要么是一棵基环树，因为如果m>n，是不存在合法方案的。

　　我们考虑用并查集来写，分别维护处连通块中的点数和边数，用乘法原理计数即可。

code

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<vector>
using namespace std;
const int N=100010;
const int p=1000000007;
int n,m;
struct node
{
    int u,v;
}g[N];
int father[N];
int sum1[N],sum2[N];

inline int find(int x){return x==father[x]?x:father[x]=find(father[x]);}
inline int merge(int x,int y)
{
    father[y]=x;sum1[x]+=sum1[y];sum2[x]+=sum2[y]+1;
    sum1[y]=0;sum2[y]=0;
}

int ans=1;

int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++)father[i]=i,sum1[i]=1;
    for(int i=1;i<=m;i++)
    {
        int x,y;scanf("%d%d",&x,&y);
        int r1=find(x),r2=find(y);
        if(r1!=r2)merge(r1,r2);
        else sum2[r1]++;
    }
    for(int x=1;x<=n;x++)
    {
        if(x!=find(x))continue;
        int r=find(x);
        if(sum1[r]==sum2[r])ans=(ans*2)%p;
        else
        {
            ans=(long long)ans*sum1[r]%p;
        }
    }
    cout<<ans%p;        
}