CF600E Lomsat gelral——线段树合并/dsu on tree

题目描述

　　一棵树有$n$个结点，每个结点都是一种颜色，每个颜色有一个编号，求树中每个子树的最多的颜色编号的和。

　　这个题意是真的窒息。。。具体意思是说，每个节点有一个颜色，你要找的是每个子树中颜色的众数（可能有多个），比如子树中有$3个2,3个1，3个5，那么2,1,5都是众数，答案为2+1+5=8$。

思路

做法一：

　　线段树合并。权值线段树覆盖颜色$1->100000，用sum$表示颜色最多出现的次数，$ans$表示答案。分$3种情况pushup$即可。

1. 左右子树$sum$相等
2. 左边$>$右边
3. 左边$<$右边

　　$dfs的时候merge$一下即可。

code

#include<iostream>
#include<algorithm>
#include<cstring>
#include<cstdio>
#include<vector> 
#define smid (l+r>>1)
#define I inline 
using namespace std;
typedef long long LL;
const int N=100010;
LL col[N];
LL maxcol;
int n;
int ls[N*40],rs[N*40],cnt,rt[N];
LL sum[N*40],ans[N*40];
vector<int>g[N];
LL out[N];

I void pushup(int now)
{
    if(sum[ls[now]]==sum[rs[now]])
    {
        sum[now]=sum[ls[now]];
        ans[now]=ans[ls[now]]+ans[rs[now]];
    }
    else if(sum[ls[now]]<sum[rs[now]])
    {
        sum[now]=sum[rs[now]];
        ans[now]=ans[rs[now]];
    }
    else
    {
        sum[now]=sum[ls[now]];
        ans[now]=ans[ls[now]];
    }
}

I void modify(int &now,int l,int r,int pos)
{
    if(!now)now=++cnt;
    if(l==r)
    {
        sum[now]++;ans[now]=l;
        return;
    }
    if(pos<=smid)modify(ls[now],l,smid,pos);
    else modify(rs[now],smid+1,r,pos);
    pushup(now);
}

I int merge(int x,int y,int l,int r)
{
    if(!x||!y)return x+y;
    if(l==r)
    {
        sum[x]+=sum[y];ans[x]=l;
        return x;
    }
    ls[x]=merge(ls[x],ls[y],l,smid);
    rs[x]=merge(rs[x],rs[y],smid+1,r);
    pushup(x);
    return x;
}

I void dfs(int u,int fa)
{
    for(int i=0;i<g[u].size();i++)
    {
        int v=g[u][i];
        if(v==fa)continue;
        dfs(v,u);
        merge(rt[u],rt[v],1,100000);
    }
    modify(rt[u],1,100000,col[u]);
    out[u]=ans[rt[u]];
}

int main()
{
    ios::sync_with_stdio(false);
    cin>>n;
    for(int i=1;i<=n;i++)
    {
        cin>>col[i];
        rt[i]=i;cnt++;
    }
    for(int i=1;i<n;i++)
    {
        int x,y;cin>>x>>y;
        g[x].push_back(y);g[y].push_back(x);
    }
    dfs(1,0);
    for(int i=1;i<=n;i++)
    {
        cout<<out[i]<<" ";
    }
}

洛谷上交不了，必须到$CF$上交，但是$CF$上不给用scanf("%lld")，就加了$cin$加速。

做法二：

　　树上启发式合并。这里当做板子题来讲。$dsu on tree$是个啥？其实就是优化的暴力，对于一棵树，我们定义节点$u的重儿子son[u]为其size$最大的儿子，其余为轻儿子。这个算法主要用于：

1. 只有对子树的询问
2. 没有修改操作

　　回到这个题目：首先我们考虑暴力$dfs$：遍历每个节点的子树，统计颜色出现的个数，得出当前的的答案，再清空当前点的影响，继续$dfs$，这个算法是$O(n^2)$的，于是我们使用一些重链剖分的性质，搞一个树上启发式合并。具体流程如下：

1. $dfs$遍历每个节点
2. 先递归所有轻儿子，跑到底层，不保留这一次$dfs$的答案
3. 递归重儿子，保留这一次$dfs$的答案
4. 重儿子所在子树被处理完了，而且又保留了答案，只剩下当前节点的轻儿子了
5. 暴力统计所有轻儿子所在子树的答案
6. 通过上面两步得出当前点的答案
7. 如果是轻儿子就清空当前点对答案的影响

主体框架

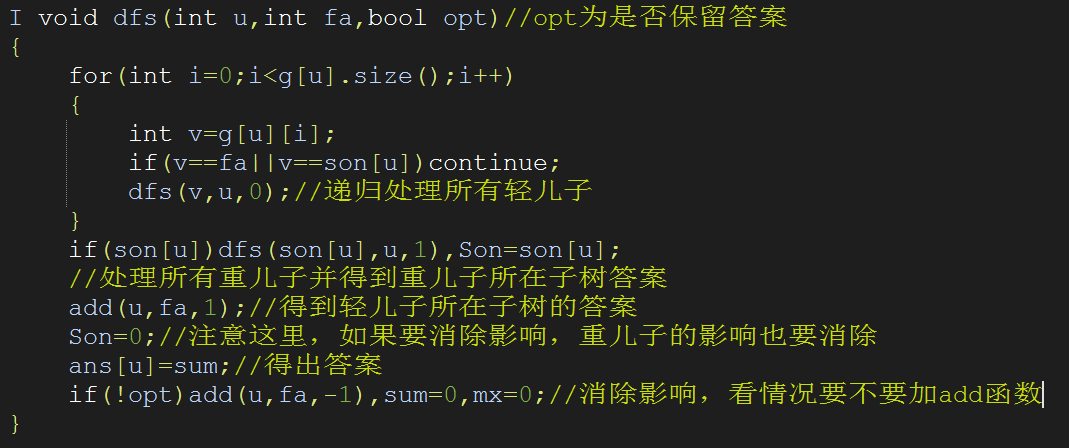
code（比较板子）

#include<iostream>
#include<algorithm>
#include<vector>
#include<cstring>
#include<cstdio>
#define I inline
using namespace std;
const int N=100010;
typedef long long LL;
int sz[N],son[N],n,col[N],Son;
vector<int>g[N];
LL cnt[N],mx,ans[N],sum;

I int read()
{
    int x=0,f=1;char ch=getchar();
    while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
    while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
    return x*f;
}

I void gets(int u,int fa)
{
    sz[u]=1;
    for(int i=0;i<g[u].size();i++)
    {
        int v=g[u][i];
        if(v==fa)continue;
        gets(v,u);
        sz[u]+=sz[v];
        if(sz[v]>sz[son[u]])son[u]=v;
    }
}

I void add(int u,int fa,int val)
{
    cnt[col[u]]+=val;
    if(mx==cnt[col[u]])sum+=LL(col[u]);
    if(mx<cnt[col[u]])sum=col[u],mx=cnt[col[u]];
    for(int i=0;i<g[u].size();i++)
    {
        int v=g[u][i];
        if(v==fa||v==Son)continue;
        add(v,u,val);
    }
}

I void dfs(int u,int fa,bool opt)//opt为是否保留答案 
{
    for(int i=0;i<g[u].size();i++)
    {
        int v=g[u][i];
        if(v==fa||v==son[u])continue;
        dfs(v,u,0);//递归处理所有轻儿子 
    }
    if(son[u])dfs(son[u],u,1),Son=son[u];
    //处理所有重儿子并得到重儿子所在子树答案 
    add(u,fa,1);//得到轻儿子所在子树的答案
    Son=0;//注意这里，如果要消除影响，重儿子的影响也要消除 
    ans[u]=sum;//得出答案 
    if(!opt)add(u,fa,-1),sum=0,mx=0;//消除影响，看情况要不要加add函数 
}

int main()
{
    n=read();
    for(int i=1;i<=n;i++)col[i]=read();
    for(int i=1;i<n;i++)
    {
        int x=read(),y=read();
        g[x].push_back(y);g[y].push_back(x);
    }
    gets(1,0);
    dfs(1,0,1);
    for(int i=1;i<=n;i++)printf("%lld ",ans[i]);
}