网络流(学习笔记)
(PS:本文纯粹复习使用,对于想看图的童鞋不是很友好)

我们想象一下自来水厂到你家的水管网是一个复杂的有向图,每一节水管都有一个最大承载流量。自来水厂不放水,你家就断水了。但是就算自来水厂拼命的往管网里面注水,你家收到的水流量也是上限(毕竟每根水管承载量有限)。你想知道你能够拿到多少水,这就是一种网络流问题。
这里,我并不喜欢直接扔一大堆定理,比如什么斜对称性啊,流量守恒啊啥啥的,当你学会网络流的基础算法之后,我相信这些都不重要。
这里我并没有按照问题的不同而分类,而是就不同的算法来考虑。
-
EK算法(Edmonds Karp算法)
——这是一个基于bfs的单路增广算法。
前置知识:
网络流里的增广路:如果存在一条路径c(s,t),使得当前的总流量增大,那么这条路径就称为增广路。
容易发现,如果网络中不存在增广路,那么就能够得到网络流的最大流量。
那么求最大流问题就转化为求增广路问题,即不断找增广路,直到找不到为止。
怎样操作呢?我们从s开始bfs,通过残量(边的总容量减去当前流量)大于0的边,每跑到一次t时,我们把改c(s,t)路径上的最小残量找出来,把这条路径灌满:即每一条边都减去这个最小残量。
这样直到我们发现不存在这样的路径为止。
那么这里出现了一个疑问:当增广一条路径的时候,你发现另一条路径已经把当前路径上的残量减少,但是从其中的一个点到t仍有可用的残量,这时你会发现,你并不能得到最优解。行吧,这里盗个图:
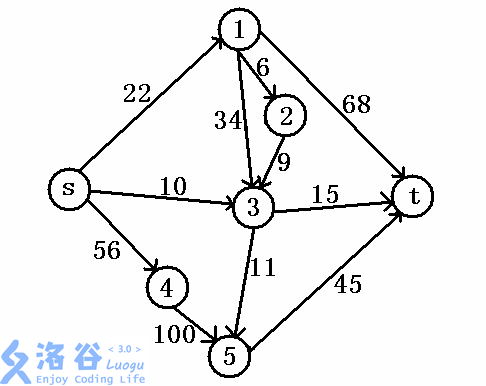
例如:你已经搜了s->3->5->t,流量是10
你又搜了s->4->5->t,减去第一条路径的流量,新增流量是35
可是你发现,你完全可以搜s->3->t和s->4->5->t,这样流量分别为10,45,显然更大。
可如果你不做任何处理的话,你会发现你在搜过s->3->5->t后,你永远不会再搜到3了,也就不会找到s->3->t这条路径了。
那么怎么办呢?我们考虑对每条边加一条初始流量为0的反向边。
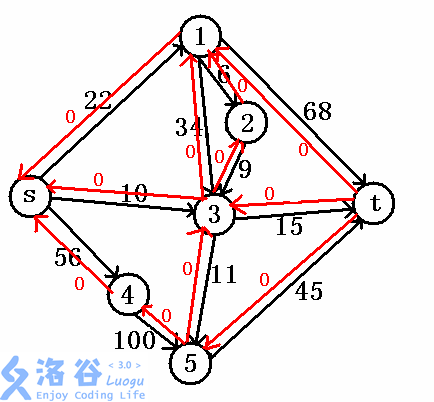
当我们先搜s->3->5->t时,我们把正边减去最大流量,反边加上最大流量。
这就告诉了第二条路径s->4->5->t,在到达节点5时,其实有10的流量是通过3留过来的,那么如果把这10流量返回去,再次从3开始跑,若能到达t则相当于找到了一条增广路。进而为第二条路径增大了10残量。
是不是很NB,下面放上code:
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<queue>
using namespace std;
const int maxn=10010;
const int maxm=100010;
const int inf=1<<30;
struct node
{
int to,next,dis;
}g[maxm*2];
int head[maxn],cnt=1;
struct P
{
int edge,from;
}pre[maxn];
int ans;
int n,m,s,t;
inline int read()
{
int x=0,f=1;
char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
return x*f;
}
inline void addedge(int u,int v,int dis)
{
g[++cnt].next=head[u];
g[cnt].to=v;
g[cnt].dis=dis;
head[u]=cnt;
}
bool vis[maxn];
bool bfs()
{
memset(vis,0,sizeof(vis));
memset(pre,-1,sizeof(pre));
queue<int>q;
q.push(s);
vis[s]=1;
while(q.size())
{
int u=q.front();q.pop();
for(int i=head[u];i;i=g[i].next)
{
int v=g[i].to;
if(!vis[v]&&g[i].dis)
{
pre[v].edge=i;
pre[v].from=u;
if(t==v)return 1;
vis[v]=1;
q.push(v);
}
}
}
return 0;
}
那么最小费用最大流呢?
其实很简单,我们只需要将bfs换成spfa就可以了。
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<queue>
using namespace std;
const int maxn=10010;
const int maxm=100010;
const int inf=1<<30;
struct node
{
int to,next,dis,val;
}g[maxm*2];
int head[maxn],cnt=1;
struct P
{
int edge,from;
}pre[maxn];
int dist[maxn];
int ans;
int n,m,s,t;
int cost;
inline int read()
{
int x=0,f=1;
char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
return x*f;
}
inline void addedge(int u,int v,int dis,int val)
{
g[++cnt].next=head[u];
g[cnt].to=v;
g[cnt].dis=dis;
g[cnt].val=val;
head[u]=cnt;
}
bool vis[maxn];
bool spfa()
{
memset(dist,0x3f,sizeof(dist));
memset(vis,0,sizeof(vis));
memset(pre,-1,sizeof(pre));
queue<int>q;
q.push(s);
vis[s]=1;
dist[s]=0;
while(q.size())
{
int u=q.front();q.pop();
vis[u]=0;
for(int i=head[u];i;i=g[i].next)
{
int v=g[i].to,w=g[i].val;
if(dist[v]>dist[u]+w&&g[i].dis)
{
dist[v]=dist[u]+w;
pre[v].edge=i;
pre[v].from=u;
if(!vis[v])
{
vis[v]=1;
q.push(v);
}
}
}
}
return dist[t]!=0x3f3f3f3f;
}
int EK()
{
int ans=0;
while(spfa())
{
int mi=inf;
for(int i=t;i!=s;i=pre[i].from)
{
mi=min(mi,g[pre[i].edge].dis);
}
for(int i=t;i!=s;i=pre[i].from)
{
g[pre[i].edge].dis-=mi;
g[pre[i].edge^1].dis+=mi;
}
ans+=mi;
cost+=mi*dist[t];
}
return ans;
}
int main()
{
n=read();m=read();s=read();t=read();
for(int i=1;i<=m;i++)
{
int x=read(),y=read(),z=read(),w=read();
addedge(x,y,z,w);addedge(y,x,0,-w);
}
printf("%d ",EK());
printf("%d",cost);
}
-
Dinic算法
Dinic算法比EK算法快多辣。它可以实现多路增广。
具体操作是:先用当前有残量的边构成的子图V',构造一个层次图。即满足dep(i)为点i到起点的边的条数,和树的深度相同,这里我习惯dep[s]=1。
为什么要这样构造呢,比如:对于路径c(s,u,x,v,t)和c(s,u,y,v,t),其中s->u,v-t的残量是确定的,那么对于u后面的分支,我们可以选择其中的一条进行增广,且这样既不会走回去,也不会对结果产生干扰(如果其中一条路径残量为0,那么下一次分层的时候,肯定不会走这一条,因为这条路径不在V'中,而是增广另一条),并且为多路增广提供基础。
这里我们使用dfs进行增广,直接上代码吧。
#include<iostream> #include<algorithm> #include<cstdio> #include<cstring> #include<queue> using namespace std; const int M=100010; const int N=10010; const int inf=0x3f3f3f3f; struct node { int next,to,w; }g[M<<1]; int head[N],cnt=1; int n,m,s,t; int ans; bool vis[N]; int dep[N]; inline int read() { int x=0,f=1; char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();} while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();} return x*f; } inline void addedge(int u,int v,int w) { g[++cnt].next=head[u]; g[cnt].to=v; g[cnt].w=w; head[u]=cnt; } bool bfs() { for(int i=1;i<=n;i++)dep[i]=inf,vis[i]=0; queue<int>q; q.push(s); dep[s]=1;vis[s]=1; while(q.size()) { int u=q.front();q.pop();vis[u]=0; for(int i=head[u];i;i=g[i].next) { int v=g[i].to; if(dep[v]>dep[u]+1&&g[i].w) { dep[v]=dep[u]+1; if(!vis[v]) vis[v]=1,q.push(v); } } } if(dep[t]!=inf)return 1; return 0; } int dfs(int u,int flow) { if(u==t)//找到增广路 { ans+=flow;//这里可以直接累加最大流 return flow;//返回当前路径上的最小残量 } int rest=flow;//当前点的残量 for(int i=head[u];i;i=g[i].next) { int v=g[i].to; if(dep[v]==dep[u]+1&&g[i].w)//必须满足层次图 { int rlow=dfs(v,min(rest,g[i].w));//从当前点开始往t增广,返回的是u->t //的最小残量 if(rlow) { g[i].w-=rlow; g[i^1].w+=rlow;//不解释 rest-=rlow;//当前点u的残量被u->t这条路径填充了rlow if(!rest)break; } } }return flow-rest; } void dinic() { while(bfs()) { dfs(s,inf); }cout<<ans; } int main() { n=read();m=read();s=read();t=read(); for(int i=1;i<=m;i++) { int x=read(),y=read(),z=read(); addedge(x,y,z);addedge(y,x,0); } dinic(); }