废话不多说,直接上题:
1585: 【例 1】Amount of Degrees
时间限制: 1000 ms 内存限制: 524288 KB
提交数: 130 通过数: 68
【题目描述】
原题来自:NEERC 2000 Central Subregional,题面详见 Ural 1057。
求给定区间 [X,Y] 中满足下列条件的整数个数:这个数恰好等于 K 个互不相等的 B 的整数次幂之和。例如,设 X=15,Y=20,K=2,B=2,则有且仅有下列三个数满足题意:
17=24+20
18=24+21
20=24+22
【输入】
第一行包含两个整数 X 和 Y,接下来两行包含整数 K 和 B。
【输出】
只包含一个整数,表示满足条件的数的个数。
【输入样例】
15 20 2 2
【输出样例】
3
【提示】
数据范围与提示:
对于全部数据,1≤X≤Y≤231−1,1≤K≤20,2≤B≤10。
【来源】
这道题一看就会先想到暴力||搜索算法,但是,它们的时间复杂度还是太高,拿不了满分。仔细一看数据规模,就会发现数据规模实在太大了,于是我们就不能设计O(n2)或更高时间复杂度的算法了,甚至O(n)都存在问题,无法满足,太血腥了,我们不得不设计一个O(log n)的算法。
但是这么快的算法绝对不可能是拿来数据直接算的,那么就要采用预处理的方法,减小时间复杂度。
在这之前,先来思考,O(log n)听着这么洋气,那么什么东西和这有关呢?对,完全二叉树的层数!没错,我们虽然不需要用到树的数据结构,但是也要在脑海中想象一棵完全二叉树。算了,不用想象了,直接上图:
先吐槽一下,一本通提高篇上的图怎么没有颜色,哪来什么蓝、绿、紫子树。
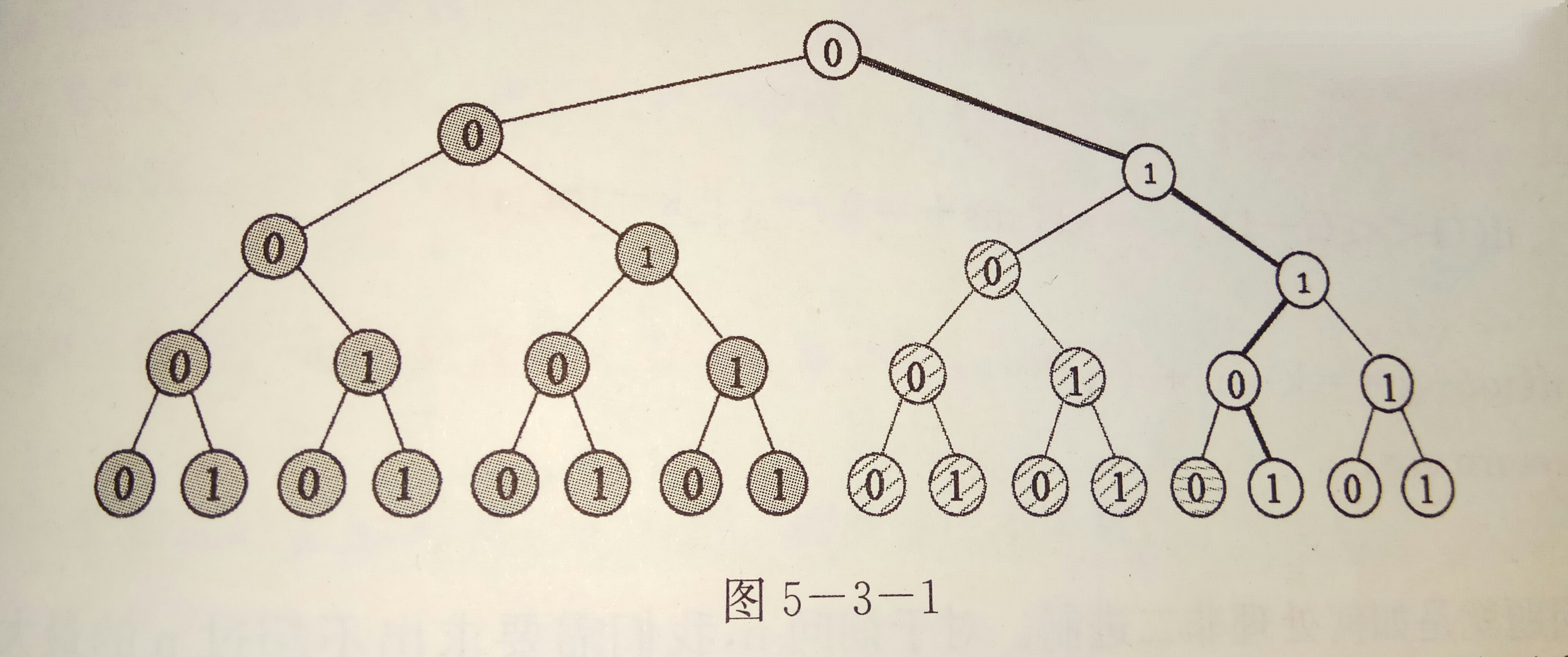
这才是正宗的图:
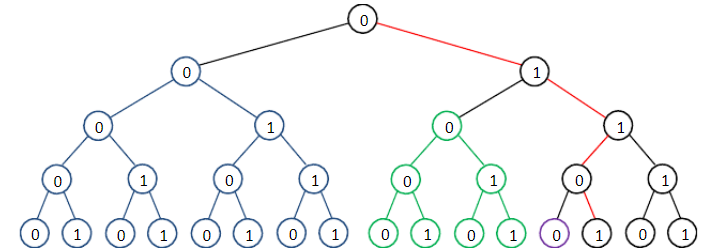
题目中只告诉了B进制,那么我们可以先假设是二进制,那么就可以画出一棵如上图所示的深度为4的完全二叉树。假设当前要求0~13区间内k=3,b=2满足要求的数的个数,13的二进制表示是1101。为了方便,根节点就为0表示;
没错,图中红线所穿过的节点正是13,那么0~13区间就分为了图中的蓝子树、绿子树、紫子树和13四个部分;细细观察就会发现每一棵带着其他颜色的子树都是13这条路径上节点的左子树。
很明显,所有满足条件的数的路径上都不多不少有3个“1”,其实1不仅是这些数二进制中的组成部分,更是这个位置上的次方选还是不选的标志,1是选,0是不选,如果不懂,可以亲手画图试试就知道了;
那么我们不妨用f[i][j]来表示深度为i的完全二叉树中选j个“1”的符合条件的数的个数。那么则有f[i][j]=f[i-1][j]+f[i-1][j-1],为什么呢?实在不好理解,那么就直接上个图吧:

这样就清晰多了,红线下的是第i层,红线上的就是第i-1层,那么我们会发现i-1层选j个的数都会和第i层的0相接,形成f[i-1][j]个满足条件的数;反之i-1层选j-1个数的都会和i层的1相接,形成f[i-1][j-1]个满足条件的数,那么f[i][j]自然就是它们的和了。
这就是预处理。
很明显,[x,y]区间内的满足条件的数的个数可以表示为[0,y]区间满足条件个数-[0,x-1]区间满足条件个数(类似于前缀和)。
那么我们在计算[0,y]区间满足条件个数和[0,x-1]区间满足条件个数时,只要一直在向右走时(这一位是1)把左子树满足条件个数记录上,最后再判断一下当前路径是否满足条件即可。
如果你看过刘聪的浅谈数位(戳这里了解),那么你一定会认为他讲的很详细。
但是结尾处有一句话:对于询问n,我们需要求出不超过n的最大B进制数,表示只含0、1的数:找到n的左起第一位非0、1的数位,将它变为1,并将它右面所有数位设成1。将得到的B进制数表示视为二进制进行询问即可。(出自刘聪的浅谈数位&信息奥赛一本通提高篇)
这句话只写作法,不写原因,使小编很长时间不能理解。
其实很好理解,比方说13,我们将它变成2进制的形式,那么就是(1101)2,也可以表示为这样的形式:13=1*23+1*22+0*21+1*20,那么对于一个数n,就可以这样表示:n = ai*ni + ai-1*ni-1 + ai-2*ni-2……所有的ai、ai-1、ai-2……不就都是0或1吗?(因为是二进制),注意审题,题中满足条件的数像这样表示,那么ai就只能是0或1,否则就不满足条件。回归正题:比方说593,变成8进制就是(1121)8,那么2就是第一个非1、0数位,那么就会把它变成(1111)8,这是为什么呢?我们会轻易的发现(1111)8到(1121)8区间内是绝对没有满足条件的数的,所以无需再找。其实说白了这个操作并不是转进制,而是1是能选,0是不选罢了,这个操作只是找到最大的区间内符合条件的数,刚好能当二进制罢了。
哎,我也是厉害了,竟然能对着这行代码耗了一中午。不说了,直接上代码,详见注释:
1 #include<iostream> 2 using namespace std; 3 int x,y,k,b,s[1000],f[1000][1000]; 4 int turn(int a,int b) 5 { 6 int cnt=0,ans=0; 7 while(a)//转成b进制 8 { 9 s[++cnt]=a%b; 10 a/=b; 11 } 12 for(int i=cnt;i>=1;i--) 13 { 14 if(s[i]>1)//找到第一个不是0、1的数位 15 { 16 for(int j=i;j>=1;j--) 17 s[j]=1;//全部改成1,这是最大的比a小的符合要求的数 18 break; 19 } 20 } 21 for(int i=1;i<=cnt;i++) if(s[i]) ans=ans|(1<<(i-1));//这是位运算,在二进制中相当于十进制的加法 22 return ans; 23 } 24 void init()//预处理 25 { 26 f[0][0]=1;//这个千万别忘了 27 for(int i=1;i<=31;i++) 28 { 29 f[i][0]=1;//因为选0个“1”所以只有0,0,0,0,0,0……这条路径可以 30 for(int j=1;j<=i;j++) f[i][j]=f[i-1][j]+f[i-1][j-1];//详见上文 31 } 32 } 33 int calc(int num,int j) 34 { 35 int cnt=0,ans=0; 36 for(int i=31;i>0;i--) 37 { 38 if((1<<i)&num)//(位运算)如果当前这一位是1 39 { 40 cnt++; 41 if(cnt>j) break;//已经多了,就不必找了 42 num=num^(1<<i);//将这一位变成0,对后面有用 43 } 44 if((1<<(i-1))<=num)//如果下一位是1 45 ans+=f[i-1][j-cnt];//加上相应的左子树的值 46 } 47 if(cnt+num==j) ans++;//如果刚好够,那么当前路径也要计入 48 return ans; 49 } 50 int main() 51 { 52 cin>>x>>y>>k>>b; 53 x=turn(x,b);y=turn(y,b); 54 init(); 55 cout<<calc(y,k)-calc(x-1,k);//前缀和 56 return 0; 57 }