▎前置基础
啥也不用说,不会动态规划绝对看不懂,请不会动态规划的同志们先戳这里了解基础动态规划。
▎什么是区间动态规划?
区间动态规划可以理解为用了分治的动态规划。
顾名思义,动态规划中涉及了区间,那么这正好和分治常用题型一样,如果你知道分治是什么,那么就很容易理解了。
那么先来想想分治是什么?分而治之,就是把一个大问题分成小问题,再把小问题的结果合并起来,就得到了原大问题的结果。
掺了分治的动态规划也可以这样,比方说现在要求f[i][j],那么我们总能找到k,使i≤k<j,分别求出f[i][k]和f[k+1][j]的值,再加起来,就是f[i][j]的值。图解一下就是这样的:

当要求的是最优值时就可以表示为f[i][j]=max{f[i][k]+f[k+1][j]},其中k是变量,依次在区间[i,j]中找到k值,计算找到最大的f[i][k]+f[k+1][j]值,就是f[i][j]的值。
你可能会问怎么知道f[i][k]和f[k+1][j]的值,很简单,要么递归,要么递推,递归的话直到递归边界会返回一个值,逐步回带;递推是一步一步算上来的,在算f[i][j]以前就先算过了f[i][k]和f[k+1][j]。
▎实战演练
可能有点难理解,主要是却例子,那么就直接上题吧!
信息奥赛一本通1570能量项链题
☞『题目』
1570:【例 2】能量项链
时间限制: 1000 ms 内存限制: 524288 KB
提交数: 279 通过数: 189
【题目描述】
原题来自:NOIP 2006
在 Mars 星球上,每个 Mars 人都随身佩带着一串能量项链。在项链上有 N 颗能量珠。能量珠是一颗有头标记和尾标记的珠子,这些标记对应着某个正整数。并且,对于相邻的两颗珠子,前一颗珠子的尾标记必定等于后一颗珠子的头标记。因为只有这样,通过吸盘——Mars 人吸收能量的器官的作用,这两颗珠子才能聚合成一颗珠子,同时释放出可被吸盘吸收的能量。如果一颗能量珠头标记为 m,尾标记为 r,后一颗能量珠头标记为 r,尾标记为 n,则聚合后释放出 m×r×n Mars单位的能量,新珠子头标记为 m,尾标记为 n。
当需要时,Mars 人就用吸盘夹住相邻的两颗珠子,通过聚合得到能量,直到项链上只剩下一颗珠子为止。显然,不同的聚合顺序得到的总能量是不一样的。请设计一个聚合顺序使得一串珠子聚合后释放出的总能量最大。
例如,设 N=4,四颗珠子头标记与尾标记分别为 (2,3),(3,5),(5,10),(10,2)。我们用记号 ⨂ 表示两颗珠子的聚合操作,(j⨂k) 表示 j,k两颗珠子聚合后释放出的能量,则4,1两颗珠子聚合后所释放的能量为(4⨂1)=10×2×3=60,这一串项链可以得到最优值的一个聚合顺序所释放出的总能量为(((4⨂1)⨂2)⨂3)=10×2×3+10×3×5+10×5×10=710
现在给你一串项链,项链上有 n 颗珠子,相邻两颗珠子可以合并成一个,合并同时会放出一定的能量,不同珠子合并放出能量不相同,请问按怎样的次序合并才能使得释放的能量最多?
【输入】
第一行一个正整数 n
第二行 n 个不超过 1000 的正整数,第 i(1≤i≤n) 个数为第 i 颗珠子的头标记,当 i≠n 时第 i 颗珠子的尾标记等于第 i+1 颗珠子的头标记,当 i=n 时第 i 颗珠子的尾标记等于第 1 颗珠子的头标记。
至于珠子的顺序,你可以这样确定:将项链放在桌面上,不要出现交叉,随机指定一颗珠子为第一颗珠子,按顺时针确定其它珠子的顺序。
【输出】
输出只有一行,一个不超过 2.1×109 的正整数,表示最优聚合顺序所释放的能量。
【输入样例】
4 2 3 5 10
【输出样例】
710
【提示】
数据范围与提示:
对于 100% 的数据,4≤n≤100。
【来源】
☞『题目分析』
这道题一看似乎用原来的动态规划不好解决,那么一看到要合并,又会用到区间,就自然而然的想到了区间动态规划。
首先就有一个问题,这是个环状问题,十分棘手,遇到这种情况,我们就应该破环成链,那么怎么样才会成链呢?很简单,只要变成两个就行了。可能没有说明白,举个例子。比如说数据是这样的:1 2 3 4 5,那么我们就改成这样1 2 3 4 5 1 2 3 4 5,似乎没有什么,请先仔细看下图:
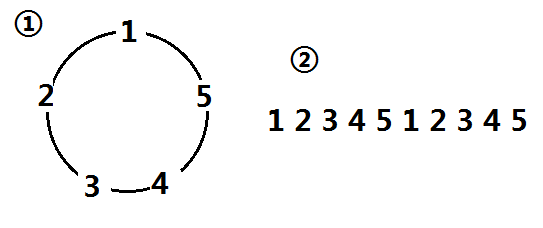
左边的环状正是以任一数作为第一个都可以。而右边呢?也可以!比如说3开头,那么请看:

细细一看,这就保留了环的性质,唯一要注意的就是操作时不要忘记这是5个数,而不是10个数。
好了,回到这道题,我们可以使用破环成链的方法使问题更简便。
那么我们如何区间动态规划呢?
首先先来思考,我们一定是先合并小的区间,一步一步地合到大区间,而不是直接上来合并大区间的,小区间还没算,大区间怎么可能算过?
所以我们肯定是先合并相邻的,再合并区间长为2的,再是3的,4的……所以,我们需要一个变量t来存储我们现在需要合并长为几的区间,同时根据这个变量t和起始位置i来确定j的位置。
这样,思路就很清晰了,详见代码注释。
☞『Code speaks louder than words!』
1 #include<iostream> 2 using namespace std; 3 int head[10000],tail[10000],f[1000][1000],num,ans; 4 inline int add(int n,int m,int r)//计算获得的能量值 5 { 6 return n*m*r; 7 } 8 int main() 9 { 10 cin>>num; 11 for(int i=1;i<=num;i++) 12 { 13 cin>>head[i]; 14 head[i+num]=head[i];//破环成链 15 } 16 for(int i=1;i<=2*num-1;i++) 17 { 18 tail[i]=head[i+1];//计录尾标记 19 } 20 tail[2*num]=head[1];//最后一个是特例,要单独赋值 21 for(int t=1;t<=num-1;t++)//合并区间的长度 22 for(int i=1;i<=2*num-t;i++)//剪t是为了避免j超出2*num 23 { 24 int j=i+t; 25 for(int k=i;k<j;k++)//i,j之间的过继点 26 { 27 f[i][j]=max(f[i][j],f[i][k]+f[k+1][j]+add(head[i],tail[k],tail[j]));//详见上文 28 } 29 } 30 for(int i=1;i<=num;i++) ans=max(ans,f[i][i+num-1]);//因为每一个点都可以是第一个,找到所有情况中的最大值 31 cout<<ans; 32 return 0; 33 }