进入图之后,最短路径可谓就是一大重点,最短路径的求法有很多种,每种算法各有各的好处,你会几种呢?下面来逐个讲解。
1 floyed算法
1)明确思想及功效:在图中求最短路还是要分开说的,分别是单源最短路和多源最短路,而floyed算法是求多源最短路的,什么是多源最短路呢?简单来说就是用完算法之后能直接写出任意两点间的最短路径长度。floyed算法在本质上是动态规划思想,不断更新最短路径的值,主要思想就是不断判断两个点是否可以通过一个点中继以刷新当前两个点最短路径的估计值,直到每两个点都判断完成。很容易理解,就不详细图解了。
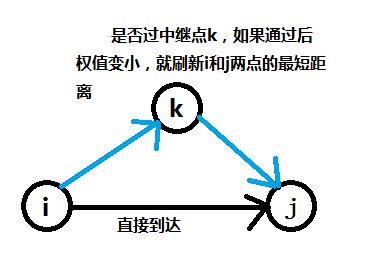
2)代码:
1 for(int k=1;k<=n;k++) 2 for(int i=1;i<=n;i++) 3 for(int j=1;j<=n;j++) 4 { 5 if(a[i][j]>a[i][k]+a[k][j]) 6 { 7 a[i][j]=a[i][k]+a[k][j]; 8 } 9 10 }
3)时间复杂度:O(n^3)
2 dijkstra算法
1)思想及其功效:dijkstra算法属于单源最短路算法,简单说就是用过之后,只能直接写出一点到其他任意一点的最短路径长度。这个算法类似于prim算法,找出刷新点所能到达的点,然后再继续刷新,写起来太难理解,自己都不会说了,那就具体以一幅图来讲解。
如果这个图是这样的:
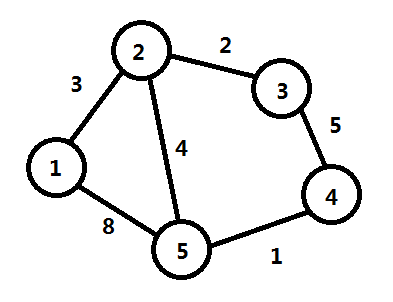
当然,图要用矩阵来存储。因为是单源最短路,只能求一个点到其他各点的最短距离,所以我们可以假设是求1号点到其他各点的最短距离。此时我们需要一个数组dis[ ]来存储1到5个顶点分别的最短路径长度。那么,在最开始时,数组里初始化为估计值,凡是1能到达的点,相应路径的长度会直接存在数组中,而不能直接到达的点则被当做正无穷,可以赋值成999999或0x3f3f3f3f等尽可能大的数,具体是什么样呢?如图所示:
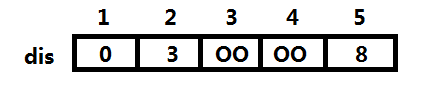
思考几个问题:
- 为什么dis[1]的值是0?
answer:因为dis[ ]数组所存的是1到各点的最短路径长度,1到1不用走,直接就到了呀,所以是0;
- OO是什么?
answer:因为画图软件不会画无限符号,就用这个代替正无穷吧,写代码时可以赋成尽可能大的值。
- 为什么有的赋值了而有的没有?
answer:如上面所说,比如2和5,从图上看它们都和1有直接连边,可以赋进dis里,但是3和4与1无直接连边,只能通过其他点间接到达,所以先赋估计值正无穷。
接着就把刚才刷新的2和5作为中继看一看是否可以刷新其他点的值。
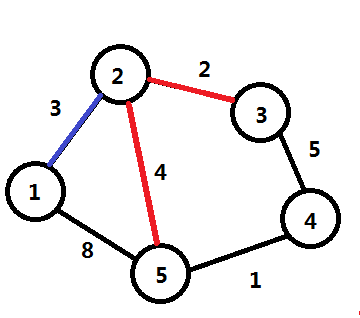

先来看一看通过2所能刷新的点,分别是3和5,dis[3]原本是正无穷,现在通过2只需要权值5就能到达,比正无穷小,就更新它,像这种操作,专业术语叫做“松弛”,同理,继续松弛操作,dis[5]的值本来为8,因为通过2来中继,3+4<8,所以更新它,继续这样操作不断循环下去,直到所有未知点全部被访问并进行松弛操作。
 //蓝边表示中继,红边代表这条边不能用,绿边表示可以通过这条边来刷新。
//蓝边表示中继,红边代表这条边不能用,绿边表示可以通过这条边来刷新。

刚才刷新了3和4,现在通过3和4来中继。
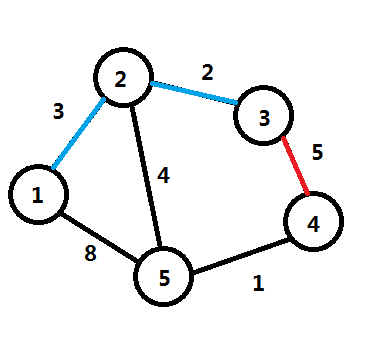
通过3无法继续刷新,继续看4。

依旧没点刷新,此时,所有点都访问过了,并进行了松弛操作所有的dis[ ]全部从估计值一步步变成了确定值。
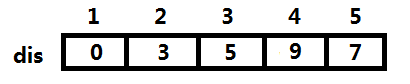
算法演示结束。
2)主要问题
- 怎么确定所有顶点被访问过?
answer:可以定义一个vis[ ]数组,最开始全是0,每选出一个点,就把vis的值更新为1。
- 先找哪个点为中继?
answer:先选一条没有访问过且dis值最小的。
- 有代码吗?
answer:有,如下:
1 void dijkstra() 2 { 3 4 vis[1]==0;dis[1]=0; 5 for(int i=1;i<=n-1;i++) 6 { 7 minn=inf; 8 for(int j=1;j<=n;j++) 9 { 10 if(vis[j]==0&&dis[j]<minn) 11 { 12 k=j; 13 minn=dis[j]; 14 } 15 } 16 vis[k]=1; 17 for(int j=1;j<=n;j++) 18 { 19 if(dis[j]>dis[k]+map[k][j]&&map[k][j]<inf) 20 dis[j]=dis[k]+map[k][j]; 21 } 22 } 23 }
3)时间复杂度:O(n^2 )
3 SPFA
图的权值有正的,当然也有负的,对于负边权,之前学过的算法都无法处理,而SPFA则能处理负权边。思路和dijkstra有点像,具体图解,想看点这里【最短路径】 SPFA算法。先放个代码凑个数:
void SPFA() { for(int i=1;i<=n;i++) dis[i]=inf; queue<int>q; q.push(1);vis[1]=1;dis[1]=0; while(q.size()) { x=q.front();q.pop();vis[x]=0; for(int i=head[x];i;i=a[i].next) { int s=a[i].to; if(dis[s]>dis[x]+a[i].cost) { dis[s]=dis[x]+a[i].cost; if(vis[s]==0) { vis[s]=1; q.push(s); } } } } }
4 例题讲解:
1376:信使(msner)
时间限制: 1000 ms 内存限制: 65536 KB
提交数: 1847 通过数: 879
【题目描述】
战争时期,前线有n个哨所,每个哨所可能会与其他若干个哨所之间有通信联系。信使负责在哨所之间传递信息,当然,这是要花费一定时间的(以天为单位)。指挥部设在第一个哨所。当指挥部下达一个命令后,指挥部就派出若干个信使向与指挥部相连的哨所送信。当一个哨所接到信后,这个哨所内的信使们也以同样的方式向其他哨所送信。直至所有n个哨所全部接到命令后,送信才算成功。因为准备充足,每个哨所内都安排了足够的信使(如果一个哨所与其他k个哨所有通信联系的话,这个哨所内至少会配备k个信使)。
现在总指挥请你编一个程序,计算出完成整个送信过程最短需要多少时间。
【输入】
第1行有两个整数n和m,中间用1个空格隔开,分别表示有n个哨所和m条通信线路,且1≤n≤100。
第2至m+1行:每行三个整数i、j、k,中间用1个空格隔开,表示第i个和第j个哨所之间存在通信线路,且这条线路要花费k天。
【输出】
一个整数,表示完成整个送信过程的最短时间。如果不是所有的哨所都能收到信,就输出-1。
【输入样例】
4 4 1 2 4 2 3 7 2 4 1 3 4 6
【输出样例】
11
这道题一看感觉没思路,就盲目的先写一遍floyed,再看看有没有什么规律,写着写着就想通了,既然每两个哨所之间都可以直接/间接的通信,而且起点是从第一个哨所开始的,那么整个时间当然就是1号哨所到达其他哨所的最短路径中最大的,应为其他路径在执行此路径时也在同时进行,废话不多说,代码如下:
//floyed 版1376:信使(msner)
1 #include<iostream>
2 using namespace std;
3 int a[1000][1000],n,m,d,b,c;int maxn=-1;
4 int main()
5 {
6 cin>>n>>m;
7 for(int i=1;i<=n;i++)
8 for(int j=1;j<=n;j++)//初始赋成尽可能大的值
9 a[i][j]=999999;
10 for(int i=1;i<=n;i++)
11 a[i][i]=0;
12 for(int i=1;i<=m;i++)
13 {
14 cin>>d>>b>>c;
15 a[d][b]=c;
16 a[b][d]=c;
17 }
18 for(int k=1;k<=n;k++)
19 for(int i=1;i<=n;i++)
20 for(int j=1;j<=n;j++)
21 {
22 if(a[i][j]>a[i][k]+a[k][j])//floyed算法
23 {
24 a[i][j]=a[i][k]+a[k][j];
25 }
26
27 }
28 for(int i=1;i<=n;i++)
29 {
30 if(maxn<a[1][i])//选出最大的路径
31 maxn=a[1][i];
32 }
33 cout<<maxn;
34 return 0;
35 }
//dijksra版1376:信使(msner)
1 #include<iostream> 2 #define inf 999999 3 using namespace std; 4 int n,m,map[1000][1000],dis[1000],vis[1000],a,b,maxn=-1,minn,k; 5 inline void dijkstra() 6 { 7 8 vis[1]==0;dis[1]=0; 9 for(int i=1;i<=n-1;i++) 10 { 11 minn=inf; 12 for(int j=1;j<=n;j++) 13 { 14 if(vis[j]==0&&dis[j]<minn) 15 { 16 k=j; 17 minn=dis[j]; 18 } 19 } 20 vis[k]=1; 21 for(int j=1;j<=n;j++) 22 { 23 if(dis[j]>dis[k]+map[k][j]&&map[k][j]<inf) 24 dis[j]=dis[k]+map[k][j]; 25 } 26 } 27 } 28 int main() 29 { 30 cin>>n>>m; 31 for(int i=1;i<=n;i++) 32 { 33 for(int j=1;j<=n;j++) 34 map[i][j]=inf; 35 dis[i]=inf; 36 } 37 for(int i=1;i<=m;i++) 38 { 39 cin>>a>>b; 40 cin>>map[a][b]; 41 map[b][a]=map[a][b]; 42 } 43 for(int i=1;i<=n;i++) 44 dis[i]=map[1][i]; 45 dijkstra(); 46 for(int i=1;i<=n;i++) 47 { 48 if(dis[i]>maxn) 49 maxn=dis[i]; 50 } 51 cout<<maxn; 52 return 0; 53 }
//SPFA版 1376:信使(msner)
1 #include<iostream> 2 #include<cstdio> 3 #include<queue> 4 #define inf 999999 5 using namespace std; 6 struct map{ 7 int from; 8 int to; 9 int cost; 10 int next; 11 }a[1000]; 12 int head[1000],dis[1000],vis[1000],n,m,maxn=-1,x,cnt,a1,b1,c1; 13 void add(int from,int to,int cost) 14 { 15 a[++cnt].to=to; 16 a[cnt].cost=cost; 17 a[cnt].next=head[from]; 18 head[from]=cnt; 19 } 20 void SPFA() 21 { 22 for(int i=1;i<=n;i++) 23 dis[i]=inf; 24 queue<int>q; 25 q.push(1);vis[1]=1;dis[1]=0; 26 while(q.size()) 27 { 28 x=q.front();q.pop();vis[x]=0; 29 for(int i=head[x];i;i=a[i].next) 30 { 31 int s=a[i].to; 32 if(dis[s]>dis[x]+a[i].cost) 33 { 34 dis[s]=dis[x]+a[i].cost; 35 if(vis[s]==0) 36 { 37 vis[s]=1; 38 q.push(s); 39 } 40 } 41 } 42 } 43 } 44 int main() 45 { 46 scanf("%d%d",&n,&m); 47 for(int i=1;i<=m;i++) 48 { 49 scanf("%d%d%d",&a1,&b1,&c1); 50 add(a1,b1,c1); 51 add(b1,a1,c1); 52 } 53 54 SPFA(); 55 for(int i=2;i<=n;i++) 56 if(dis[i]>maxn&&dis[i]!=inf) maxn=dis[i]; 57 printf("%d",maxn); 58 return 0; 59 }
//SPFA+SLF版 1376:信使(msner)
1 #include<iostream> 2 #include<cstdio> 3 #include<queue> 4 #include<cstring> 5 #define inf 0x3f3f3f3f 6 using namespace std; 7 int dis[500000],head[500000]={0},vis[500000]={0},n,m,s,x,a,b,c,cnt,maxn; 8 struct edge{ 9 int from; 10 int to; 11 int value; 12 int next; 13 }map[500000]; 14 inline void add(int from,int to,int value) 15 { 16 map[++cnt].to=to; 17 map[cnt].value=value; 18 map[cnt].next=head[from]; 19 head[from]=cnt; 20 } 21 void SPFA() 22 { 23 memset(dis,inf,sizeof(dis)); 24 deque<int>q; 25 q.push_back(1);dis[1]=0;vis[1]=1; 26 while(q.size()) 27 { 28 x=q.front();q.pop_front();vis[x]=0; 29 for(int i=head[x];i;i=map[i].next) 30 { 31 s=map[i].to; 32 if(dis[s]>dis[x]+map[i].value) 33 { 34 dis[s]=dis[x]+map[i].value; 35 if(vis[s]==0) 36 { 37 if(dis[s]<dis[q.front()]) q.push_front(s); 38 else q.push_back(s); 39 vis[s]=1; 40 } 41 } 42 } 43 } 44 } 45 int main() 46 { 47 scanf("%d%d",&n,&m); 48 for(int i=1;i<=m;i++) 49 { 50 scanf("%d%d%d",&a,&b,&c); 51 add(a,b,c); 52 add(b,a,c); 53 } 54 SPFA(); 55 for(int i=1;i<=n;i++) 56 if(dis[i]>maxn) maxn=dis[i]; 57 cout<<maxn; 58 return 0; 59 }
//SPFA+LLL版 1376:信使(msner)
1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<queue> 5 #define inf 0x3f3f3f3f 6 using namespace std; 7 int dis[500000],head[500000]={0},vis[500000]={0},n,m,sum,x,y,a,b,c,cnt,p,s,maxn=-1,cnt_2=1; 8 struct edge{ 9 int from; 10 int to; 11 int value; 12 int next; 13 }map[500000]; 14 inline void add(int from,int to,int value) 15 { 16 map[++cnt].to=to; 17 map[cnt].value=value; 18 map[cnt].next=head[from]; 19 head[from]=cnt; 20 } 21 void SPFA() 22 { 23 memset(dis,inf,sizeof(dis)); 24 queue<int>q; 25 q.push(1);dis[1]=0;vis[1]=1; 26 while(q.size()) 27 { 28 p=q.front();q.pop(); 29 if(dis[p]*cnt_2>sum) 30 { 31 q.push(p); 32 continue; 33 } 34 sum-=dis[p];cnt_2--; 35 vis[p]=0;; 36 for(int i=head[p];i;i=map[i].next) 37 { 38 s=map[i].to; 39 if(dis[s]>dis[p]+map[i].value) 40 { 41 dis[s]=dis[p]+map[i].value; 42 if(vis[s]==0) 43 { 44 vis[s]==1; 45 q.push(s); 46 cnt_2++; 47 sum+=dis[s]; 48 } 49 } 50 } 51 } 52 } 53 int main() 54 { 55 scanf("%d%d",&n,&m); 56 for(int i=1;i<=m;i++) 57 { 58 scanf("%d%d%d",&a,&b,&c); 59 add(a,b,c); 60 add(b,a,c); 61 } 62 SPFA(); 63 for(int i=1;i<=n;i++) 64 if(maxn<dis[i]) maxn=dis[i]; 65 printf("%d",maxn); 66 return 0; 67 }
//SPFA+SLF+LLL版 1376:信使(msner)
#include<iostream> #include<cstdio> #include<cstring> #include<queue> #define inf 0x3f3f3f3f using namespace std; int dis[500000],head[500000]={0},vis[500000]={0},n,m,sum,x,y,a,b,c,cnt,p,s,maxn=-1,cnt_2=1; struct edge{ int from; int to; int value; int next; }map[500000]; inline void add(int from,int to,int value) { map[++cnt].to=to; map[cnt].value=value; map[cnt].next=head[from]; head[from]=cnt; } void SPFA() { memset(dis,inf,sizeof(dis)); deque<int>q; q.push_back(1);dis[1]=0;vis[1]=1; while(q.size()) { p=q.front();q.pop_front(); if(dis[p]*cnt_2>sum) { q.push_back(p); continue; } sum-=dis[p];cnt_2--; vis[p]=0;; for(int i=head[p];i;i=map[i].next) { s=map[i].to; if(dis[s]>dis[p]+map[i].value) { dis[s]=dis[p]+map[i].value; if(vis[s]==0) { vis[s]==1; if(dis[s]<dis[q.front()]) q.push_front(s); else q.push_back(s); cnt_2++; sum+=dis[s]; } } } } } int main() { scanf("%d%d",&n,&m); for(int i=1;i<=m;i++) { scanf("%d%d%d",&a,&b,&c); add(a,b,c); add(b,a,c); } SPFA(); for(int i=1;i<=n;i++) if(maxn<dis[i]) maxn=dis[i]; printf("%d",maxn); return 0; }
写是确实写了六次,看看你会写几种?但是想着应该是越往后越快呀,后面有用到优化,可是结果堪忧啊。
 //SPFA三种优化方法
//SPFA三种优化方法
 //SPFA、dijkstra、floyed
//SPFA、dijkstra、floyed
天哪!合着我这是优化的越来越慢了,看来优化也得慎重啊。下一期将会重点讲述如何优化SPFA。