在上一期时间复杂度优化的文章中就已经提到过了快速幂,这一期就来讲一讲快速幂。
什么是快速幂?
快速幂正如其名,就是快速的幂,“快速”是指这种方法运算速度很快,“幂”就不用说了,(a的b次方的结果,也就是b个a相乘),一提起幂,大家一定会不约而同的想到#include<cmath>这个头文件和pow函数,但是如果不让你用这个函数,你会不会就只能写成这个德行。代码如下:
1 #include<iostream> 2 using namespace std; 3 int sxpow(int a,int b) 4 { 5 int ans=1; 6 for(int i=1;i<=b;i++) 7 ans*=a; 8 } 9 int main() 10 { 11 //do something 12 return 0; 13 }
如果你只会写成这样,那么你就out了,这样一来时间复杂度会很高,既然你诚心的进来看快速幂,就表示你现在一定会缺方法来降低时间复杂度,为了优化程序,就得来学一学快速幂了。
二进制&快速幂
说起快速幂,就得先提一下二进制,怎么也得先会二进制吧,if(你会二进制) then 继续看;else 请圆润的走开,去学二进制。不知道为什么,网上众多大牛写的博客都喜欢用11来举例,那我也用11来举例好了。假如要求一个数a的11次方,那么就先把11改写成二进制1011,也就是11=8+2+1,这样一来,根据同底数幂相乘,底数不变,指数相加,就把pow(a,11转化成pow(a,8)*pow(a,2)*pow(a,1),只需要算三次,原来要算十一次,但是pow(a,8)也不好求啊,那就用分治pow(a,8)=pow(a,4)*pow(a,4),那么pow(a,4)=pow(a,2)*pow(a,2),知道分成pow(a,1)难道pow(a,1)你求不出来吗?我想你心中一定早就有了答案,代码胜于雄辩,先看一看代码再继续解释:
1 long long quickpow(int a,int b,int mod) 2 { 3 long long ans=1,base=a; 4 while(b!=0) 5 { 6 if(b&1==1) 7 { 8 ans*=base; 9 ans%=mod; 10 } 11 base*=base; 12 base%=mod; 13 b>>=1; 14 } 15 return ans; 16 }
这就是快速幂,就像刚才说的一样,有些地方你可能会看不懂,其中b&1表示b为奇数,这是根据二进制来判断的,就比如11,二进制是1011,1的二进制是1,1011和1在第一位上相同,其他位1连数字都没有,所以11&1的值为1,表示11是奇数;除此之外还有b>>=1相当于b/=2,这么写是为了快,使用位运算;一般情况下,题中会告你一个取模值,因为幂算出来有时会很大,说不定会爆内存。
实战演练
随便看两道题,T1:

这道题看看就好,会了快速幂也不一定能做对,毕竟不是模板题,先说道简单题再看这道题。
T2:
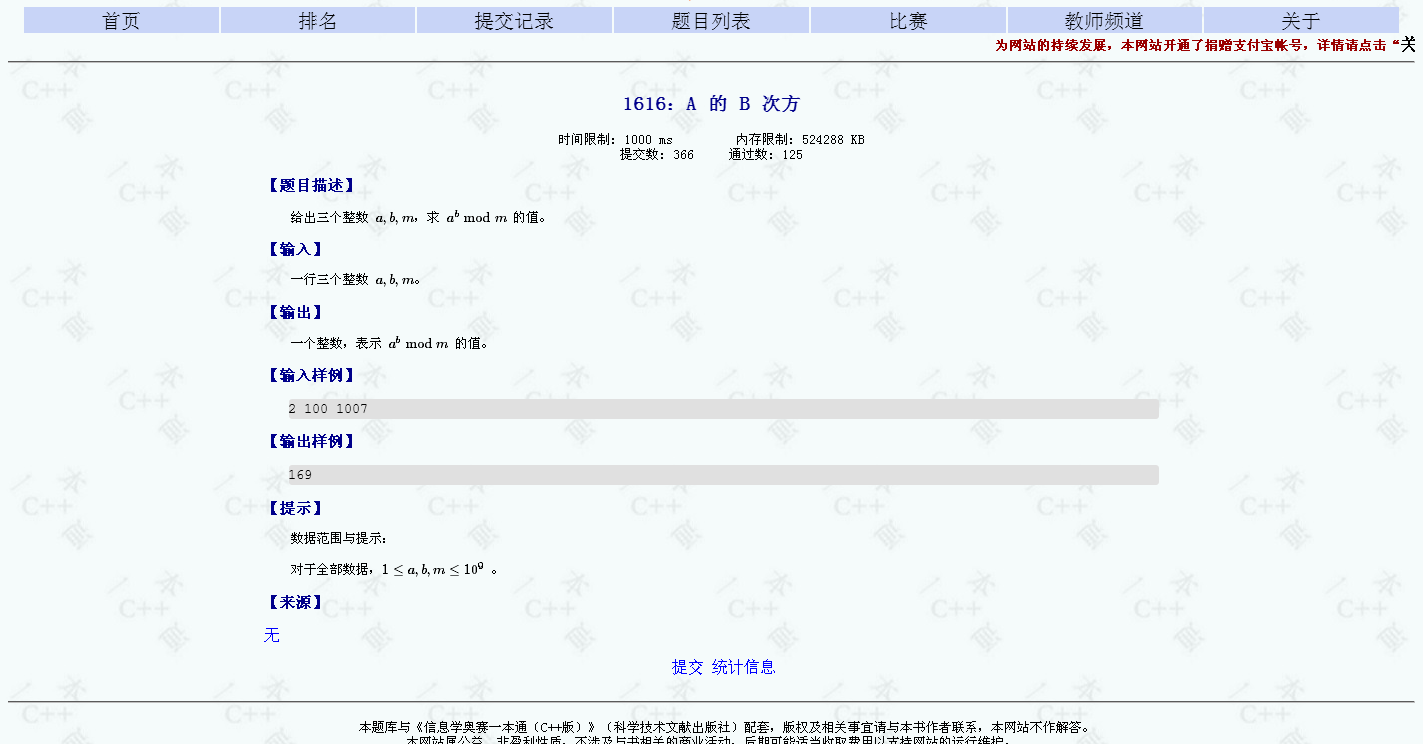
这道题有够简单的,完全没有任何变化,套进去就可以了,推荐大家可以先写这道题加深理解,AC代码如下:
1 #include<iostream> 2 using namespace std;int mod; 3 long long quickpow(int a,int b,int mod) 4 { 5 long long ans=1,base=a; 6 while(b!=0) 7 { 8 if(b&1==1) 9 { 10 ans*=base; 11 ans%=mod; 12 } 13 base*=base; 14 base%=mod; 15 b>>=1; 16 } 17 return ans; 18 } 19 int main() 20 { 21 int a,b; 22 cin>>a>>b>>mod; 23 cout<<quickpow(a,b,mod); 24 return 0; 25 }
不知道你练得如何了,(附上测评网站A的B次方)现在来回过头看T1,这道题提到的序列有两种,分别是等差序列和等比序列,这样的序列在小学就学过了吧,怎么判断是否是等差序列呢,当然好办,依据等差序列差值相等,只要判断b-a和c-b是否相等即可,如果这是一个等差序列,怎么求第k个数?当然不能一次又一次循环叫上差值,小编当初就是这么写的,后来发现好像有点麻烦,于是改成了a+(k-1)*sub&200907,看起来很简单。当然还是等比数列比较麻烦,暴力当然没辙,代码如下:
1 #include<iostream> 2 using namespace std; 3 long long a,b,c,k,T,ans;double sub; 4 int main() 5 { 6 cin>>T; 7 for(int i=1;i<=T;i++) 8 { 9 cin>>a>>b>>c>>k; 10 if(b-a==c-b) 11 { 12 sub=b-a; 13 for(int i=1;i<k;i++) 14 { 15 a+=sub; 16 if(a>200907) 17 a%=200907; 18 } 19 cout<<a<<endl; 20 } 21 else 22 { 23 sub=b*1.0/a; 24 for(int i=1;i<k;i++) 25 { 26 a*=sub; 27 if(a>200907) a%=200907; 28 } 29 cout<<a<<endl; 30 } 31 } 32 return 0; 33 }
在这拼时间的题里,怎么可能用暴力过呢?当然学来的不能丢,要转化成快速幂,仿照等差数列,那么等比数列第k个数为a*pow(sub,k-1)%200907,这么算就会快很多,AC代码如下:
#include<iostream> #include<cstdio> using namespace std; long long ans,sub,a,b,c,k,T,base; int main() { scanf("%d",&T); for(int i=1;i<=T;i++) { scanf("%d%d%d%d",&a,&b,&c,&k); if(b-a==c-b) { sub=b-a;sub%=200907; printf("%d ",(a+(k-1)*sub%200907)%200907); } else { sub=b/a;k-=1; ans=1;base=sub; while(k!=0) { if(k&1==1) { ans*=base; ans%=200907; } base*=base; base%=200907; k>>=1; } printf("%d ",a*ans%200907); } } return 0; }
//PS:为了不必要的麻烦,换成了scanf和printf,并且把快速幂写在了main函数里,以优化程序