必备知识点
-
邻接表存图
-
线段树
相关定义
-
重儿子:一个节点所有子节点中以其为根的子树的节点最多的节点
-
重边:一个节点到其重儿子的边
-
重链:一条全部由重边构成的路径(特别地,一个节点也当做一条重链)
-
轻儿子:一个节点除重儿子外的所有子节点
-
轻边:一个节点到其轻儿子的边
节点信息
-
$fa[x]$:$x$的父亲节点
-
$dep[x]$:$x$的深度
-
$siz[x]$:以$x$的子树的节点数
-
$son[x]$:$x$的重儿子
-
$top[x]$:$x$所在重链的顶部节点(即深度最小的节点)
-
$seg[x]$:$x$在线段树中的节点编号
-
$rev[x]$:线段树中编号为$x$的节点在原树中对应的节点编号
性质
-
若(x,y)为轻边,则$siz(y)leq siz(x)/2$。
证明:显然,若$siz(y)>siz(x)/2$,以y为根的子树的节点个数一定是x的儿子中最多的,与$(x,y)$是轻边,即y是轻儿子矛盾。因此$siz(y)leq siz(x)/2$。
-
从根节点到树上任意一点的路径上的轻边数不超过$logn$。
证明:由上一性质可知,从根节点向下走,每经过一条轻边,以到达的节点为根的子树的节点个数至少比以上一个节点为根的子树减少一半,因此从根节点到树上任意一点的路径上的轻边数不超过$O(logn)$。
-
从根节点到树上任意一点的路径上的重链数不超过$logn$。
证明:由上一性质可以,从根节点到树上任意一点的路径上的轻边数不超过$logn$。显然每一条重链的两端都是轻边,因此从根节点到树上任意一点的路径上的重链数不超过$logn$。
由以上性质可以看出,树链剖分可以以优秀的复杂度维护树上路径信息。
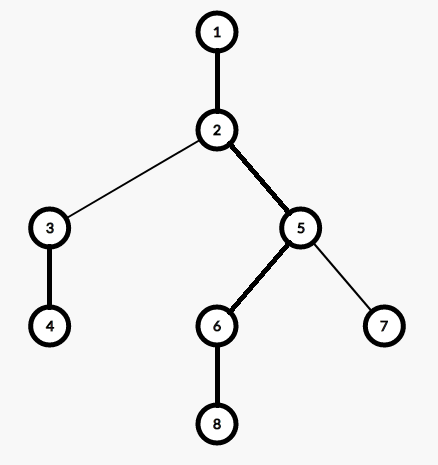
如图,加粗的就是重边。
树链剖分的实现步骤:
预处理
dfs1
第一遍dfs处理出四个的节点信息:$fa,siz,dep,son$
函数实现:
1. 处理$fa,dep$,初始化$siz$
2. 遍历当前节点的所有子节点,递归子节点
3. 回溯时累加更新$siz$,同时找到$siz$最大的子节点作为$son$
void dfs1(int u,int f)
{
siz[u]=1,fa[u]=f,dep[u]=dep[f]+1;//处理fa,dep,初始化siz
for(int i=head[u];i;i=Next[i])
{
int y=ver[i];
if(y!=f)
{
dfs1(y,u);//递归子节点
siz[u]+=siz[y];//累加更新siz
if(siz[y]>siz[son[u]])
son[u]=y;//找到siz最大的子节点
}
}
}
dfs2
第二遍dfs处理出三个节点信息:$seg,top,rev$
函数实现:
1. 若当前节点有重儿子,则先处理重儿子,保证一条重链上的节点在线段树中是连续的
2. 遍历当前节点的子节点,处理$seg,top,rev$,递归子节点
void dfs2(int u,int f)
{
if(son[u])
{
seg[son[u]]=++seg[0];//seg[0]相当于一个计量数
top[son[u]]=top[u];//显然重儿子和当前节点在同一条重链上,因此top相同
rev[seg[0]]=son[u];//根据定义即可推出
dfs2(son[u],u);//递归重儿子
}//先处理重儿子
for(int i=head[u];i;i=Next[i])
{
int y=ver[i];
if(!top[y])//若没有处理过,即轻儿子
{
seg[y]=++seg[0];
rev[seg[0]]=y;
top[y]=y;//显然轻儿子起始单独构成一条重链
dfs2(y,u);//递归子节点
}
}
}
可以注意到在这个函数里根节点是无法得到赋值的,因此要在主函数里先对根节点赋值再执行此函数。
维护树上路径信息
以洛谷模板题为例,下面实现以下四个操作:
将树从$x$到$y$结点最短路径上所有节点的值都加上$z$
模拟$x$和$y$向上走,走的同时维护路径信息,直到$x$和$y$在同一条重链上为止。
函数实现:
1. 令$x$为$x,y$中所在重链顶端节点深度较大的节点,如果不是,则交换
2. 执行区间修改操作,将$top[x]$和$x$间的所有节点加上$z$,注意,因为是从上至下递归,所以$seg[top[x]]leq seg[x]$
3. 将$x$赋值为$fa[top[x]]$,相当于模拟$x$走过当前的一整条重链到达上一条重链的底端
4. 不断执行$1-3$步,直到$x$和$y$在同一条重链上为止
5. 此时再令$x$为$x,y$中深度较小的节点,此时$seg[x]leq seg[y]$,将$x$和$y$间的所有节点加上$z$
void op1(int x,int y,int z)
{
while(top[x]!=top[y])
{
if(dep[top[x]]<dep[top[y]])
swap(x,y);//令x为x,y中所在重链顶端节点深度较大的节点
Add(1,seg[top[x]],seg[x],z);//区间修改
x=fa[top[x]];//模拟上行
}
if(dep[x]>dep[y])
swap(x,y);//令x为x,y中深度较小的节点
Add(1,seg[x],seg[y],z);//区间修改
}
求树从$x$到$y$结点最短路径上所有节点的值之和
与上一个操作类似,模拟$x,y$上行,同时对走过的区间查询,直到$x,y$在同一条重链上位置,这里就不再赘述了。
int op2(int x,int y)
{
int ans=0;
while(top[x]!=top[y])
{
if(dep[top[x]]<dep[top[y]])
swap(x,y);
ans=(ans+ask(1,seg[top[x]],seg[x]))%P;//区间查询
x=fa[top[x]];
}
if(dep[x]>dep[y])
swap(x,y);
ans=(ans+ask(1,seg[x],seg[y]))%P;
return ans;
}
将以$x$为根节点的子树内所有节点值都加上$z$
回顾$dfs2$的操作,因为是递归赋值的,因此一棵子树内的所有节点在线段树中的编号一定是连续的,因为是将所有节点都加上同一个值,因此与编号在子树内的具体顺序无关。而子树大小已经处理出来了,即$siz[x]$,因此以$x$为根的子树所有节点在线段树内的编号即为$seg[x]$~$seg[x]+siz[x]-1$,直接执行区间修改操作即可。
void op3(int x,int y)
{
Add(1,seg[x],seg[x]+siz[x]-1,y);//区间修改
}
将以$x$为根节点的子树内所有节点值都加上$z$
与上一个操作道理相同,直接执行区间查询操作即可,这里就不再赘述了。
int op4(int x)
{
return ask(1,seg[x],seg[x]+siz[x]-1);//区间查询
}
完整代码:(以线段树为例)
#include<iostream>
#include<cstdio>
using namespace std;
const int N=2e5+100;
int n,m,R,P,tot,cx,cy,X,a,b,c;
int head[N],ver[N],Next[N];
int l[N<<1],r[N<<1],rev[N<<1],sum[N<<1],add[N<<1];
int fa[N],son[N],siz[N],dep[N],top[N],seg[N];
int cn[N];
void ADD(int x,int y)
{
ver[++tot]=y,Next[tot]=head[x],head[x]=tot;
}//邻接表插入操作
void dfs1(int u,int f)
{
siz[u]=1,fa[u]=f,dep[u]=dep[f]+1;
for(int i=head[u];i;i=Next[i])
{
int y=ver[i];
if(y!=f)
{
dfs1(y,u);
siz[u]+=siz[y];
if(siz[y]>siz[son[u]])
son[u]=y;
}
}
}
void dfs2(int u,int f)
{
if(son[u])
{
seg[son[u]]=++seg[0];
top[son[u]]=top[u];
rev[seg[0]]=son[u];
dfs2(son[u],u);
}
for(int i=head[u];i;i=Next[i])
{
int y=ver[i];
if(!top[y])
{
seg[y]=++seg[0];
rev[seg[0]]=y;
top[y]=y;
dfs2(y,u);
}
}
}//树剖预处理
void build(int p,int lx,int rx)
{
l[p]=lx,r[p]=rx;
if(lx==rx)
{
sum[p]=cn[rev[lx]];
return ;
}
int mid=(l[p]+r[p])>>1;
build(p<<1,lx,mid);
build(p<<1|1,mid+1,rx);
sum[p]=(sum[p<<1]+sum[p<<1|1])%P;
}//线段树建树
void spread(int p)
{
sum[p<<1]=(sum[p<<1]+add[p]*(r[p<<1]-l[p<<1]+1))%P;
sum[p<<1|1]=(sum[p<<1|1]+add[p]*(r[p<<1|1]-l[p<<1|1]+1))%P;
add[p<<1]=(add[p<<1]+add[p])%P;
add[p<<1|1]=(add[p<<1|1]+add[p])%P;
add[p]=0;
}//线段树延迟标记
void Add(int p,int lx,int rx,int d)
{
if(lx<=l[p] && rx>=r[p])
{
sum[p]+=d*(r[p]-l[p]+1);
add[p]+=d;
return ;
}
if(add[p])
spread(p);
int mid=(l[p]+r[p])>>1;
if(lx<=mid)
Add(p<<1,lx,rx,d);
if(rx>mid)
Add(p<<1|1,lx,rx,d);
sum[p]=(sum[p<<1]+sum[p<<1|1])%P;
}//线段树区间修改
int ask(int p,int lx,int rx)
{
if(lx<=l[p] && rx>=r[p])
return sum[p];
if(add[p])
spread(p);
int mid=(l[p]+r[p])>>1;
int val=0;
if(lx<=mid)
val=(val+ask(p<<1,lx,rx))%P;
if(rx>mid)
val=(val+ask(p<<1|1,lx,rx))%P;
return val;
}//线段树区间求和
void op1(int x,int y,int z)
{
while(top[x]!=top[y])
{
if(dep[top[x]]<dep[top[y]])
swap(x,y);
Add(1,seg[top[x]],seg[x],z);
x=fa[top[x]];
}
if(dep[x]>dep[y])
swap(x,y);
Add(1,seg[x],seg[y],z);
}//树剖树上路径修改
int op2(int x,int y)
{
int ans=0;
while(top[x]!=top[y])
{
if(dep[top[x]]<dep[top[y]])
swap(x,y);
ans=(ans+ask(1,seg[top[x]],seg[x]))%P;
x=fa[top[x]];
}
if(dep[x]>dep[y])
swap(x,y);
ans=(ans+ask(1,seg[x],seg[y]))%P;
return ans;
}//树剖树上路径求和
void op3(int x,int y)
{
Add(1,seg[x],seg[x]+siz[x]-1,y);
}//树剖子树修改
int op4(int x)
{
return ask(1,seg[x],seg[x]+siz[x]-1);
}//树剖子树求和
int main()
{
scanf("%d%d%d%d",&n,&m,&R,&P);
for(int i=1;i<=n;i++)
scanf("%d",&cn[i]);
for(int i=1;i<n;i++)
{
scanf("%d%d",&cx,&cy);
ADD(cx,cy),ADD(cy,cx);
}//输入,存图
seg[R]=++seg[0];
top[R]=R;
rev[seg[R]]=R;//对根节点赋值
dfs1(R,0);
dfs2(R,0);//初始化
build(1,1,n);//建树
while(m--)
{
scanf("%d",&X);
if(X==1)
{
scanf("%d%d%d",&a,&b,&c);
op1(a,b,c%P);
}
if(X==2)
{
scanf("%d%d",&a,&b);
printf("%d
",op2(a,b));
}
if(X==3)
{
scanf("%d%d",&a,&b);
op3(a,b%P);
}
if(X==4)
{
scanf("%d",&a);
printf("%d
",op4(a));
}
}
return 0;
}
习题:
-
模板题:P3384
参考资料:
-
《信息学奥赛一本通·提高篇》
-
《算法竞赛进阶指南》
2019.8.15 于厦门外国语学校石狮分校