学习转载:原文:https://blog.csdn.net/juanjuan1314/article/details/78189527(老笨妞 阅读数:4597)
本文要总结的是3种估计的原理、估计与目标函数之间的关系。这三种估计放在一起让我晕头转向了好久,看知乎,看教材,有了以下理解。以下全部是个人看书后的理解,如有理解错误的地方,请指正,吾将感激不尽。
来自教材《深度学习》5.4-5.6…
关于频率派和贝叶斯派:频率派认为估计的模型是固定的,只是参数θ未知,而数据集样本是随机变量。
个人理解,意思是生成真实数据集的概率分布只有一个,只是我们暂时只能得到从这个分布中抽取的具体数据,而不知道这个分布是什么样的分布。认为从分布中抽取数据是随机的,因此,将数据样本看作随机变量,用这些随机变量来估计一个最佳最接近真实分布的参数,参数是数据的函数,并把这个模型分布当成真实分布来预测后续随机变量的概率。
而贝叶斯派认为,数据集能被直接观测到,那么它是确定的,不确定的反而是参数,通过确定的样本来估计参数的条件概率分布,换言之,参数是数据的条件概率分布。同时,很重要的一点:贝叶斯估计引入先验概率,先验概率是抽样前有关统计推断问题的信息。
最大似然估计(MLE)是频率派的代表,贝叶斯估计(Bayes)是贝叶斯派的代表,最大后验估计是频率派和贝叶斯派的合成。
MLE是点估计,而Bayes是概率估计。
来自知乎最赞的一个回答…
还是有点懵,再理一理公式吧…
1. 最大似然估计(MLE)
最大似然估计的定义 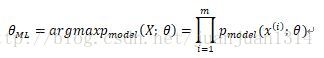
这里需要说明一下,将数据集中的各数据看做是相互独立的,因此,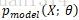
由于多个概率相乘,结果越来越小,很容易被计算设备四舍五入为0,同时,对数是单调递增的,因此,用对数累加作最大似然估计效果一样 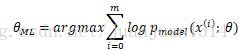
根据分布函数的期望定义: 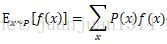
对似然函数除m后,就可以看作是所有x的权重都为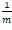
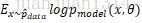
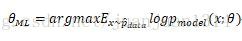
最大似然估计可以看作是把所有参数的出现概率是相等的估计。
实际应用中,估计通常是条件概率,如同分类学习算法中的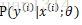
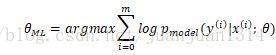
另外,根据 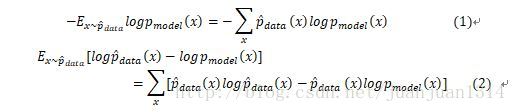
式(1)是模型的负对数似然,由于式(2)的第一项是生成分布,是固定的,最小化式(1)和最小化式(2)的效果是一样的。因此,任何一个负对数似然代价函数,与定义在训练集的经验分布和定义在模型的概率分布之间的交叉熵是等同的。
线性模型中的均方代价函数可以等同于经验分布和高斯模型之间的交叉熵。
2. 贝叶斯估计
贝叶斯统计的重点参数未知且不确定,因此作为随机变量,参数本身也是一个分布,同时,根据已有的信息可以得到参数θ的先验概率,根据先验概率来推断θ的后验概率。
根据贝叶斯规则: 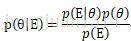
其中,p(θ)是θ的先验概率,E是观察到的现象。p(θ│E)表示根据观察到的现象估计的参数概率分布,而p(E│θ)是当前参数条件下,现象E出现的概率分布。
和最大似然估计一样,预测中观察到最直接的现象通常是结果(Y),间接一些的是原因(X),因此,
和最大似然估计不同,最大似然估计的模型是固定的,求得使似然函数最大的参数集后,模型就确定下来,就完全可以根据模型和数据预测结果了。但是,贝叶斯估计除了模型需要确定,还需要给定一个先验分布的初始模型,通常需要选择一个常用分布,并确定一个初始参数集作为先验分布。然后得到参数的后验概率分布
3.MLE和Bayes估计线性回归参数
用这两种估计的前提是将样本的模型定为多维高斯分布,高斯分布的协方差定为单位矩阵I,要通过确定参数预测均值。
线性回归的基本表达: 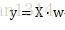
高斯分布: 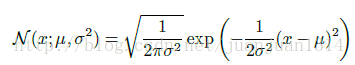
模型定为 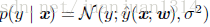
用MLE预测,其对数似然函数: 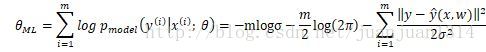
等式前两项都与w无关,只有最后一项相关,而最后一项等同于均方代价函数。因此,前面提到,线性模型的均方代价函数实际上是经验分布和高斯模型的交叉熵。
用Bayes估计:
参数w的先验分布初始化为高斯分布,均值为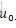
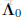
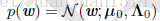
从前面推断最大似然估计中可以看出,高斯分布的对数似然函数与均方差代价函数相关,因此,p(w)的似然函数 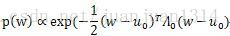
后验分布可以表示为: 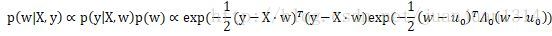
这个等式在《深度学习》5.6节中做如下化简: 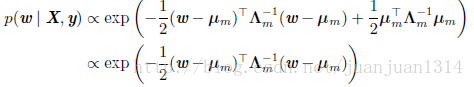
其中, 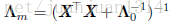
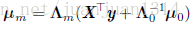
到了这里,还是不太确定,参数的后验分布确定后,在训练过程中是作为下一次学习的先验分布呢,还是用后验概率通过贝叶斯规则计算下一次学习的p(y|X,w)?如果两者都不是,那实在不能理解后验概率的作用了。个人以为第二种的可能性更大。关于这一点,暂时没有搜索到满意的答案,很多关于贝叶斯估计的博客在讲解贝叶斯估计的时候都是用贝叶斯规则来解锁贝叶斯估计的,说到的点都是先验概率,个人觉得贝叶斯估计和类似于朴素贝叶斯这种贝叶斯规则的应用还是有差别的。
4. 最大后验估计(MAP)
MAP是点估计和分布估计的结合。为什么需要这要的结合呢?虽然大家说“世界是贝叶斯的”,贝叶斯估计更合理,各参数集合的可能是相同的确实有点武断,过于简化了。但从上面用MLE和bayes估计线性回归的参数可以看到,纯正的bayes估计实际上比较麻烦哦,既要确定模型,还要事先初始化一个先验概率,估计过程涉及到两个分布的运算,最主要的是,参数估计是一个分布,对于稍微复杂的学习过程,计算就更麻烦了。
实际上,当取估计到的参数分布概率最大的点作为最佳参数,那么分布估计也就变成了点估计。取bayes估计中参数后验分布中概率最大的点来估计参数就是最大后验估计: 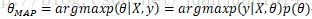
依然对这个似然函数求对数,对数函数是单调的,对最大估计无影响: 
等式最右边第一项是标准的对数似然函数,第二项是先验分布的对数。依然带入先验分布,但后验估计不再是一个全分布计算了,而是转化为对数似然计算,计算化简了很多。对数先验项本身不需要做最大估计,它如同一个惩罚项。