PHP 归并排序(接上一篇)

1、原理
归并排序是一种概念上最简单的排序算法，与快速排序一样，归并排序也是基于分治法的。归并排序将待排序的元素序列分成两个长度相等的子序列，为每一个子序列排序，然后再将他们合并成一个子序列。合并两个子序列的过程也就是两路归并。

2、复杂度
归并排序是一种稳定的排序算法，归并排序的主要问题在于它需要一个与待排序数组一样大的辅助数组空间。由于归并排序每次划分时两个子序列的长度基本一样，所以归并排序最好、最差和平均时间复杂度都是nlog2n。
通过下图非常容易看懂归并排序的过程：

//递归拆分，直到剩下一个元素，我们认为他是有序的
function fen(&$arr, $start, $end)
{
    if ($start < $end) {
        $mid = floor(($start + $end) / 2);
        fen($arr,$start,$mid);
        fen($arr,$mid+1,$end);
        //拆分完以后需要两两合并
        merge($arr,$start,$mid,$end);
    }
}

function merge(&$arr,$start,$mid,$end){
    $i = $start;
    $j = $mid+1;
    $tmp = [];
    //两两循环比较，当左边的第一个元素小于右边的第一个元素，将左边第一个元素放入临时数组
    //然后拿左边数组的第二个元素与右边数组的第一个元素比较，如果左边第二个元素大于右边第一个元素，将右边第一个放入临时数组
    //依次比较，知道有一边的元素取完为止
    while($i<=$mid && $j<=$end){
        if($arr[$i] <= $arr[$j]){
            $tmp[] = $arr[$i++];
        }else{
            $tmp[] = $arr[$j++];
        }
    }
    //将左边剩余的元素放入临时数组
    while($i<=$mid){
        $tmp[] = $arr[$i++];
    }
    //将右边剩余的元素放入临时数组
    while($j<=$end){
        $tmp[] = $arr[$j++];
    }
    //因为前面操作的都是临时数组，而归并操作的事原数组，所以还要把临时数组中的元素放入原数组中
    for($k = 0;$k<count($tmp);$k++){
        $arr[$k+$start] = $tmp[$k];
    }
}

测试：

$args = [15, 20, 3, 8, 55, 6, 88, 33, 21, 19, 36, 56, 77];

$start = 0;
$end = count($args) - 1;
fen($args,$start,$end);
echo "<pre>";
print_r($args);

输出结果为：

参考原文：https://blog.csdn.net/qq_36442947/article/details/81612870 

基本思想

　　归并排序（MERGE-SORT）是利用归并的思想实现的排序方法，该算法采用经典的分治（divide-and-conquer）策略（分治法将问题分(divide)成一些小的问题然后递归求解，而治(conquer)的阶段则将分的阶段得到的各答案"修补"在一起，即分而治之)。

分而治之

 　　可以看到这种结构很像一棵完全二叉树，本文的归并排序我们采用递归去实现（也可采用迭代的方式去实现）。分阶段可以理解为就是递归拆分子序列的过程，递归深度为log₂n。

合并相邻有序子序列

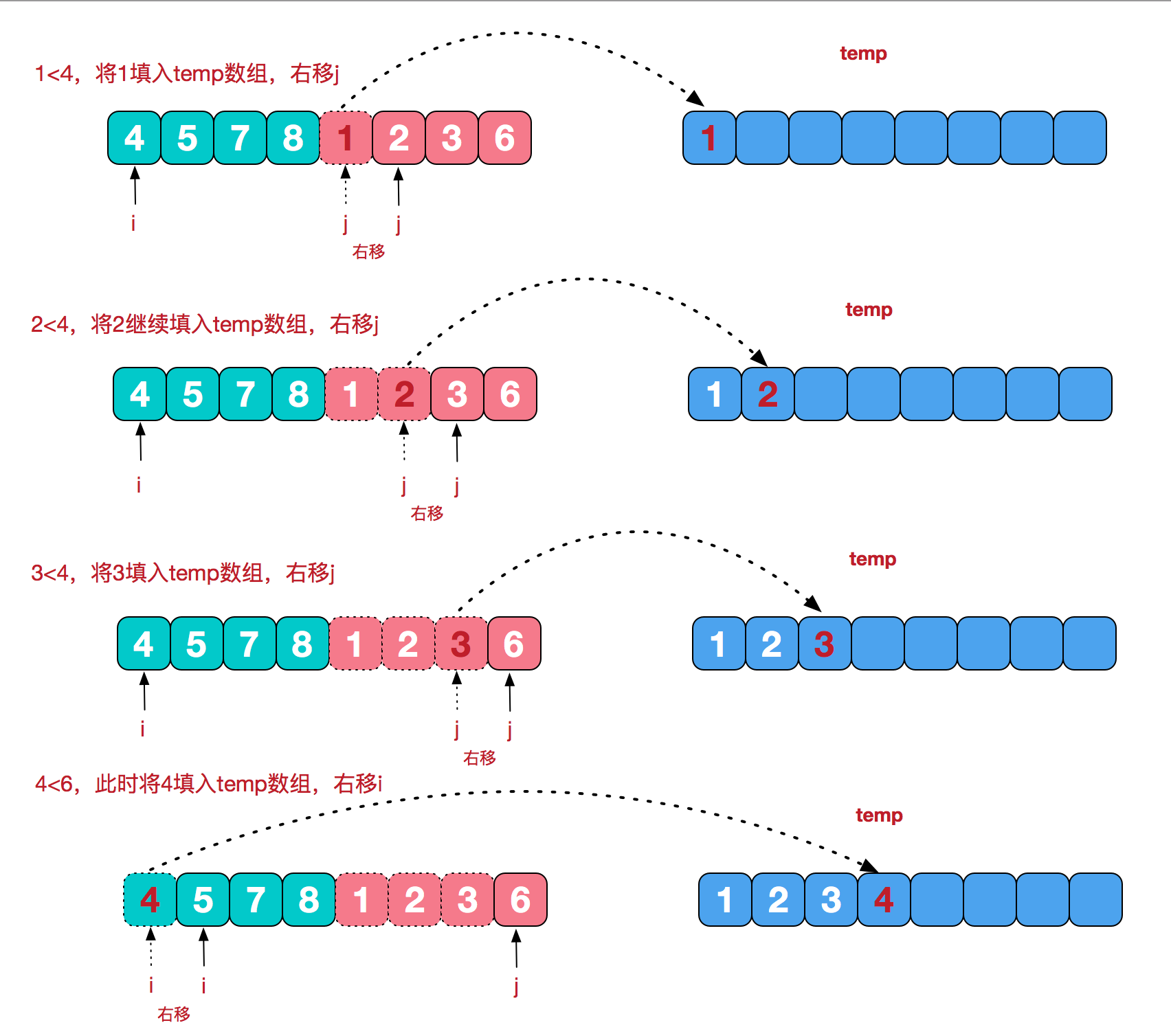
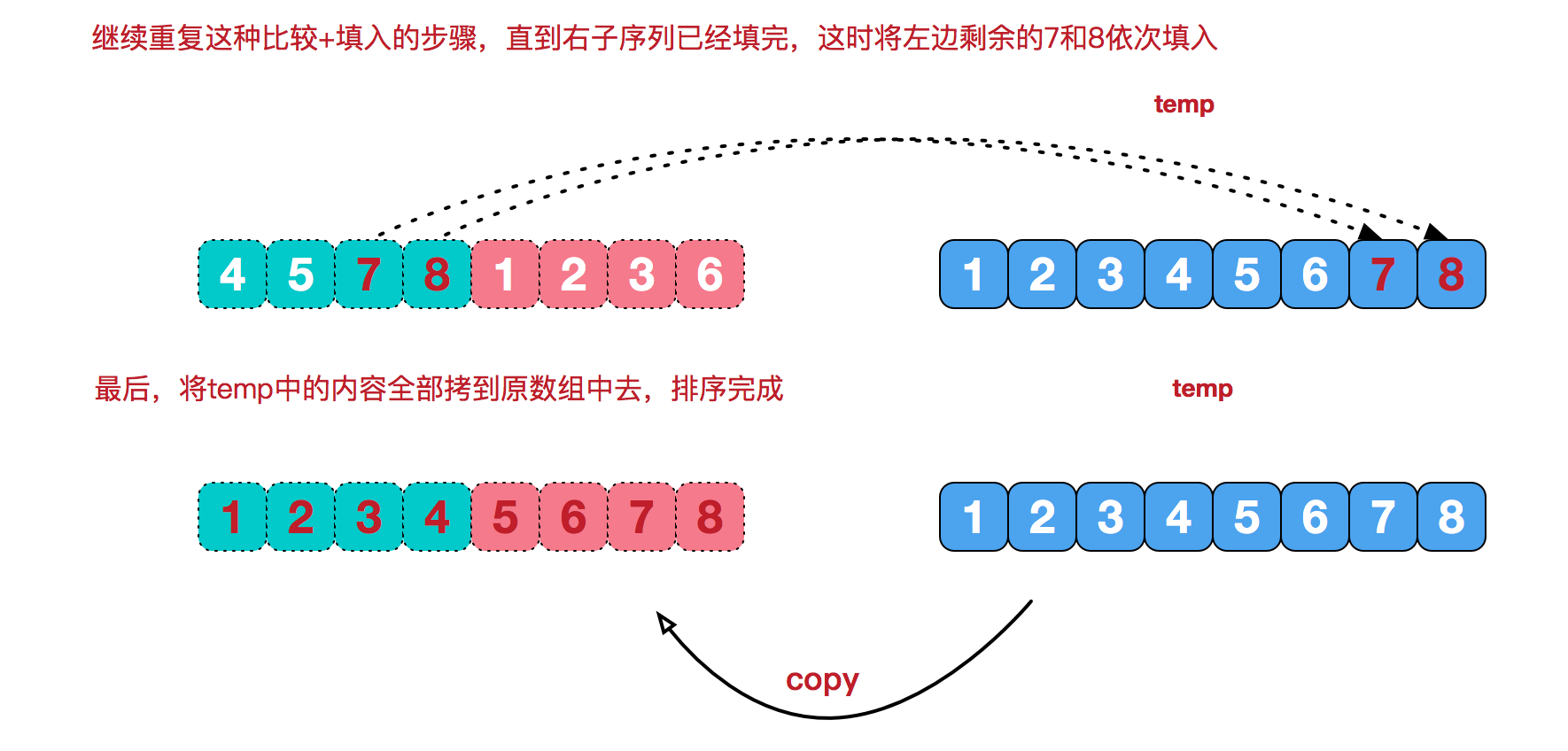
　　再来看看治阶段，我们需要将两个已经有序的子序列合并成一个有序序列，比如上图中的最后一次合并，要将[4,5,7,8]和[1,2,3,6]两个已经有序的子序列，合并为最终序列[1,2,3,4,5,6,7,8]，来看下实现步骤。