这个算法经常用,例如GIS,数据保存,数据绘制都会用到。
算法是1973提出的,久经考验的算法,具体详情可以参考百度。
算法比较简单,大意是:
① 给出一个限定值表示距离
② 点集合或者坐标集合的首尾自动相连接成为直线,并会记录首尾两点到输出集合
③ 记录后寻找集合中距离这个直线最远的点,当这个点的距离超过限定值时,记录这个点,并由此将集合分为两段,首到点,点到尾
④ 对每个线段重复步骤②,步骤③,直至结束
也可以参考其他网友给出的算法推导.
其中 找出最远点的点的算法,可以利用 三个点形成的面积,也就是三角形的面积。
其中求出点到线的距离,也就是三角形的高。
我们可以认为首尾连接的线是底部边,我们有底部边的起点和终点坐标,可以利用向量公式,尾坐标减去首坐标,求出向量坐标后,再利用向量的求模公式求出长度。
最后三角形面积除以底的长度乘与2就等于高度了。
截图
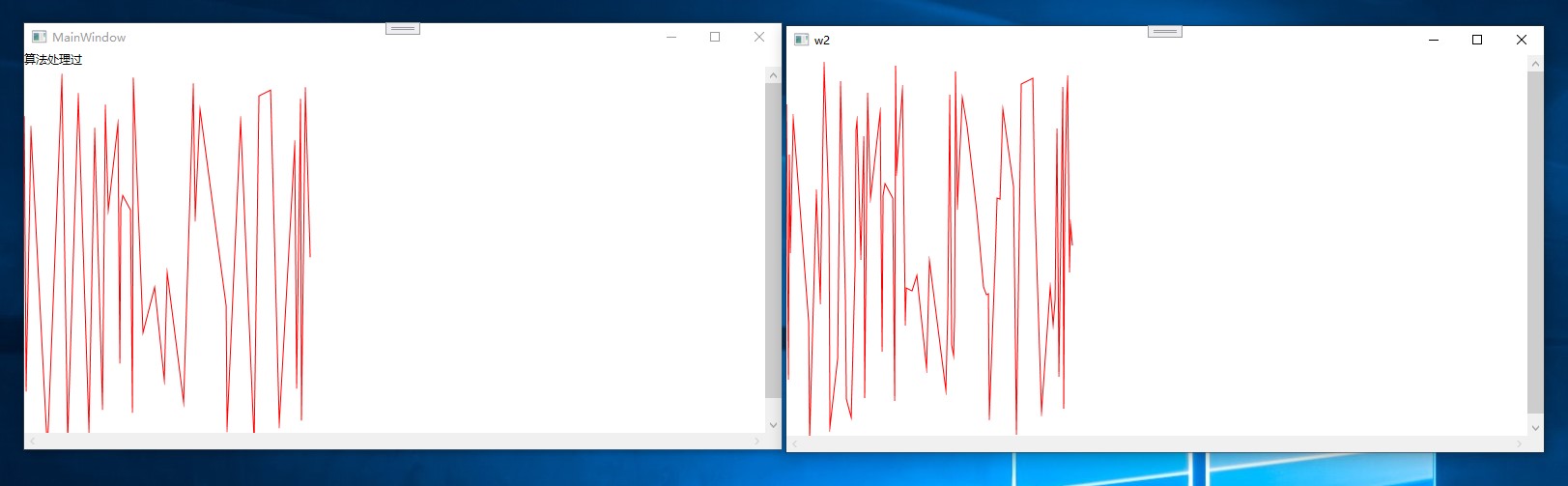
代码是现成的,虽然实现也不困难, 偷懒....
public class Douglas_Peucker { /// <summary> /// Douglas-Peucker算法 /// </summary> /// <param name="Points">坐标点集合</param> /// <param name="Tolerance">限定值</param> /// <returns></returns> public static List<Point> DouglasPeuckerReduction (List<Point> Points, Double Tolerance) { if (Points == null || Points.Count < 3) return Points; Int32 firstPoint = 0; Int32 lastPoint = Points.Count - 1; List<Int32> pointIndexsToKeep = new List<Int32>(); //默认添加首尾两点 pointIndexsToKeep.Add(firstPoint); pointIndexsToKeep.Add(lastPoint); //首尾两点不能相同 while (Points[firstPoint].Equals(Points[lastPoint])) { lastPoint--; } //递归计算 DouglasPeuckerReduction(Points, firstPoint, lastPoint, Tolerance, ref pointIndexsToKeep); //返回集合 List<Point> returnPoints = new List<Point>(); pointIndexsToKeep.Sort(); foreach (Int32 index in pointIndexsToKeep) { returnPoints.Add(Points[index]); } return returnPoints; } /// <summary> /// 递归计算每个点到线段的长度,并分段递归重复计算 /// </summary> /// <param name="points">点集合</param> /// <param name="firstPoint">首点</param> /// <param name="lastPoint">尾点</param> /// <param name="tolerance">限定值</param> /// <param name="pointIndexsToKeep">点集合下标</param> private static void DouglasPeuckerReduction(List<Point> points, Int32 firstPoint, Int32 lastPoint, Double tolerance, ref List<Int32> pointIndexsToKeep) { Double maxDistance = 0; Int32 indexFarthest = 0; //遍历每个点 for (Int32 index = firstPoint; index < lastPoint; index++) { Double distance = PerpendicularDistance (points[firstPoint], points[lastPoint], points[index]); //只寻找线段上最长的点 if (distance > maxDistance) { //替换值 maxDistance = distance; //记录下标 indexFarthest = index; } } //确定最大值超过限定值且不为首点 if (maxDistance > tolerance && indexFarthest != 0) { //记录最大距离的点的下标 pointIndexsToKeep.Add(indexFarthest); //分段计算 Startpoint-MaxDistance DouglasPeuckerReduction(points, firstPoint, indexFarthest, tolerance, ref pointIndexsToKeep); //分段计算 MaxDistance-Lastpoint DouglasPeuckerReduction(points, indexFarthest, lastPoint, tolerance, ref pointIndexsToKeep); } } /// <summary> /// 求出点到两点的距离 /// </summary> /// <param name="pt1">线段的起点</param> /// <param name="pt2">线段的终点</param> /// <param name="p">计算的点</param> /// <returns></returns> public static Double PerpendicularDistance (Point Point1, Point Point2, Point Point) { //Area = |(1/2)(x1y2 + x2y3 + x3y1 - x2y1 - x3y2 - x1y3)| *Area of triangle //Base = v((x1-x2)²+(x1-x2)²) *Base of Triangle* //Area = .5*Base*H *Solve for height //Height = Area/.5/Base //求面积 Double area = Math.Abs(.5 * (Point1.X * Point2.Y + Point2.X * Point.Y + Point.X * Point1.Y - Point2.X * Point1.Y - Point.X * Point2.Y - Point1.X * Point.Y)); //求首尾两点的长度 Double bottom = Math.Sqrt(Math.Pow(Point1.X - Point2.X, 2) + Math.Pow(Point1.Y - Point2.Y, 2)); //三角形面积除以底*2=高 //三角形面积除以高*2=底 Double height = area / bottom * 2; return height; //Another option //Double A = Point.X - Point1.X; //Double B = Point.Y - Point1.Y; //Double C = Point2.X - Point1.X; //Double D = Point2.Y - Point1.Y; //Double dot = A * C + B * D; //Double len_sq = C * C + D * D; //Double param = dot / len_sq; //Double xx, yy; //if (param < 0) //{ // xx = Point1.X; // yy = Point1.Y; //} //else if (param > 1) //{ // xx = Point2.X; // yy = Point2.Y; //} //else //{ // xx = Point1.X + param * C; // yy = Point1.Y + param * D; //} //Double d = DistanceBetweenOn2DPlane(Point, new Point(xx, yy)); } }
使用这个算法后,能够将点减少很多,在视觉上差距不大,适用于很多点的时候,绘制困难,通过这个算法减少点的数量.