数据标准化与Python实现

一、原理
        数据标准化（Normalization）：将数据按照一定比例进行缩放，使其落入到一个特定的小区间。

数据标准化的类别：

• Min-Max标准化
• Z-Score标准化（Standard Score，标准分数）
• 小数定标（Decimal scaling）标准化
• 均值归一化
• 向量归一化
• 指数转换

1、Min-Max标准化
        Min-Max标准化，指对原始数据进行线性变换，将值映射到[0,1]之间。

公式：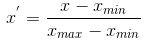

式中，x为原始数据的数据，x_min为原始数据的最小值，x_max为原始数据的最大值。

2、Z-Score标准化

        又称为Standard Score（标准分数），指基于原始数据的均值（mean）和标准差（standard deviation）来进行数据的标准化。

公式：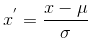

式中，x为原始数据的数据，μ为原始数据的均值，σ为原始数据的标准差。

3、小数定标（Deciaml scaling）标准化
        指通过移动小数点的位置来进行数据的标准化。小数点移动的位数取决于原始数据中的最大绝对值。

公式：

式中，x为原始数据，10^j的j表示最大绝对值的位数。

例如，现在有一个数组[-309, -10, -43, 87, 344, 970]，其中最大绝对值为970，即j=3，标准化为的数据为[-0.309, -0.01, -0.043, 0.087, 0.344, 0.97]

4、均值归一化
        指通过原始数据中的均值、最大值和最小值来进行数据的标准化。

公式：

式中，x为原始数据，μ为原始数据的均值，x_min为原始数据的最小值，x_max为原始数据的最大值。当然，分母部分也可以使用x_max代替。

5、向量归一化
        指通过原始数据中的每个值除以所有数据之和来进行数据的标准化。

公式：

式中，x为原始数据，分母为所有数据之和。

6、指数转换
        指通过对原始数据的值进行相应的指数函数变换来进行数据的标准化。进行指数转换常见的函数方法有lg函数、Softmax函数和Sigmod函数。

公式：

（1）lg函数：

 

式中，x为原始数据，为原始数据的最大值。

（2）Softmax函数：

 

式中，x为原始数据，e为自然对数，分母表示的是原始数据中每个数据对e求指数后的和。

（3）Sigmoid函数：

二、代码实现数据的标准化

import numpy as np
import math
 
class DataNum:
    def __init__(self):
        self.arr = [1.0,2.0,3.0,4.0,5.0,6.0,7.0,8.0,9.0]
        self.x_max = max(self.arr)  # 最大值
        self.x_min = min(self.arr)  # 最小值
        self.x_mean = sum(self.arr) / len(self.arr) # 平均值
        self.x_std = np.std(self.arr)   # 标准差
        print("原始数据：
{}".format(self.arr))
 
    def Min_Max(self):
        arr_ = list()
        distance = self.x_max-self.x_min
        for x in self.arr:
            arr_.append(round((x-self.x_min)/distance,4))   # 保留4位小数
        print("Min_Max标准化结果：
{}".format(arr_))
 
    def Z_Score(self):
        arr_ = list()
        for x in self.arr:
            arr_.append(round((x-self.x_mean)/self.x_std,4))
        print("Z_Score标准化结果：
{}".format(arr_))
 
    def DecimalScaling(self):
        arr_ = list()
        j = self.x_max // 10 if self.x_max % 10 == 0 else self.x_max // 10 + 1
        for x in self.arr:
            arr_.append(round(x/(math.pow(10,j)),4))   # 保留4位小数
        print("DecimalScaling标准化结果：
{}".format(arr_))
 
    def Mean(self):
        arr_ = list()
        distance = self.x_max - self.x_min
        for x in self.arr:
            arr_.append(round((x - self.x_mean) / distance, 4))  # 保留4位小数
        print("Mean标准化结果：
{}".format(arr_))
 
    def Vector(self):
        arr_ = list()
        arr_sum = sum(self.arr)
        for x in self.arr:
            arr_.append(round(x / arr_sum, 4))  # 保留4位小数
        print("Vector标准化结果：
{}".format(arr_))
 
    def exponential(self):
        arr_1 = list()  # lg
        arr_2 = list()  # SoftMax
        arr_3 = list()  # Sigmoid
        sum_e = sum([math.exp(x) for x in self.arr])
        for x in self.arr:
            arr_1.append(round(math.log10(x) / math.log10(self.x_max), 4))  # 保留4位小数
            arr_2.append(round(math.exp(x) / sum_e, 4))  # 保留4位小数
            arr_3.append(round(1 / (1+math.exp(-x)), 4))  # 保留4位小数
        print("lg标准化结果：
{}".format(arr_1))
        print("SoftMax标准化结果：
{}".format(arr_2))
        print("Sigmod标准化结果：
{}".format(arr_3))
 
    def do(self):
        dn.Min_Max()
        dn.Z_Score()
        dn.DecimalScaling()
        dn.Mean()
        dn.Vector()
        dn.exponential()
 
if __name__ == '__main__':
    dn = DataNum()
    dn.do()

运行结果：