1 效用理论概述
1.1 效用的概念
1.1.1 效用
效用(utility):消费者在消费商品或服务时所感受到的满足。
三个特点:
1、效用是消费者对商品和服务的主观评价。
2、效用因人、因时、因地而不同。
3、效用本身不包括有关是非的价值判断。
1.2 效用理论的基本假设
1.2.1 完全信息
效用理论假设:消费者已经掌握与消费决策有关的全部信息,他们知道所有可获得的商品和服务的范围,以及它们能提供的效用。各种商品的价格同样为消费者所知,消费者在这段时间内的收入也是已知的。
1.2.2 偏好次序
偏好次序:消费者有能力将所有商品分组排序。消费者在面对两个或两个以上的商品组时,能够决定对它们的偏好排序。
如:麦当劳和肯德基:一样喜欢;偏好其中一种;
1.3 基数效用与序数效用
1.3.1 基数效用论
基数效用论:形成于19世纪。效用是一个数量概念。认为,一种商品或劳务效用的大小,可以用基数(1,2,3· · ·)测量。衡量单位是效用单位(Util,尤特尔)。
例如:吃一个面包得到的满足是4 Utils
看一场电影的满足是8 Utils
1.3.2 序数效用论
序数效用论:产生于20世纪30年代。效用是一个次序概念。认为,效用的绝对量大小根本无法测定,无法用某种统一的单位表示出来,它们只能根据消费者的个人偏好程度排列出效用大小先后的顺序。
例如:阿珂在苹果和桃子中,选择了苹果,放弃了桃子。则对我而言,苹果的效用大于桃子。或者说苹果效用第一(最大),桃子效用第二(次之)。
2 基数效用论与边际效用分析
2.1 总效用与边际效用
总效用(total Utility, TU)与边际效用(marginal Utility, MU)
总效用(TU):指消费者在一定时期内从一定数量的商品消费中获得的效用量的总和。
边际效用(MU) :指消费者在一定时间内增加一单位商品的消费时,所获得的总效用量的增量。
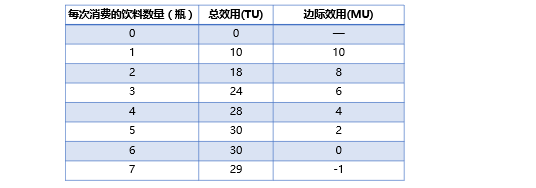
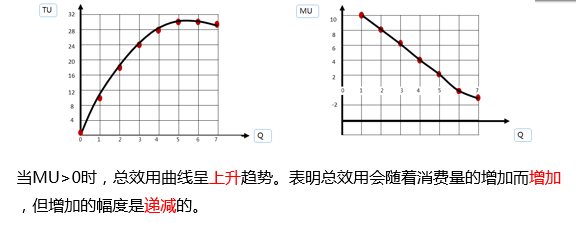

总效用与边际效用的关系:
MU>0时,总效用曲线呈上升趋势。
MU=0时,总效用曲线达到最高点,总效用取得最大值。(即:总效用最大时,边际效用等于0)
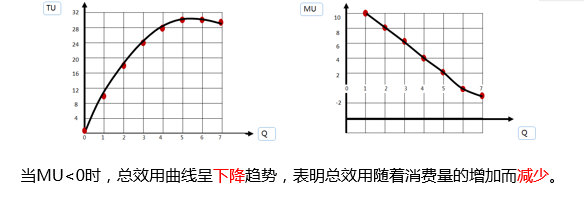
MU<0时,总效用曲线呈下降趋势。
2.2 边际效用递减规律
边际效用递减规律:随着消费数量增加,边际效用呈下降趋势的现象。
某一种商品的边际效用大小,主要取决于商品消费量的大小。

2.3 求导
当题目给出函数,让我们求边际的时候,要用到导数。
求导:通过原函数,得到导数。这个过程就叫做求导。

偏导数:原函数里面有两个自变量
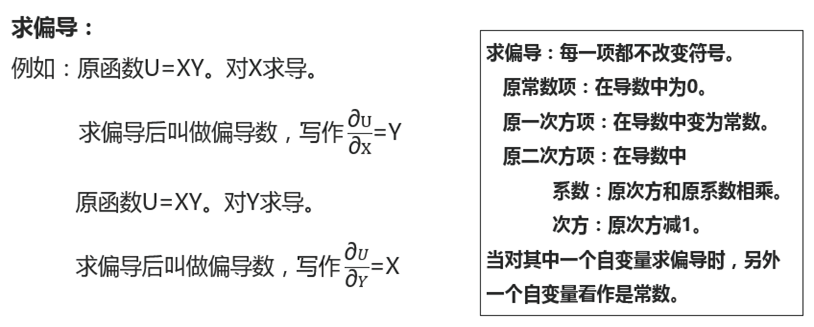
z = x2+2x+y2+3y
x 的偏导(将y看做是一个常数,y2和3y都是常数项)
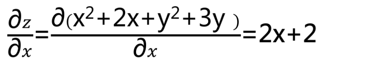
y的偏导(将x看做是一个常数,x2和2x都是常数项)

2.4 消费者均衡
消费者均衡:单个消费者把有限的货币收入分配在对各种商品的购买中获得效用的最大化。
假设消费者用收入I,只消费两种商品X和Y,其效用函数:U=U(X,Y)。
X商品的价格为PX,Y商品的价格为PY,于是收入约束为:PXX+ PyY=I。
 该消费者效用最大化的条件为:
该消费者效用最大化的条件为:
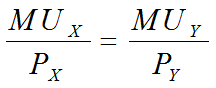
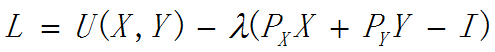
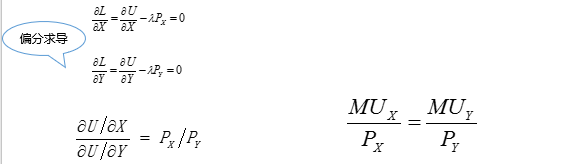
均衡条件的含义:消费者使自己花费在各种商品购买上的最后一元钱带来的边际效用相等,也称等边际效用原则。
也就是,我的最后一块钱用来购买商品X或者Y得到的效用是一样的。
2.4.1 例题1
已知某消费者每月用2400元购买X和Y商品,他的效用函数为U=XY,X商品的价格为20元,Y商品的价格为30元,为获得最大效用,该消费者应该购买X商品和Y商品各为多少?


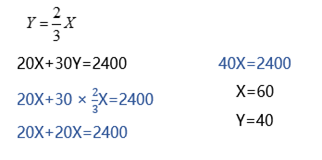
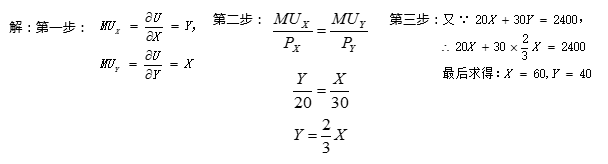
步骤总结:
1、利用总效用函数,求商品X和Y的边际效用。(一般都是求偏导)
2、利用消费者均衡条件
3、利用总价钱的约束条件分别确定商品的价格。
2.4.2 例题2
如果消费者消费的X、Y商品的价格之比是1.25,它们的边际效用之比是2,为达到效用最大化,消费者应(增购X和减少购买Y)
解:由题可知:
MUx/MUy =2 ====> MUx=2MUy
Px/Py = 1.25 ====> Px = 1.25Py
MUx/Px = 2MUy/1.25Py=1.6 MUy/ Py
所以可得: MUx/Px > MUy/ Py

2.4.3 例题3
某人每周花费360元买X和Y两种商品,且Px = 3 , Py = 2 ,效用函数为U=2X2Y,求在均衡 状态下他如何购买效用最大.

说明:对X求导时,将Y看做常数,X未知,所以MUX = 4xy
对y 求导时,将X看做常数,Y未知,所以MUy = 2X2

2.5 消费者剩余
消费者剩余:消费者愿意为某一商品支付的价格与在购买该商品时实际支付的价格之间的差额。
一:并不是实际收入增加,只是一种心理感觉。
二:生活必需品的消费者剩余大。
3 序数效用论与无差异曲线分析
3.1 序数效用论
序数效用论:效用是一个次序概念。认为,效用的绝对量大小根本无法测定,无法用某种统一的单位表示出来,它们只能根据消费者的个人偏好程度排列出效用大小先后的顺序。
消费者偏好:消费者对任意两个商品组合所做的一个排序。
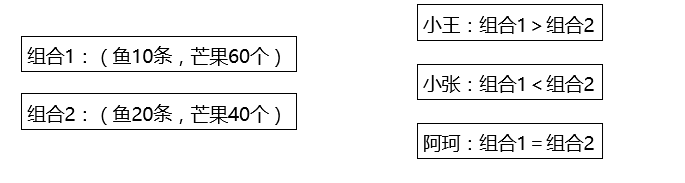
序数效用论用无差异曲线分析法来说明消费者均衡的实现。
3.2 无差异曲线
3.2.1 无差异曲线的性质
无差异曲线:表示消费者偏好相同的两种商品的不同数量的各种组合。
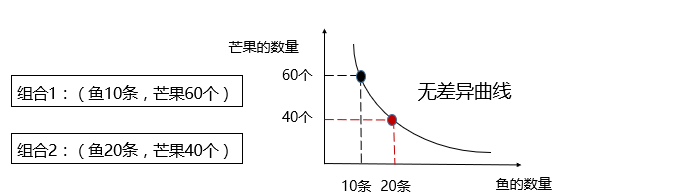
无差异曲线的性质:
(1)无差异曲线是向右下方倾斜,凸向原点。
(2)同一条无差异曲线表示两种商品的不同数量的组合给消费者提供的效用是相同的。
(3)任意两条无差异曲线之间不能相交。
(4)离原点越远的无差异曲线所代表的效用水平越高。

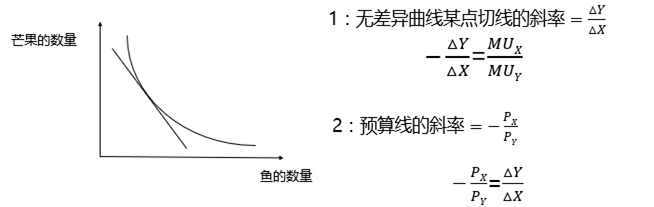
3.2.2 边际替代率
1、边际替代率(Marginal Rate of Substitution,MRS) :消费者在保持自己效用水平不变的情况下,为了增加一种商品X的消费量所愿意放弃的另一种商品Y的消费量。



3.3 消费者的预算线
3.3.1 预算线
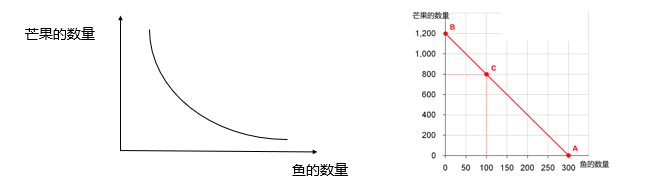
预算线(budget line):在给定的价格和收入下,消费者把所有收入用于消费所能获得的商品组合点的轨迹。

总收入为I。
鱼的价格为PX,鱼买X条。
芒果的价格为PY,芒果买Y个。
则预算线怎么表示?
PYY+PXX=I

若:消费者所有的收入(I)都用于购买商品X和Y,商品X和Y的价格分别为PX和PY,则预算线可用方程表示为:
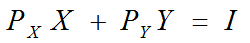
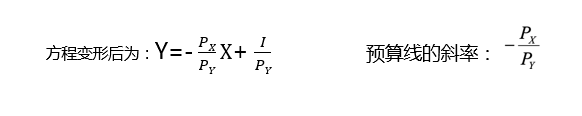
3.3.1.1 例题1
小明现在预备用1000元来购买牛肉和大米,牛肉的价格为每斤20元,大米的价格为每斤5元。
(1)请写出小明购买牛肉和大米的预算线方程。
(2)如果以牛肉的购买量为纵轴,大米的购买量为横轴,预算线的斜率为多少?
(3)如果大米的价格降低到每斤4元,请写出新的预算线方程。
解:
(1)假设大米的购买量为X,牛肉的购买量为Y,则预算线方程为:1000=5X+20Y
(2)如果以牛肉的购买量为纵轴,大米的购买量为横轴,以上预算线可以改写为: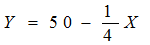
预算线的斜率为:-
(3)如果大米的价格降低到每斤4元,新的预算线方程为:1000=4X+20Y
3.3.1.2 例题2
某人用400元的收入购买X、Y两种商品,PX=100元,PY=50元。
1. 写出该消费者的预算线方程;
2. 假设X价格降为50元,其它不变,写出消费者的预算线方程;
3. 假设收入降为300元,PX=PY=50元。写出消费者的预算线方程。
解: 1、该消费者的预算线方程是400 =100X + 50Y
2、400=50X+50Y
3、300 = 50X+50Y
3.3.2 消费者预算线的变化
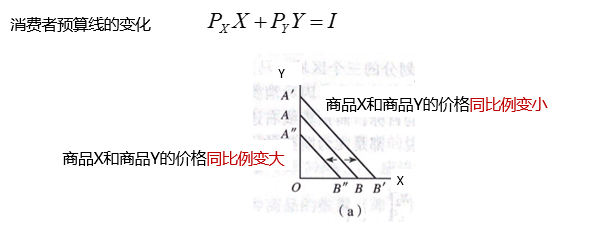
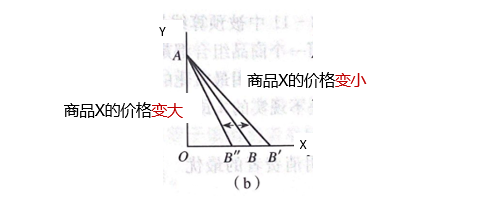
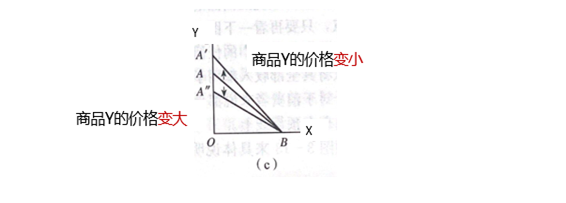
3.4 消费者均衡
消费者均衡:在预算给定的情况下,消费者通过决定两种商品的消费量使得自己的效用最大化的状态。


已知商品X和Y的价格既定,当MRS>Px/Py时,消费者如要得到最大效用,他应该(增加购买X和减少购买Y)
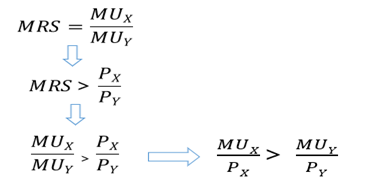

解:
1、PY=10,QY=50
则消费者收入为:10×50=500
2、QX=40
则PX=500÷40=12.5
3、预算线方程:
10Y+12.5X=500
4、E点的边际替代率为斜率:
则为1.25