我们通常所说的排序算法往往指的是内部排序算法,即数据记录在内存中进行排序。
排序算法大体可分为两种:
一种是比较排序,时间复杂度O(nlogn) ~ O(n^2),主要有:冒泡排序,选择排序,插入排序,归并排序,堆排序,快速排序等。
另一种是非比较排序,时间复杂度可以达到O(n),主要有:计数排序,基数排序,桶排序等。
下表给出了常见比较排序算法的性能:

为了便于以下描述,接下来全部算法的排序对象均为乱序数组int a[n];
-
冒泡排序(BubbleSort)
思路:对相邻的两个元素进行比较,这样每轮比较完当前最大(小)的元素就会移到尾部,如此重复n轮,便可实现排序。
实现:
1 void bubbleSort(int a[],int begin,int end) 2 { 3 for(int i = begin;i<end;i++) 4 { 5 for(int j = i+1;j<end;j++) 6 { 7 if(a[i]>a[j]) 8 { 9 std::swap(a[i],a[j]); 10 } 11 } 12 } 13 }
具体排序过程如图:
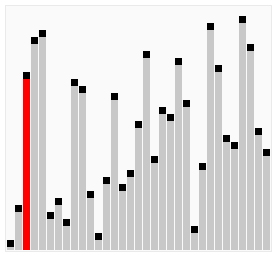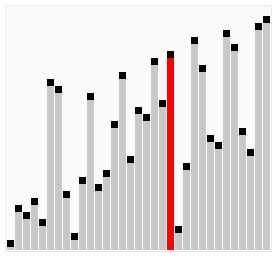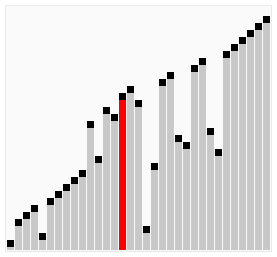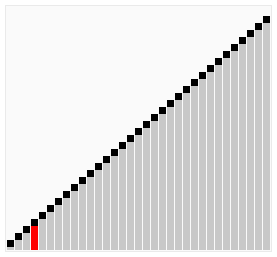
总结:
最简单排序算法,稳定,由于两层循环因此复杂度为O(n2)。(但是想到当年第一次找工作时被问到,结果不出所料没有答出来,真是让我觉得难堪的算法。)
-
归并排序
归并排序是经典排序算法中三个复杂度为O(nlgn)中唯一的稳定算法,其主要思想就是将当前数组划分成两个有序部分,再利用O(n)的时间把两个有序部分进行合并。其中划分最小数组存在迭代与递归两种版本。
两种版本通用部分Merge算法:
1 void merge(int a[], int begin, int mid, int end) 2 { 3 int count = end - begin + 1; 4 int* p = new int[count](); 5 int i = begin, j = mid + 1, index = 0; 6 while (i <= mid && j <= end) 7 { 8 p[index++] = a[i] <= a[j] ? a[i++] : a[j++]; 9 } 10 while (j <= end) 11 p[index++] = a[j++]; 12 while (i <= mid) 13 p[index++] = a[i++]; 14 for (int i = 0; i < count; i++) 15 { 16 a[begin++] = p[i]; 17 } 18 delete[]p; 19 }
实现(递归):
1 void mergeSort_Recursion(int a[], int begin, int end) 2 { 3 if (begin >= end) return; 4 int mid = (begin + end) / 2; 5 mergeSort_Recursion(a, begin, mid); 6 mergeSort_Recursion(a, mid + 1, end); 7 merge(a, begin, mid, end); 8 }
思路:
- 递归对该数组每次进行二分,如此不断重复下去直到当前数组被划分成n个大小为1数组,然后两两合并,当合成更大的有序数组时,再次进行两两合并,以此类推直至整个数组有序。
- 归并排序的端点情况有点麻烦,至少我在实现的时候被坑了很多次,最后参考别人代码实现(尴尬)。
实现(迭代):
1 void mergeSort_Iteration(int a[], int begin, int end) 2 { 3 int count = end - begin + 1; 4 int left; 5 for (int step = 1; step < count; step *= 2) 6 { 7 //immitate recursion mannully 8 left = begin; 9 while (left + step < end) 10 { 11 int mid = left + step - 1; 12 int right = (mid + step ) < end ? (mid + step) : end; 13 merge(a, left, mid, right); 14 left = right + 1; 15 } 16 } 17 }
思路:迭代与递归的唯一区别在于如何获取到最小的数组,迭代在于从大小为1的数组开始,每次处理的数组大小长度扩大2倍,直到处理长度大于整个数组的长度为止;而递归则是每次二分直到最后划分成大小为1的数组,二者可以理解为相反的过程。
其实现可以看图:

-
堆排序
来源百度百科:
堆排序(Heapsort)是指利用堆积树(堆)这种数据结构所设计的一种排序算法,它是选择排序的一种。可以利用数组的特点快速定位指定索引的元素。堆分为大根堆和小根堆,是完全二叉树。
前面我已经有二叉树入门的文章了,当时讲解的是二叉查找树,那上面所说的完全二叉树是怎么样的一种二叉树呢??还有满二叉树又是怎么的一种二叉树呢??甚至还有完满二叉树??
- 完全二叉树: 除了最后一层之外的其他每一层都被完全填充,并且所有结点都保持向左对齐。
- 满二叉树:除了叶子结点之外的每一个结点都有两个孩子,每一层(当然包含最后一层)都被完全填充。
- 完满二叉树:除了叶子结点之外的每一个结点都有两个孩子结点。
下面用图来说话:
- 完全二叉树(Complete Binary Tree):
- 满二叉树(Perfect Binary Tree):
- 完满二叉树(Full Binary Tree):
参考资料:https://www.cnblogs.com/Java3y/p/8639937.html
简单来说:堆排序是将数据看成是完全二叉树、根据完全二叉树的特性来进行排序的一种算法
- 最大堆要求节点的元素都要不小于其孩子,最小堆要求节点元素都不大于其左右孩子
- 那么处于最大堆的根节点的元素一定是这个堆中的最大值
实现:
1 void heapify(int a[],int cur,int size) 2 { 3 int lChild = 2*cur+1; 4 int rChild =2*cur+2; 5 int max = cur; 6 if(lChild < size && a[max] < a[lChild]) 7 max = lChild; 8 if(rChild < size && a[max] < a[rChild]) 9 max = rChild; 10 if(cur != max) 11 { 12 std::swap(a[cur],a[max]); 13 //当前节点移动到其左右孩子节点,继续递归调用,直到该节点比其孩子都大 14 heapify(a,max,size); 15 } 16 }
思考:堆排序最重要的就是构成最大(小)堆,而对于每一个非叶子节点元素,需要保证其的值始终比其左右节点(如果有的话)大(小),那么Heapify()函数则实现了把某一个元素在建堆时的正确归位。
建堆:
1 void buildHeap(int a[],int n) 2 { 3 //对于n个元素,最后一个元素的父节点可以表示为n/2-1; 4 for(int i = n/2-1;i>=0;i--) 5 //除去全部叶子节点,生产最大堆 6 heapify(a,i,n); 7 }
思考:除去叶子节点,其余全部节点从最后一个节点的父节点开始逆序执行上面的heapify函数进行建堆。这里由于一共n个元素,因此最后一个元素为n-1,那么其父节点可以表示成(n-1)/2(具体可以画图很容易得到关系)。
堆排:
1 void heapSort(int a[],int left,int right) 2 { 3 int size = right - left+1; 4 buildHeap(a,size); 5 //当未排序的数目大于1时 6 while(size>1) 7 { 8 //堆顶为当前堆中最大元素,置换到数组尾部 9 std::swap(a[0],a[--size]); 10 //堆顶元素不满足条件,重新建堆 11 heapify(a,0,size); 12 } 13 }
思考:当建堆完毕后,第一个元素即堆顶元素将会是最大(小)的元素,那么与最后一个元素交换即可得到一个已排序好的数组,但这会导致整个堆乱序,于是再对堆顶元素调用一次heapify函数,如此反复,直到整个堆中元素只剩下一个为止。
实现过程:
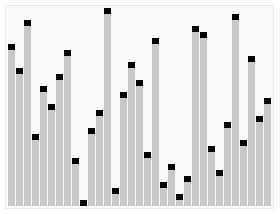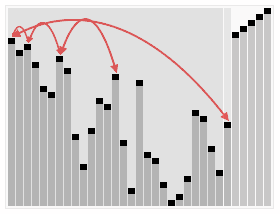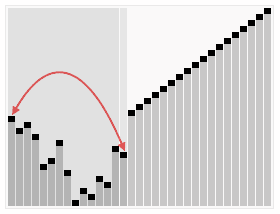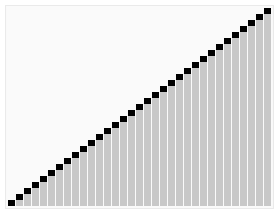
堆排序是不稳定的排序算法,不稳定发生在堆顶元素与A[i]交换的时刻。
-
快速排序
快速排序可以理解为冒泡的进阶,在最优条件下,即每次都找到的基准都可以均分数组,此时可以得到O(nlgn)的复杂度,而最差情况则退化成冒泡排序O(n2)。
思路:对于一个数组,寻找一个基准,然后凡是比基准小均放到左侧,最后便可以按照记住把当前数组分成两部分。然后对两部分再寻找新基准重复上面的方法,直到每个部分被划分为大小为1的部分,至此完成排序。
或者可以参考百度百科解释:
通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另外一部分的所有数据都要小,然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序。
寻找基准分区:
1 int partition(int a[],int left, int right) 2 { 3 //基准 4 int pivot = a[right]; 5 int tail = left-1; 6 for(int i = left;i<right;i++) 7 { 8 if(a[i]<=pivot) 9 { 10 std::swap(a[i],a[++tail]); 11 } 12 } 13 std::swap(a[tail+1],a[right]); 14 return tail+1; 15 }
递归实现:
1 void quickSort(int a[],int left, int right) 2 { 3 if(left<right) 4 { 5 int pivot = partition(a,left,right); 6 quickSort(a,left,pivot-1); 7 quickSort(a,pivot+1,right); 8 } 9 }
思考:先计算出基准,然后按照基准划分的两部分,递归调用快排算法即可。
优化:
1 void quickSort(int a[],int left, int right) 2 { 3 while(left < right) 4 { 5 int pivot = partition(a,left,right); 6 quickSort(a,left,pivot-1); 7 left = pivot+1; 8 } 9 }
思考:与普通递归相比,由于尾递归的调用处于方法的最后,因此方法之前所积累下的各种状态对于递归调用结果已经没有任何意义,因此完全可以把本次方法中留在堆栈中的数据完全清除,把空间让给最后的递归调用。这样的优化1便使得递归不会在调用堆栈上产生堆积,意味着即时是“无限”递归也不会让堆栈溢出。