给定一个 N 叉树,找到其最大深度。
最大深度是指从根节点到最远叶子节点的最长路径上的节点总数。
例如,给定一个 3叉树 :
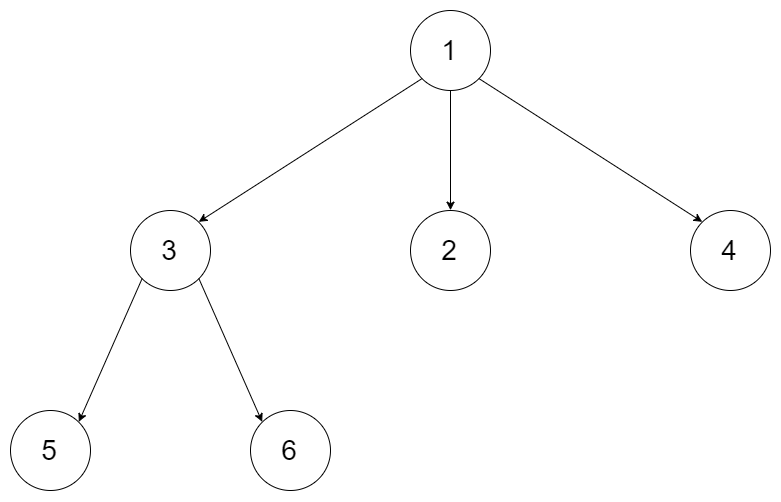
我们应返回其最大深度,3。
说明:
树的深度不会超过 1000。
树的节点总不会超过 5000。
soultion1:
1 /* 2 // Definition for a Node. 3 class Node { 4 public: 5 int val; 6 vector<Node*> children; 7 8 Node() {} 9 10 Node(int _val, vector<Node*> _children) { 11 val = _val; 12 children = _children; 13 } 14 }; 15 */ 16 class Solution { 17 public: 18 int maxDepth(Node* root) { 19 int depth = 0; 20 if(root!=nullptr) 21 { 22 queue<Node*>q; 23 q.push(root); 24 while(!q.empty()) 25 { 26 depth++; 27 //cur level's node count 28 int size = q.size(); 29 while(size-->0) 30 { 31 //count cur level's node 32 auto first = q.front(); 33 q.pop(); 34 for(auto node : first->children) 35 { 36 //for next level 37 q.push(node); 38 } 39 } 40 } 41 } 42 return depth; 43 } 44 };
思考:层次遍历解法,稍微变化的点时记录当前层节点数目k,然后让队列弹出k个元素,此时队列内的元素即全为下一层的子元素,此时深度+1即可。
solution2:
1 /* 2 // Definition for a Node. 3 class Node { 4 public: 5 int val; 6 vector<Node*> children; 7 8 Node() {} 9 10 Node(int _val, vector<Node*> _children) { 11 val = _val; 12 children = _children; 13 } 14 }; 15 */ 16 class Solution { 17 public: 18 int maxDepth(Node* root) { 19 if(root == nullptr) return 0; 20 int maxD= 0; 21 for(auto child : root->children) 22 { 23 maxD = max(maxD,maxDepth(child)); 24 } 25 return maxD+1; 26 } 27 };
思考:对于递归的操作:
- 1.递归终止条件
- 2.每层递归需要做的事情:分别求出当前节点子节点的最大深度,然后求出其最大值,最大值+1即为最大深度
感觉已经完全看不懂递归了