The Unique MST POJ

题意：求一个无向图的最小生成树，如果有多个最优解，输出"Not Unique!"

题解：

　　考虑kruskal碰到权值相同的边：

　　假设点3通过边（1，3）连入当前所维护的并查集s。

　　然后有一条边（下图蓝色的边）满足：

　　　　　　1.长度等于（1，3） 

　　　　　　2.一端连到3，一端连入S。

　　那么该边可以替换掉（1，3）。产生另一颗最小生成树。

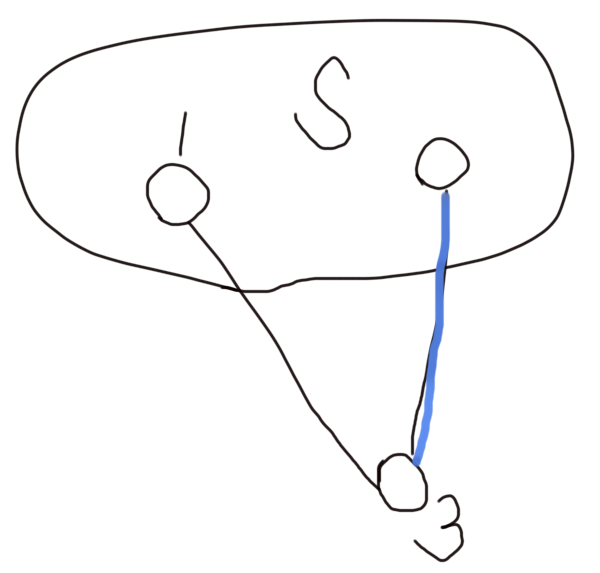
 关于如何判断该边一端连3，一端连入S，

用set来记录S中的点，find判断点是否在集合内。（发现kruskal可以用set写啊）

#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#include<queue>
#include<algorithm>
#include<iostream>
#include<vector>
#include<string.h>
#include<set>
using namespace std;
const int maxn = 3e4;;set<int> s;
struct edge {
    int to, from, w;
    edge(int to=0, int from=0, int w=0) :to(to), from(from), w(w) {}
}e[maxn];
bool cmp(edge a, edge b) {
    return a.w < b.w;
}
int f[maxn];
int find(int x) {
    return f[x] == x ? x : f[x] = find(f[x]);
}
void un(int x, int y) {
    int u = find(x), v= find(y);
    f[u] = v;
}
bool same(int x, int y) {
    return find(x) == find(y);
}
int main() {
    int t;
    cin >> t;
    while (t--)
    {
        int n, m; cin >> n >> m;
        int num = 0;
        for (int i = 0; i < m; i++) {
            int x, y, z; cin >> x >> y >> z;
            e[num++] = edge(x, y, z);
        }
        for (int i = 1; i <= n; i++)f[i] = i;
        sort(e, e + m,cmp);
        int lastw = -1, lastto = -1, lastfrom = -1,lastv = -1;
        int res=0, flag=0;
        for (int i = 0; i < m; i++) {

            if (same(e[i].to, e[i].from)) {
                if (e[i].w == lastw) {            
                    if (e[i].to == lastv && (s.find(e[i].from) != s.end())) { flag = 1; break; }
                    if (e[i].from == lastv && (s.find(e[i].to) != s.end())) { flag = 1; break; }
                }
                continue;
            }
            un(e[i].to, e[i].from);
　　　　　　　　res += e[i].w;
            if (s.find(e[i].to) == s.end()) lastv = e[i].to;
            else lastv = e[i].from;
            s.insert(e[i].to);
            s.insert(e[i].from);
        }
        if (flag)cout << "Not Unique!";
        else cout << res;
        cout << endl;
    }
}

队友的玄学代码（改）可以不断记录上一条被选择的边，每次选边时判断一下入度出度关系；

#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#include<queue>
#include<algorithm>
#include<iostream>
#include<vector>
#include<string.h>
using namespace std;
const int maxn = 3e4;;
char s[maxn], str[maxn];
int len1, len2, p[maxn], ans;
struct edge {
    int to, from, w;
    edge(int to=0, int from=0, int w=0) :to(to), from(from), w(w) {}
}e[maxn];
bool cmp(edge a, edge b) {
    return a.w < b.w;
}
int f[maxn];
int find(int x) {
    return f[x] == x ? x : f[x] = find(f[x]);
}
void un(int x, int y) {
    int u = find(x), v= find(y);
    f[u] = v;
}
bool same(int x, int y) {
    return find(x) == find(y);
}
int main() {
    int t;
    cin >> t;
    while (t--)
    {
        int n, m; cin >> n >> m;
        int num = 0;
        for (int i = 0; i < m; i++) {
            int x, y, z; cin >> x >> y >> z;
            e[num++] = edge(x, y, z);
            e[num++] = edge(y, x, z);
        
        }
        for (int i = 1; i <= n; i++)f[i] = i;
        sort(e, e + 2*m,cmp);
        int lastw=-1, lastto=-1, lastfrom=-1;
        int res=0, flag=0;
        for (int i = 0; i < m*2; i++) {

            if (same(e[i].to, e[i].from)) {
                if (e[i].w == lastw) {
                    if ((e[i].from == lastto)&&(e[i].to!=lastfrom)) { flag = 1; break; }
                    if ((e[i].to == lastfrom) && (e[i].from != lastto)) { flag = 1; break; }
                }
                continue;
            }
            un(e[i].to, e[i].from);
            res += e[i].w;
            lastto = e[i].to;
            lastw = e[i].w;
            lastfrom = e[i].from;
        }
        if (flag)cout << "Not Unique!";
        else cout << res;
        cout << endl;
    }
}