一道圆方树模板题
推荐阅读/参考资料 圆方树学习笔记——小粉兔
题意简述
给定一张简单无向图,问有多少对三元组 (<s,c,f>) (互不相同)使得存在一条简单路径从 (s) 出发,经过 (c) 到达 (f) 。
思路
每一对固定的从起点 (s) 到终点 (f) 的 (c) 的数量显然相当于这两点间所有简单路径上的点数之和减去 $2 (s,f $ 本身 ()) ,但对于题目中的无规律图(无规律在于含有环、可能为森林等),这样的点数显然不好求,所以我们想到了圆方树。
圆方树可以做到把简单无向图转换为我们熟悉的树结构,从而进行一些树上的操作,所以我们在遇到这种图时会想到圆方树
利用差分的思想,我们将圆方树上的每个圆点权值赋为 (-1) ,每个方点的权值赋为其点双的大小,最终答案转化为:
[sum w_i,iin T
]
( (T) 为圆方树, (G) 为原图)
考虑到每个点 (i) 作为中转点 (c) ,它的贡献为以下两种情况之和:
- (s) 与 (f) 都 为它的子树中的点,此时贡献为
[2 imes sum size_j imes (size_i-size_j) imes w_i
]
- (j) 为 (i) 子树中的节点
图示为 (j=2) , (i=1) 时,红色为 (size_2) ,蓝色为 (size_1-size_2) ,相乘即为节点 (2) 作为节点 (1) 的子节点时对 (1) 的贡献。
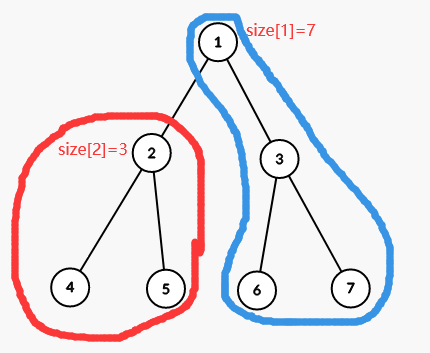
- (s,f) 有且仅有一个为 (i) 的子节点时,所有点 (j) 产生的总贡献为:
[2 imes size_i imes (num-size_i) imes w_i
]
- 其中 (num) 为圆方树总节点数。
需要注意的是: ( ext{dfs}) 遍历每个点作为中转点时,子树中的节点既可作为起点也可作为终点,所以它的贡献要乘 (2) 。
这样做的好处在于在统计贡献时不用专门区分方点和圆点,只需通过特殊点权 (w) 就可以实现统计,比较好理解。
具体实现看代码
(Code)
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N=2e5+7,M=2e5+7;//圆方树点数记得开双倍
int w[N];//点权
int n,m;
inline void read(int &x)
{
char ch=getchar();x=0;
while(ch<'0'||ch>'9') ch=getchar();
while(ch>='0'&&ch<='9') x=(x<<3)+(x<<1)+(ch^48),ch=getchar();
}
int fst[N],tot=0;
int fst1[N],tot1=0;
struct rec{int to,nxt;}e[M<<1];
struct rec1{int to,nxt;}e1[M<<1];
inline void add(int u,int v,bool o)
{
if(!o)
{
e[++tot].to=v;
e[tot].nxt=fst[u];
fst[u]=tot;
e[++tot].to=u;
e[tot].nxt=fst[v];
fst[v]=tot;
}
else
{
e1[++tot1].to=v;
e1[tot1].nxt=fst1[u];
fst1[u]=tot1;
e1[++tot1].to=u;
e1[tot1].nxt=fst1[v];
fst1[v]=tot1;
}
}
int dfn[N],low[N],st[N];
int sub=0,cnt=0,top=0,num=0;
int min(int a,int b){return a<b?a:b;}
void Tarjan(int u)//圆方树经典操作
{
dfn[u]=low[u]=++sub,st[++top]=u;
num++;
for(int i=fst[u];i;i=e[i].nxt)
{
int v=e[i].to;
if(!dfn[v])
{
Tarjan(v);
low[u]=min(low[v],low[u]);
if(low[v]==dfn[u])
{
w[++cnt]=1;//更新方点权值
while(st[top]!=v)
{
w[cnt]++;
add(cnt,st[top],1);
top--;
}
add(cnt,u,1);
top--,w[cnt]++,add(v,cnt,1);
}
}
else
low[u]=min(dfn[v],low[u]);
}
}
ll ans=0;
int size[N<<1];
void dfs(int x,int fa)
{
size[x]=(x<=n);//方点不具实际大小
for(int i=fst1[x];i;i=e1[i].nxt)
{
int y=e1[i].to;
if(y==fa) continue;
dfs(y,x);
ans+=(ll)2*(ll)size[x]*(ll)size[y]*(ll)w[x];//节点作为x子节点的贡献,注意此时的size[x]在未加上size[y]前与size[y]相乘 size[x]+=size[y];
}
ans+=(ll)2*(ll)size[x]*(ll)(num-size[x])*(ll)w[x];//子树内的节点与外部节点作为s,f的贡献
}
int main()
{
read(n),read(m);
cnt=n;
for(int i=1;i<=n;i++) w[i]=-1;
for(int i=1,x,y;i<=m;i++)
{
read(x),read(y);
add(x,y,0);
}
for(int i=1;i<=n;i++)//注意处理森林
if(!dfn[i])
{
num=0;
Tarjan(i);
--top;
dfs(i,0);
}
cout<<ans;
return 0;
}