深度学习系列（9）——node2vec算法中的alias采样介绍

1、说在前面

• Alias采样是时间复杂度为o(1)的离散采样方式
• 论文地址：http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.675.8158&rep=rep1&type=pdf

2、详细介绍

问题

　　比如一个随机事件包含四种情况，每种情况发生的概率分别为： 1/2,1/3,1/12,1/12问怎么用产生符合这个概率的采样方法。

最容易想到的方法

　　我之前有在【数学】均匀分布生成其他分布的方法中写过均匀分布生成其他分布的方法，这种方法就是产生0~1之间的一个随机数，然后看起对应到这个分布的CDF中的哪一个，就是产生的一个采样。比如落在0~ 1/2之间就是事件A，落在1/2~5/6之间就是事件B，落在5/6~11/12之间就是事件C，落在11/12~1之间就是事件D。
　　但是这样的复杂度，如果用BST树来构造上面这个的话，时间复杂度为O(logN)，有没有时间复杂度更低的方法。

一个Naive的办法

　　1. 可以像上图这样采样，将四个事件排成4列：1~4，扔两次骰子，第一次扔1~4之间的整数，决定落在哪一列。

　　2. 如上如所示，将其按照最大的那个概率进行归一化。在1步中决定好哪一列了之后，扔第二次骰子，0~1之间的任意数，如果落在了第一列上，不论第二次扔几，都采样时间A，如果落在第二列上，第二次扔超过2/3则采样失败，重新采样，如果小于2/3则采样时间B成功，以此类推。
　　3. 这样算法复杂度最好为O(1)最坏有可能无穷次，平均意义上需要采样O(N)
那怎么去改进呢？

Alias Method

　　还是如上面的那样的思路，但是如果我们不按照其中最大的值去归一化，而是按照其均值归一化。即按照1/N（这里N是情况的种数，这里四种）归一化，即为所有概率乘以N，得到如下图：

　　其总面积为N，然后可以将其分成一个1*N的长方形，如下图：

　　将前两个多出来的部分补到后面两个缺失的部分中。
　　先将1中的部分补充到4中：

　　这时如果，将1,2中多出来的部分，补充到3中，就麻烦了，因为又陷入到如果从中采样超过2个以上的事件这个问题中，所以Alias Method一定要保证：每列中最多只放两个事件
　　所以此时需要将1中的补满3中去：

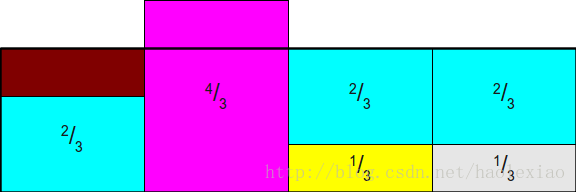
　　再将2中的补到1中：

至此整个方法大功告成

Alias Method具体算法如下：

　　1. 按照上面说的方法，将整个概率分布拉平成为一个1*N的长方形即为Alias Table，构建上面那张图之后，储存两个数组，一个里面存着第ii列对应的事件ii矩形站的面积百分比【也即其概率】，上图的话数组就为Prab[2/3, 1, 1/3, 1/3]，另一个数组里面储存着第ii列不是事件ii的另外一个事件的标号，像上图就是Alias[1 0 0 0]
2.产生两个随机数，第一个产生1~N 之间的整数i，决定落在哪一列。扔第二次骰子，0~1之间的任意数，判断其与Prab[i]大小，如果小于Prab[i]，则采样i，如果大于Prab[i]，则采样Alias[i]

3、算法实现

import numpy as np

def alias_table(prob_table):
    n = len(prob_table)
    prob_norm = np.array(prob_table) * n
    small, large = [], []
    for i, prob in enumerate(prob_norm):
        if prob < 1:
            small.append(i)
        else:
            large.append(i)

    accept, alias = [0] * n, [0] * n
    while small and large:
        small_idx, large_idx = small.pop(), large.pop()
        # 存放第i列对应的事件i的概率；
        accept[small_idx] = prob_norm[small_idx]
        # 存放不是事件i的另外事件的标号；
        alias[small_idx] = large_idx

        prob_norm[large_idx] = prob_norm[large_idx] - (1 - prob_norm[small_idx])
        if prob_norm[large_idx] < 1.0:
            small.append(large_idx)
        else:
            large.append(large_idx)

    while small:
        small_idx = small.pop()
        accept[small_idx] = 1

    while large:
        large_idx = large.pop()
        accept[large_idx] = 1
    print(accept)
    print(alias)
    return accept, alias

def alias_sample(accept, alias):
    n = len(accept)
    i = int(np.random.random() * n)
    r = np.random.random()
    if r < accept[i]:
        return i
    else:
        return alias[i]

if __name__ == '__main__':
    prob_table = [1 / 2, 1 / 3, 1 / 12, 1 / 12]
    ac, a = alias_table(prob_table)
    i = alias_sample(ac, a)
    print(i)

————————————————
版权声明：本文为CSDN博主「哈乐笑」的原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/haolexiao/article/details/65157026